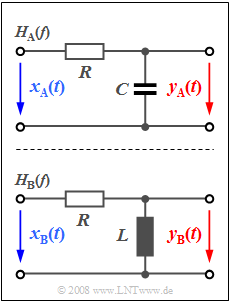
Exercise 1.1: Simple Filter Functions
A filter with the frequency response
- $$H_{\rm LP}(f) = \frac{1}{1+ {\rm j}\cdot f/f_0}$$
is described as a low-pass filter of first order. Out of it, a first order high-pass filter can be designed according to the following rule:
- $$H_{\rm HP}(f) = 1- H_{\rm LP}(f) .$$
In both cases $f_0$ represents the so-called $\text{3 dB}$–cutoff frequency.
The figure shows two two-port networks $\rm A$ and $\rm B$. The task is to clarify which of the two networks has a low-pass characteristic and which has a high-pass characteristic.
The components of circuit $\rm A$ are given as follows:
- $$R = 50 \,\, {\rm \Omega}, \hspace{0.2cm} C = 637 \,\, {\rm nF} .$$
The inductivity $L$ of circuit $\rm B$ is to be computed in subtask (6) .
Please note:
- The task belongs to the chapter System Description in Frequency Domain.
- For the subtask (4) cosine-shaped input signals are assumed. The frequency $f_x$ is variable, the power is $P_x = 10\,{\rm mW}.$
Questions
Sample solution
- The complex resistance of the capacitance $C$ is equal to $1/({\rm j}ωC)$, where $ω = 2πf$ represents the so-called angular frequency.
- The frequency response can be calculated according to the voltage divider principle:
- $$H_{\rm A}(f) = \frac{Y_{\rm A}(f)}{X_{\rm A}(f)} = \frac{1/({\rm j}\omega C)}{R+1/({\rm j}\omega C)}=\frac{1}{1+{\rm j \cdot 2\pi}\cdot f \cdot R\cdot C}.$$
- Because of $H_{\rm A}(f = 0) = 1$ this cannot be a high-pass filter; rather it is a low-pass filter.
- At low frequencies, the reactance of the capacitance is very large and $y_{\rm A}(t) ≈ x_{\rm A}(t)$ applies.
- In contrast to this, at very high frequencies, the capacitor acts like a short circuit and $y_{\rm A}(t) ≈ 0$ holds.
(2) By comparing the coefficients between $H_{\rm LP}(f)$ given in the statement of the task and $H_{\rm A}(f)$ according to subtask (1) the following is obtained:
- $$f_0 = \frac{1}{2\pi \cdot R \cdot C} = \frac{1}{2\pi \cdot{\rm 50\hspace{0.05cm} \Omega}\cdot {\rm 637 \cdot 10^{-9}\hspace{0.05cm} s/\Omega}}\hspace{0.15cm}\underline{\approx 5 \, {\rm kHz}}.$$
(3) The amplitude response is:
- $$|H_{\rm A}(f)| = \frac{1}{\sqrt{1+ (f/f_0)^2}}.$$
- For $f = f_0$ the numerical value $1/\sqrt{2}\hspace{0.1cm} \underline{≈ 0.707}$ is obtained, and
- for $f = 2f_0$ approximately the value $1/\sqrt{5}\hspace{0.1cm} \underline{≈ 0.447}$.
(4) The output power can be calculated using the following equation:
- $$P_y = P_x \cdot |H_{\rm A}(f = f_x)|^2.$$
- For $f_x = f_0$ ⇒ $P_y = P_x/2 \hspace{0.1cm} \underline{ = 5\hspace{0.1cm} {\rm mW}}$, so this results in half of the power at the output.
- In logarithmic representation, this relationship is:
- $$10 \cdot {\rm lg}\hspace{0.2cm} \frac{P_x(f_0)}{P_y(f_0)} = 3\,{\rm dB}.$$
- Accordingly, for $f_0$ the term "3dB cut-off frequency" is also common.
- For $f_x = 2f_0$, on the other hand, a smaller value is obtained: $P_y = P_x/5 \hspace{0.1cm}\underline{= 2\hspace{0.1cm} {\rm mW}}$.
(5) Analogous to subtask (1) the following holds:
- $$H_{\rm B}(f) = \frac{Y_{\rm B}(f)}{X_{\rm B}(f)} = \frac{{\rm j}\omega L}{R+{\rm j}\omega L}=\frac{{\rm j2\pi}\cdot f \cdot L/R}{1+{\rm j2\pi}\cdot f \cdot L/R}.$$
- Using the reference frequency $f_0 = R/(2πL)$ this can also be written as in the following:
- $$H_{\rm B}(f) = \frac{{\rm j}\cdot f/f_0}{1+{\rm j}\cdot f/f_0}\hspace{0.5cm}\Rightarrow \hspace{0.5cm}|H_{\rm B}(f)| = \frac{|f/f_0|}{\sqrt{1+ (f/f_0)^2}}.$$
- Hence, these numerical values are obtained:
- $$|H_{\rm B}(f = 0)| \hspace{0.15cm}\underline{= 0}, \hspace{0.5cm} |H_{\rm B}( f_0)| \hspace{0.15cm}\underline{=0.707}, \hspace{0.5cm}|H_{\rm B}(2f_0)| \hspace{0.15cm}\underline{= 0.894}, \hspace{0.5cm}|H_{\rm B}(f \rightarrow \infty)|\hspace{0.15cm}\underline{ = 1}.$$
- Therefore, the circuit $\rm B$ is a high-pass filter.
(6) According to the above definition of the reference frequency it follows that:
- $$L = \frac{R}{2\pi \cdot f_0} = \frac{{\rm 50\hspace{0.05cm} \Omega}}{2\pi \cdot{\rm 5000 \hspace{0.05cm} Hz}}= {\rm 1.59 \cdot 10^{-3}\hspace{0.05cm} \Omega s}\hspace{0.15cm}\underline{= {\rm 1.59 \hspace{0.1cm} mH}} .$$