Different binary sequences
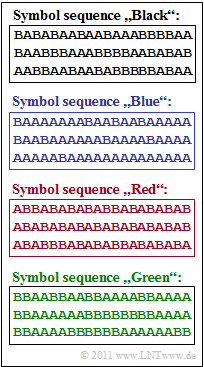
The graphic on the right shows four symbol sequences $\langle q_\nu \rangle $, each with length $N = 60$. The source symbols are $\rm A$ and $\rm B$.
- It follows directly that $H_0 = 1 \; \rm bit/symbol$ applies to the decision content of all sources considered.
- However, the symbols $\rm A$ and $\rm B$ do not occur with equal probability, but with the probabilities $p_{\rm A}$ and $p_{\rm B}$.
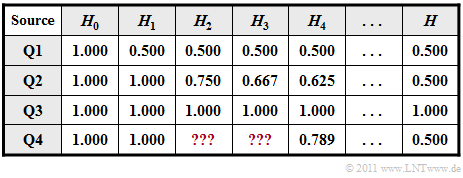
In addition to $H_0$ , the table below shows the entropy approximations
- $H_1$, based on $p_{\rm A}$ und $p_{\rm B}$ (column 2),
- $H_2$, based on two-tuples (column 3),
- $H_3$, based on three-tuples (column 4),
- $H_4$, based on four-tuples (column 5),
- the actual entropy $H$, which is obtained from $H_k$ by the boundary transition for $k \to \infty$ (last column).
The following size relations exist between these entropies: $H \le$ ... $\le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$
- What is not known is the correlation between the sources $\rm Q1$, $\rm Q2$, $\rm Q3$, $\rm Q4$ and the symbol sequences shown in the graph
(black, blue, red, green). - It is only known that source $\rm Q4$ contains a repetition code. Due to the fact that in the corresponding symbol sequence every second symbol does not lier any information, the final entrpy value is $H = 0.5 \; \rm bit/symbol$.
- In addition, the entropy approximations $H_1 = 1 \; \rm bit/symbol$ and $H_4 \approx 0.789 \; \rm bit/symbol$ are given.
Finally, the entropy approximations $H_2$ and $H_3$ are to be determined for the source $\rm Q4$ .
Source entropy and approximations in "bit/symbol"
Hints:
- This task belongs to the chapter Discrete Sources with Memory.
- For the $k$–th entropy approximation, the following holds for binary sources $(M = 2)$ with the composite probability $ p_i^{(k)}$ of a $k$–tuple:
- $$H_k = \frac{1}{k} \cdot \sum_{i=1}^{2^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_i^{(k)}} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol}) \hspace{0.05cm}.$$
Questions
Solution
(1) The black binary sequence comes from the source $\underline{\rm Q3}$,
- since the symbols are equally probable ⇒ $H_1 = H_0$, and
- there are no statistical bindings between the symbols ⇒ $H=$ ... $= H_2 = H_1$.
(2) It can be seen in the blue binary sequence that $\rm A$ occurs much more frequently than $\rm B$, so that $H_1 < H_0$ must hold.
- According to the table, only source $\underline{\rm Q1}$ fulfils this condition.
- From $H_1 = 0.5 \; \rm bit/symbol$ one can determine the symbol probabilities $p_{\rm A} = 0.89$ and $p_{\rm B} = 0.11$ .
(3) By exclusion procedure one arrives at the result $\underline{\rm Q2}$ for the red binary sequence:
- The source $\rm Q1$ belongs to the blue sequence, $\rm Q3$ to the black and $\rm Q4$ to the repetition code and thus obviously to the green symbol sequence.
- The red symbol sequence has the following properties:
- Because of $H_1 = H_0$ , the symbols are equally probable: $p_{\rm A} = p_{\rm B} = 0.5$.
- Because of $H < H_1$, there are statistical bindings within the sequence.
- This can be recognised by the fact that there are more transitions between $\rm A$ and $\rm B$ than with statistical independence.
(4) In the green symbol sequence $($source $\rm Q4)$ , the symbols $\rm A$ and $\rm B$ are equally likely:
Symbol sequences of a binary repetition code
- $$p_{\rm A} = p_{\rm B} = 0.5 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}H_1 = 1\,{\rm bit/Symbol} \hspace{0.05cm}.$$
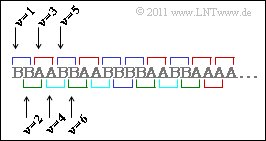
To determine $H_2$, one considers two-tuples. The composite probabilities $p_{\rm AA}$, $p_{\rm AB}$, $p_{\rm BA}$ and $p_{\rm BB}$ can be calculated from this. You can see from the sketch:
- The combinations $\rm AB$ and $\rm BA$ are only possible if a tuple starts at even $\nu$ . For the composite probabilities $p_{\rm AB}$ and $p_{\rm BA}$ then holds:
- $$p_{\rm AB} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}(\nu {\rm \hspace{0.15cm}is\hspace{0.15cm}even}) \cdot {\rm Pr}( q_{\nu} = \mathbf{A}) \cdot {\rm Pr}(q_{\nu+1} = \mathbf{B}\hspace{0.05cm} | q_{\nu} = \mathbf{A}) = {1}/{2} \cdot {1}/{2} \cdot {1}/{2} = {1}/{8} = p_{\rm BA} \hspace{0.05cm}.$$
- In contrast, for the two other combinations $\rm AA$ and $\rm BB$:
- $$p_{\rm AA} ={\rm Pr}(\nu = 1) \cdot {\rm Pr}( q_1 = \mathbf{A}) \cdot {\rm Pr}(q_{2} = \mathbf{A}\hspace{0.05cm} | q_{1} = \mathbf{A}) + {\rm Pr}(\nu=2) \cdot {\rm Pr}( q_{2} = \mathbf{A}) \cdot {\rm Pr}(q_{3} = \mathbf{A}\hspace{0.05cm} | q_{2} = \mathbf{A}) \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm}p_{\rm AA} = \frac{1}{2} \cdot \frac{1}{2} \cdot 1+ \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{3}{8} = p_{\rm BB} \hspace{0.05cm}.$$
- Here $\nu = 1$ stands for all odd indices and $\nu = 2$ for all even indices.
- This gives for the entropy approximation:
- $$H_2 = \frac{1}{2} \cdot \left [ 2 \cdot \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}\frac {8}{3} + 2 \cdot \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8)\right ] = \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}(8) - \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}(3) + \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} \underline {= 0.906 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(5) Following a similar procedure, we arrive at the composite probabilities for three-tuples
- $$p_{\rm AAA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm BBB} = 1/4 \hspace{0.05cm},\hspace{0.2cm} p_{\rm ABA} = p_{\rm BAB} = 0 \hspace{0.05cm},\hspace{0.2cm} p_{\rm AAB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABB} = p_{\rm BBA} = p_{\rm BAA} = 1/8$$
and from this to the entropy approximation
- $$H_3 = \frac{1}{3} \cdot \left [ 2 \cdot \frac{1}{4} \cdot {\rm log}_2\hspace{0.1cm}(4) + 4 \cdot \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8)\right ] = \frac{2.5}{3} \hspace{0.15cm} \underline {= 0.833 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
To calculate $H_4$ , the $16$ probabilities are as follows:
- $$p_{\rm AAAA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm BBBB} = 3/16 \hspace{0.05cm},\hspace{0.2cm} p_{\rm AABB} = p_{\rm BBAA} = 2/16 \hspace{0.05cm},$$
- $$ p_{\rm AAAB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABBA} = p_{\rm ABBB} = p_{\rm BBBA} = p_{\rm BAAB} = p_{\rm BAAA}= 1/16 \hspace{0.05cm}$$
- $$ p_{\rm AABA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABAA} = p_{\rm ABAB} = p_{\rm BBAB} = p_{\rm BABB} = p_{\rm BABA}= 0\hspace{0.05cm}.$$
It follows that:
- $$H_4= \frac{1}{4} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\left [ 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{3}{16} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.1cm}\frac{16}{3} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{1}{8} \hspace{-0.05cm}\cdot \hspace{-0.05cm}{\rm log}_2\hspace{0.1cm}(8) + 6 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{1}{16} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.1cm}(16)\right ] =\frac{\left [ 6 \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(16) - 6 \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(3) + 4 \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(8) + 6\hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(16)\right ]}{32} .$$
One can see:
- Even the approximation $H_4 = 0.789\,{\rm bit/Symbol}$ still deviates significantly from the final entropy value $H = 0.5\,{\rm bit/symbol}$ .
- The repetition code obviously cannot be modelled by a Markov source. If $\rm Q4$ were a Markov source, then the following would have to apply:
- $$H = 2 \cdot H_2 - H_1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}H_2 = 1/2 \cdot (H+H_1) = 1/2 \cdot (0.5+1) = 0.75 \,{\rm bit/Symbol}\hspace{0.05cm}.$$
