Exercise 1.4Z: Sum of Ternary Quantities

• Return to book

Sum of two ternary variables  $x$  and  $y$

Let be given the ternary random variables

$$x ∈ {–2, \ 0, +2},$$

$$y ∈ {–1, \ 0, +1}.$$

• These two ternary values each occur with equal probability. 
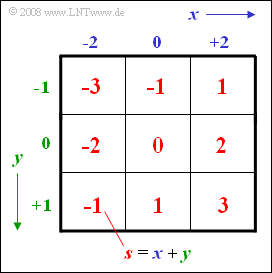
• From this,  the sum  $s = x + y$  is formed as a new random variable.
• The adjacent scheme shows that the sum  $s$  can take all integer values between  $–3$  and  $+3$ :

$$s \in \{-3, -2, -1, \ 0, +1, +2, +3\}.$$

Hints:

• The exercise belongs to the chapter  Statistical dependence and independence.

• The topic of this chapter is illustrated with examples in the  (German language)  learning video

Statistische Abhängigkeit und Unabhängigkeit   $\Rightarrow$   "Statistical dependence and independence".

Questions

1

Calculate the probability that the sum  $s$  is positive:

${\rm Pr}(s>0) \ = \ $

2

Calculate the probability that both the input  $x$  and the sum  $s$  are positive:

${\rm Pr}\big [(x>0) \cap (s>0)\big] \ = \ $

3

Calculate the conditional probability that the input variable  $x > 0$,  when  $s > 0$  holds:

${\rm Pr}(x>0\hspace{0.05cm}|\hspace{0.05cm}s>0)\ = \ $

4

Calculate the conditional probability that the sum  $s$  is positive,  when the input variable is  $x > 0$ :

${\rm Pr}(s>0\hspace{0.05cm}|\hspace{0.05cm}x>0)\ = \ $

Solution

Solution

Ternary variables in the Venn diagram

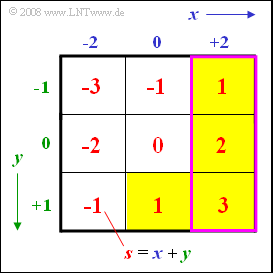
In the adjacent graph

• the three fields belonging to the event  $\big[x > 0\big]$  are outlined in purple,
• the fields for  $\big[ s > 0\big]$  are highlighted in yellow.

All sought probabilities can be determined here with the help of the classical definition.

(1)  This event is marked by the fields with yellow background:

$$\rm Pr (\it s > \rm 0) = \rm 4/9 \hspace{0.15cm}\underline { \approx \rm 0.444}.$$

(2)  The following facts hold here:

$$\rm Pr \big[(\it x > \rm 0) \cap (\it s>\rm 0) \big ] = \rm Pr(\it x > \rm 0) =\rm 3/9\hspace{0.15cm}\underline { \approx \rm 0.333}.$$

(3)  Using the results of subtasks  (1)  and  (2),  it follows:

$$\rm Pr \big[(\it x > \rm 0) \hspace{0.05cm}| \hspace{0.05cm} (\it s > \rm 0)\big] = \frac{{\rm Pr} [(\it x > \rm 0) \cap (\it s > \rm 0)]}{{\rm Pr}(\it s > \rm 0)}= \frac{3/9}{4/9}\hspace{0.15cm}\underline {= 0.75}.$$

(4)  Analogous to subtask  (3)  now holds:

$$\rm Pr(\it s > \rm 0 \hspace{0.05cm} | \hspace{0.05cm} \it x > \rm 0)=\frac{Pr \big[(\it x > \rm 0) \cap (\it s > \rm 0) \big]}{Pr(\it x >\rm 0)}=\rm \frac{3/9}{3/9}\hspace{0.15cm}\underline {= 1}.$$