Exercise 2.4: GF(2 to the Power of 2) Representation Forms

• Return to book

Three representation forms for  ${\rm GF}(2^2)$

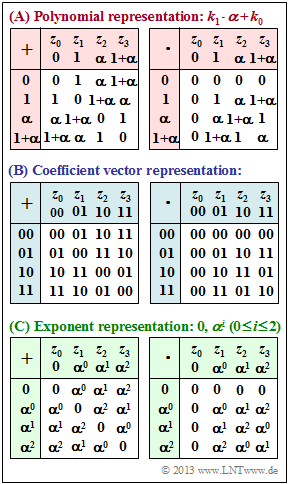
Opposite you can see the addition table as well as the multiplication table for the extension field  $\rm GF(2^2)$  in three different variants:

• the  polynomial representation,

• the  coefficient vector representation,

• the  exponent representation.

Hints:

• The exercise refers to the chapter  "Extension fields".

• All necessary information about  ${\rm GF}(2^2)$  can be found on the  "first page"  of this chapter.

• In subtask  (4)  the following expressions are considered:

$$A = z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3,$$

$$B = (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3).$$

Questions

1

What characteristics can be recognized from the polynomial representation?

	The elements  "$\alpha$"  and  "$1 + \alpha$"  are neither  $0$  nor  $1$.
	The arithmetic operations are performed modulo  $2$.
	The arithmetic operations are performed modulo  $4$.
	One recognizes the result   $\alpha^2 + \alpha + 1 = 0$   from the addition table.
	One recognizes the result   $\alpha^2 + \alpha + 1 = 0$   from the multiplication table.

2

What is the relationship between the coefficient vector and the polynomial representation?
Let  $k_0 ∈ \{0, \, 1\}$  and  $k_1 ∈ \{0, \, 1\}$ hold.

	"$(k_0 \ k_1)"$  refers to the element  "$k_1 \cdot \alpha + k_0$".
	"$(k_1 \ k_0)$"  refers to the element  "$k_1 \cdot \alpha + k_0$".
	There is no relationship between the two representations.

3

How are polynomial and exponent representation related?

	No connections can be seen.
	The elements  "$0, \ 1$"  and  "$\alpha$"  are the same in both representations.
	The element  "$1 + \alpha$"  is  "$\alpha^2$"  in the exponent representation.
	The element  "$\alpha^2$"  of the exponent representation stands for  "$\alpha \cdot (1 + \alpha)$".

4

Calculate the expressions  $A$  and  $B$  according to these three forms of representation.  Which statements are true?

	It holds  $A = z_0$,
	It holds  $A = z_2$,
	It holds  $B = z_1$,
	It holds  $B = z_3$.

Solution

Solution

(1)  The  proposed solutions 1, 2 and 5  are applicable.  Justification:

• If  $\alpha = 0$  or  $\alpha = 1$,  the pseudo element  $\alpha$  would be indistinguishable from the other two  ${\rm GF}(2)$  elements  $0$  and  $1$.

• The modulo-2 calculation can be recognized from the addition table.  For example,  $1 + 1 = 0, \ \alpha + \alpha = 0, \ (1 + \alpha) + (1 + \alpha) = 0$, etc.
• From the multiplication table we see that  $\alpha^2 = \alpha \cdot \alpha = 1 + \alpha$  holds  $($3rd row,  3rd column$)$.  Thus also

$$\alpha^2 + \alpha + 1 = 0.$$

(2)  Correct is the  solution suggestion 2.  Thus

• "$01$"  for the element  "$1$"  and

• "$10$"  for the element  "$\alpha$".

(3)  Correct are the  solutions 2 and 3:

• It is true that  $\alpha^0 = 1$  and  $\alpha^1 = \alpha$.

• For the underlying polynomial  $p(x) = x^2 + x + 1$,  it follows further from  $p(\alpha) = 0$:

$$\alpha^2 +\alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^2 =\alpha + 1 \hspace{0.05cm}.$$

(4)  According to the tables of polynomial representation holds:

$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = \alpha \cdot \alpha + \alpha \cdot (1+\alpha) + (1+\alpha) \cdot (1+\alpha) = (1+\alpha) + (1) + (\alpha) = 0 = z_0 \hspace{0.05cm},$$

$$B \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = (0 + 1 + \alpha) \cdot (0 + 1 + 1+ \alpha) = (1+\alpha) \cdot \alpha = 1 = z_1 \hspace{0.05cm}.$$

• Therefore,  the  proposed solutions 1 and 2  are correct.

• The same results are obtained with the coefficient vector representation:

$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = (10) \cdot (10) + (10) \cdot (11) + (11) \cdot (11) = (11) + (01) + (10) = (00) = 0 = z_0 \hspace{0.05cm},$$

$$B \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = [(00) + (01) + (10)] \cdot [(00) + (01) + (11)] =(11) \cdot (10) = (01) = z_1 \hspace{0.05cm}.$$

• And finally with the exponent representation:

$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = \alpha^1 \cdot \alpha^1 + \alpha^1 \cdot \alpha^2 + \alpha^2 \cdot \alpha^2 = \alpha^2 + \alpha^3 + \alpha^4 = \alpha^2 + \alpha^0 + \alpha^1 = 0 = z_0 \hspace{0.05cm},$$

$$B \hspace{-0.15cm} \ = \ \hspace{-0.15cm}(z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = [0 + \alpha^0 + \alpha^1] \cdot [0 + \alpha^0 + \alpha^2] = \alpha^2 \cdot \alpha^1 = \alpha^3 = \alpha^0 = z_1 \hspace{0.05cm}.$$