Exercise 3.7: Bit Error Rate (BER)

• Return to book

To illustrate the bit error rate

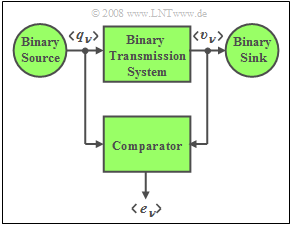
We consider a binary transmission system with

• the source symbol sequence  $\langle q_\nu \rangle$,  and
• the sink symbol sequence  $\langle v_\nu \rangle$.

If the sink symbol  $v_\nu$  and source symbol  $q_\nu$  do not match,  there is a  "bit error"   ⇒   $e_\nu = 1$.  Otherwise  $e_\nu = 0$  holds.

$\rm (A)$  The most important evaluation criterion of such a digital system is the  Bit Error Probability:

• With the expected value  ${\rm E}\big[\text{ ...} \big]$  this is defined as follows:

$$\it p_{\rm B} = \rm E\big[\rm Pr(\it v_{\nu} \ne q_{\nu} \rm )\big]=\rm E\big[\rm Pr(\it e_{\nu}=\rm 1)\big]=\lim_{{\it N}\to\infty}\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N}\rm Pr(\it e_{\nu}=\rm 1).$$

• The right part of this equation describes a time averaging; this must always be applied to time-varying channels.
• If the error probability is the same for all symbols  (which is assumed here),  the above equation can be simplified:

$$\it p_{\rm B} = \rm E\big[\rm Pr(\it e_{\nu}=\rm 1)\big]=\rm E\big[\it e_{\nu} \rm \big].$$

• The bit error probability is an  "a priori parameter",  so it allows a prediction for the expected result.

$\rm (B)$  For the metrological determination of the transmission quality or for a system simulation,  it is necessary to rely on the  Bit Error Rate  $\rm (BER)$:

• The bit error rate is an  "a posteriori parameter"  derived from a performed statistical experiment as a  relative frequency.

$$h_{\rm B}=\frac{n_{\rm B}}{N}=\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N} e_{\nu}.$$

• $n_{\rm B}$  indicates the number of bit errors occurred when a total of  $N$  binary symbols  ("bits")  were transmitted.
• In the limiting case  $N \to \infty$  the relative frequency  $h_{\rm B}$  coincides with the probability  $p_{\rm B}$.  Here now the question shall be clarified,  which statistical uncertainty has to be expected with finite  $N$.

Hints:

• The exercise belongs to the chapter  Gaussian random variables.
• Solve this exercise as far as possible in general.  Use the parameter values  $p_{\rm B} = 10^{-3}$  and  $N = 10^{5}$ for control input.
• The following are some values of the so-called  "Q-function":

$$\rm Q(\rm 1.00)=\rm 0.159,\hspace{0.5cm}\rm Q(\rm 1.65)=\rm 0.050,\hspace{0.5cm}\rm Q(\rm 1.96)=\rm 0.025,\hspace{0.5cm}\rm Q(\rm 2.59)=\rm 0.005.$$

Questions

1

Which of the following statements are true?

	For  $n_{\rm B}$  all values  $(0$, ... , $N)$  are equally likely.
	The random variable  $n_{\rm B}$  is binomially distributed.
	With  $p_{\rm B} = 10^{-3}$  and  $N = 10^{5}$  we get  ${\rm E}\big[n_{\rm B}\big] = 100$.

2

How large is the standard deviation of the random variable  $n_{\rm B}$  with  $p_{\rm B} = 10^{-3}$  and  $N = 10^{5}$?

$\sigma_{n{\rm B}} \ = \ $

3

What values can the bit error rate  $h_{\rm B}$  take?  Show that the linear mean  $m_{h{\rm B}}$  of this random variable is equal to the bit error probability  $p_{\rm B}$  What is its standard deviation?

$\sigma_{h{\rm B}} \ = \ $

4

Under certain conditions,  a binomially distributed random variable can be approximated by a Gaussian distribution
with equal mean  $(m_{h{\rm B}})$  and equal standard deviation  $(\sigma_{h{\rm B}})$.  Which statement is true?

	${\rm Pr}(\hspace{0.05cm}|\hspace{0.05cm}h_{\rm B} - p_{\rm B}\hspace{0.05cm}| \le \varepsilon)=1- 2\cdot \rm Q({\varepsilon}/{\sigma_{\it h}{\rm B}}).$
	${\rm Pr}(\hspace{0.05cm}|\hspace{0.05cm}h_{\rm B} - p_{\rm B}\hspace{0.05cm}| \le \varepsilon)=1- \rm Q({\varepsilon}/{2\cdot \sigma_{\it h}{\rm B}}).$

5

For abbreviation,  we use the confidence level  $p_\varepsilon = {\rm Pr}(\hspace{0.05cm}|\hspace{0.05cm}h_{\rm B} - p_{\rm B}\hspace{0.05cm}| \le \varepsilon)$.   Which  $p_\varepsilon$  results with  $\varepsilon = 10^{-4}$,   $p_{\rm B} = 10^{-3}$  and  $N = 10^{5}$ ?

$p_\varepsilon \ = \ $

6

Let the argument of the Q-function be  $\alpha$.  What is the minimum value of  $\alpha$  that must be chosen for the confidence level  $p_\varepsilon = 95\%$ ?

$\alpha_{\rm min} \ = \ $

7

It still holds  $p_{\rm B} = 10^{-3}$  and  $p_\varepsilon = 95\%$.   Over how many symbols  $(N_\text{min})$  must be averaged at least,
so that the determined bit error rate lies in the range between  $0. 9 \cdot 10^{-3}$  and  $1.1 \cdot 10^{-3}$  $(\varepsilon = 10^{-4}, \ \text{10% of its nominal value)}$ ?

$N_\text{min} \ = \ $

Solution

Solution

(1)  The  last two statements  are true:

• Relative to the random variable  $n_{\rm B}$  there is the classical case of a binomial distribution.
• The sum over  $N$  binary random variables is formed.  The possible values of  $n_{\rm B}$  thus lie between  $0$  and  $N$.
• The linear mean gives   $m_{n{\rm B}}=p_{\rm B}\cdot N=\rm 10^{-3}\cdot 10^{5}=\rm 100.$

(2)  Für the standard deviation of the binomial distribution holds with good approximation:

$$\sigma_{n{\rm B}}=\sqrt{N\cdot p_{\rm B}\cdot (\rm 1- \it p_{\rm B}{\rm )}} \hspace{0.15cm}\underline{\approx 10}.$$

(3)  Possible values of  $h_{\rm B}$  are all integer multiples of  $1/N$.  These all lie between  $0$  and  $1$.

• For the mean value,  one obtains:

$$m_{h{\rm B}}=m_{n{\rm B}}/N=p_{\rm B} = 10^{-3}.$$

• The standard deviation results in

$$\sigma_{h{\rm B}}=\frac{\sigma_{n{\rm B}}}{N}=\sqrt{\frac{ p_{\rm B}\cdot (\rm 1- \it p_{\rm B}{\rm )}}{N}}\hspace{0.15cm}\underline{\approx \rm 0.0001}.$$

(4)  Correct is  the first proposition.  It holds:

$${\rm Pr}(h_{\rm B} > p_{\rm B} + \varepsilon)=\rm Q({\it\varepsilon}/{\it\sigma_{h{\rm B}}}),$$

$$\rm Pr(\it h_{\rm B} < p_{\rm B} - \varepsilon {\rm )}=\rm Q(\it{\varepsilon}/{\sigma_{h{\rm B}}}{\rm )}$$

$$\Rightarrow \hspace{0.5cm}\rm Pr(\it |h_{\rm B} - p_{\rm B}| \le \varepsilon \rm )=\rm 1-\rm 2\cdot \rm Q({\it \varepsilon}/{\it \sigma_{h{\rm B}}}).$$

(5)  One obtains with the numerical values  $\varepsilon = \sigma_{h{\rm B}} = 10^{-4}$:

$$p_{\varepsilon}=\rm 1-\rm 2\cdot \rm Q(\frac{\rm 10^{\rm -4}}{\rm 10^{\rm -4}} {\rm )}=\rm 1-\rm 2\cdot\rm Q(\rm 1)\hspace{0.15cm}\underline{\approx\rm 0.684}.$$

In words:   If one determines the bit error rate by simulation over  $10^5$  symbols,  with a confidence level of  $\underline{68.4\%}$ 
one obtains a value between  $0.9 \cdot 10^{-3}$  and  $1.1 \cdot 10^{-3}$,  if  $p_{\rm B} = 10^{-3}$.

(6)  From the relation  $p_{\varepsilon}=\rm 1-\rm 2\cdot {\rm Q}(\alpha) = 0.95$  it follows directly:

$$\alpha_{\rm min}=\rm Q^{\rm -1}\Big(\frac{\rm 1-\it p_{\varepsilon}}{\rm 2}\Big)=\rm Q^{\rm -1}(\rm 0.025)\hspace{0.15cm}\underline{=\rm 1.96}\hspace{0.15cm}{\approx\rm 2}.$$

(7)  It must  $\alpha = \varepsilon/\sigma_{h{\rm B}}$.  With the result of the subtask  (2)  then follows:

$$\frac{\varepsilon}{\sqrt{p_{\rm B}\cdot(\rm 1-\it p_{\rm B})/N}}\ge {\rm 2} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} N\ge \frac{\rm 4\cdot \it p_{\rm B}\cdot(\rm 1-\it p_{\rm B})}{\varepsilon^{\rm 2}}\approx \frac{\rm 4\cdot 10^{-3}}{10^{-8}}\hspace{0.15cm}\underline{=\rm 400\hspace{0.08cm}000}.$$