Exercise 4.11Z: OOK and BPSK once again

• Return to book

Error probabilities of On–Off Keying and Binary Phase Shift Keying

The error probabilities  $p_{\rm S}$  of the digital modulation methods "On–Off Keying"  $\rm (OOK)$  and  "Binary Phase Shift Keying"  $\rm (BPSK)$  are given here without derivation. 

For example,  one obtains with the so-called Q-function

$${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\cdot \int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u$$

for the AWGN channel – identified by  $E_{\rm S}/N_0$  – and other optimal conditions  (e.g. coherent demodulation)

• for On–Off Keying,  often also called  "Amplitude Shift Keying"  $\rm (2–ASK)$:

$$p_{\rm S} = {\rm Q}\left ( \sqrt{{E_{\rm S}}/{N_0 }} \hspace{0.1cm}\right ) \hspace{0.05cm},$$

• for Binary Phase Shift Keying:

$$p_{\rm S} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm S}}/{N_0 }} \hspace{0.1cm}\right ) \hspace{0.05cm}.$$

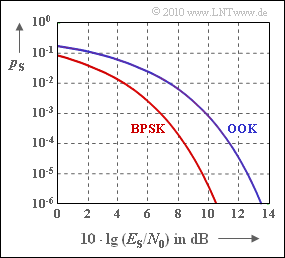
These symbol error probabilities  (at the same time the bit error probabilities)  are shown in the graph.

For example,  for  $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 \ \rm dB$  one obtains according to the exact functions:

$$p_{\rm S} = 7.83 \cdot 10^{-4}\,\,{\rm (OOK)}\hspace{0.05cm},$$

$$p_{\rm S} = 3.87 \cdot 10^{-6}\,\,{\rm (BPSK)}\hspace{0.05cm}.$$

In order to achieve  $p_{\rm S} = 10^{\rm -5}$  with BPSK,  $10 \cdot {\rm lg} \, E_{\rm S}/N_0 ≥ 9.6 \ \rm dB$  must hold.

Notes:

• The exercise belongs to the chapter  "Carrier Frequency Systems with Coherent Demodulation".

• You can also find the derivations in the chapter  "Linear Digital Modulation – Coherent Demodulation".

• For the complementary Gaussian error function, use the following approximation  (upper bound):

$${\rm Q}(x) \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$

Questions

1

Calculate the  OOK  symbol error probability for  $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 \ \rm dB$  using the upper bound.

$p_{\rm S}\ = \ $ $\ \cdot 10^{\rm –5}$

2

What is the  BPSK  symbol error probability for  $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 \ \rm dB$?

$p_{\rm S}\ = \ $ $\ \cdot 10^{\rm –5}$

3

For  OOK,  give the minimum value of  $E_{\rm S}/N_0$  $($in $\rm dB)$  required for  $p_{\rm S} = 10^{\rm -5}$.

${\rm Minimum} \big[10 \cdot {\rm lg} \, E_{\rm S}/N_0 \big ] \ = \ $ $\ \rm dB$

Solution

Solution

(1)  From  $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 \ \rm dB$  follows  $E_{\rm S}/N_0 = 10$  and thus

$$p_{\rm S} = {\rm Q}\left ( \sqrt{10} \right ) \approx \frac{\rm 1}{\sqrt{\rm 20\pi} }\cdot \rm e^{-5 } \underline{=85 \cdot 10^{-5}}\hspace{0.05cm}.$$

• The actual value according to the data section is  $78.3 \cdot 10^{\rm -5}$.

• So the given equation is actually an upper bound for  ${\rm Q}(x)$.

• The relative error when using this approximation instead of the exact function  ${\rm Q}(x)$  is in this case less than  $10\%$.

(2)  For BPSK,  the corresponding equation is:

$$p_{\rm S} = {\rm Q}\left ( \sqrt{20} \right ) \approx \frac{\rm 1}{\sqrt{\rm 40\pi} }\cdot \rm e^{-10 } \underline{=0.405 \cdot 10^{-5}}\hspace{0.05cm}.$$

• Now the relative error using the approximation is only  $5\%$.

• In general:  The smaller the error probability, the better the approximation.

(3)  According to the specification,  a (logarithmic) value of  $9.6 \ \rm dB$  is required for BPSK.

• With the OOK,  the logarithmic value must be increased by about  $3 \ \rm dB$ ⇒ $10 \cdot {\rm lg} \, E_{\rm S}/N_0 \ \underline {\approx 12.6 \ \rm dB}$.