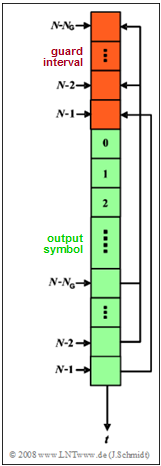
Exercise 5.8Z: Cyclic Prefix and Guard Interval
In this exercise, we assume an $\rm OFDM$ system with $N = 8$ carriers and cyclic prefix. Let the subcarrier spacing be $f_0 = 4 \ \rm kHz$ ⇒ basic symbol duration: $T=1/f_0$. The diagram shows the principle of the cyclic prefix.
- Transmission is via a two-way channel, with both paths delayed. The channel impulse response is thus with $τ_1 = \ \rm 50 µs$ and $τ_2 = 125\ \rm µs$:
- $$ h(t) = h_1 \cdot \delta (t- \tau_1) + h_2 \cdot \delta (t- \tau_2).$$
- However, the use of such a cyclic prefix decreases the bandwidth efficiency $($ratio of symbol rate to bandwidth$)$ by a factor of
- $$ \beta = \frac{1}{{1 + T_{\rm{G}} /T}} $$
- and leads also to a reduction of the signal-to-noise ratio by this value $\beta$ as well.
- However, a prerequisite for the validity of the SNR loss given here is that the impulse responses $g_{\rm S}(t)$ and $g_{\rm E}(t)$ of the transmit filter (German: "Sendefilter" ⇒ subscript: "S") and the receive filter (German: "Empfangsfilter" ⇒ subscript: "E") are matched to the symbol duration $T$ $($matched–filter approach$)$.
Notes:
- The exercise belongs to the chapter Implementation of OFDM Systems.
- Reference is made in particular to the pages Cyclic Prefix and OFDM system with cyclic prefix.
Questions
Solution
- $$ T = {1}/{f_0} \hspace{0.15cm}\underline {= 250\,\,{\rm µ s}}.$$
(2) To avoid interference, the duration $T_{\rm G}$ of the guard interval should be at least as long as the maximum channel delay $($here: $τ_2 = 125\ \rm µ s)$:
- $$ T_{\rm G} \hspace{0.15cm}\underline {= 125\,\,{\rm µ s}}.$$
(3) Thus, for the frame duration:
- $$ T_{\rm{R}} = T + T_{\rm G}\hspace{0.15cm}\underline {= 375\,\,{\rm µ s}}.$$
(4) Solution 2 is correct:
- Only intersymbol interference $\rm (ISI)$ can be avoided by a guard gap of suitable length.
- The gap duration $T_{\rm G}$ must be chosen so large that the current symbol is not affected by the predecessor symbol.
- In the present example, it must be $T_{\rm G}≥ 125\ \rm µ s$.
(5) Both solutions are applicable:
- A cyclic prefix of suitable length also suppresses intercarrier interference $\rm (ICI)$.
- This ensures that a complete and undistorted oscillation occurs for all carriers within the basic symbol duration $T$, even if other carriers are active.
(6) The number of samples within the basic symbol is equal to the number of carriers ⇒ $\underline{N=8}$.
- Because of $T_{\rm G}= T/2$ , $N_{\rm G}\hspace{0.15cm}\underline {= 4}$ and thus $N_{\rm R} = N + N_{\rm G}\hspace{0.15cm}\underline {= 12}$ holds.
(7) Assigning the coefficient "-1" to the first carrier $($frequency $f_0)$ results in the samples
- $$d_0 = -1, \hspace{0.3cm}d_1 = -0.707 - {\rm j} \cdot 0.707, \hspace{0.3cm}d_2 = -{\rm j} ,\hspace{0.3cm} d_3 = +0.707 -{\rm j} \cdot 0.707, $$
- $$d_4 = +1, \hspace{0.3cm}d_5 = +0.707 + {\rm j} \cdot 0.707, \hspace{0.3cm}d_6 = +{\rm j} ,\hspace{0.3cm} d_7 = -0.707 +{\rm j} \cdot 0.707. $$
- The cyclic expansion provides the additional samples $d_{-1} = d_7$, $d_{-2} = d_6$, $d_{-3} = d_5$ and $d_{-4} = d_4$:
- $$\underline{{\rm Re}[d_{-1}] = -0.707,\hspace{0.3cm}{\rm Im}[d_{-1}] = +0.707,\hspace{0.3cm}{\rm Re}[d_{-2}] = 0,\hspace{0.3cm} {\rm Im}[d_{-2}] = 1},$$
- $$\underline{{\rm Re}[d_{-3}] = +0.707,\hspace{0.3cm}{\rm Im}[d_{-3}] = +0.707,\hspace{0.3cm}{\rm Re}[d_{-4}] = 1,\hspace{0.3cm} {\rm Im}\{d_{-4}] = 0}.$$
(8) According to the given equation, the bandwidth efficiency is equal to
- $$\beta = \frac{1}{1 + {T_{\rm{G}}}/{T}} = \frac{1}{1 + ({125\,\,{\rm \mu s}})/({250\,\,{\rm \mu s}})} \hspace{0.15cm}\underline {= 0.667}.$$
(9) The bandwidth efficiency $β = 2/3$ results in an SNR loss of
- $$10 \cdot {\rm{lg}}\hspace{0.04cm}\Delta \rho = 10 \cdot {\rm{lg}}\hspace{0.04cm}(\beta) \hspace{0.15cm}\underline {\approx1.76\,\,{\rm{dB}}}.$$