Exercise 4.12: Root-Nyquist Systems
In "quadrature amplitude modulation" (QAM) systems, the "root-Nyquist variant" is often chosen (which gets its name from the spectral range) instead of a rectangular basic transmission pulse. The reason for this is the significantly smaller bandwidth.
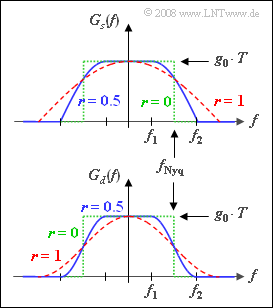
- In this case, the basic detection pulse gd(t) satisfies the first Nyquist criterion, since Gd(f) is point-symmetric about the so-called "Nyquist frequency" fNyq=1/T .
- Gd(f) is a raised-cosine spectrum, where the rolloff factor r can take values from 0 to 1 (including these limits).
Furthermore, the following holds for the Nyquist frequency response:
- When |f|<f1=fNyq·(1–r) ⇒ Gd(f) is constant and equal to g0·T.
- At frequencies greater than f2=fNyq·(1+r) ⇒ Gd(f) has no components.
- In between, the slope is cosine.
The optimization of digital communication systems requires that the receiver frequency response HE(f) should be of the same shape as the transmission spectrum Gs(f) .
To obtain dimensionally correct spectral functions for this task and the graph, it is assumed that
- Gs(f)=√g0⋅T⋅Gd(f),
- HE(f)=1g0⋅T⋅Gs(f).
The top graph shows the transmission spectrum Gs(f) for the rolloff factors
- r=0 (green dotted rectangle),
- r=0.5 (blue solid curve),
- r=1 (red dashed curve).
Below, the spectrum Gd(f) of the basic detection pulse before the decider is shown in the same colors.
- The associated pulse gd(t) is a Nyquist pulse for all valid rolloff factors (0≤r≤1) as opposed to the basic transmission pulse gs(t).
- For this, the following equation is given in the literature - for example in [Kam04] :
- gs(t)=g0⋅4rt/T⋅cos[π⋅(1+r)⋅t/T]+sin[π⋅(1−r)⋅t/T][1−(4rt/T)2]⋅π⋅t/T.
Hints:
- This exercise belongs to the chapter "Quadrature Amplitude Modulation".
- Particular reference is made to the page "Nyquist and Root-Nyquist systems" in this chapter.
- Further useful informations can be found in the chapter Properties of Nyquist Systems in the book "Digital Signal Transmission".
- [Kam04] refers to the textbook "Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004".
- Energies are to be specified in V2s; they thus refer to the reference resistance R=1 Ω.
Questions
Solution
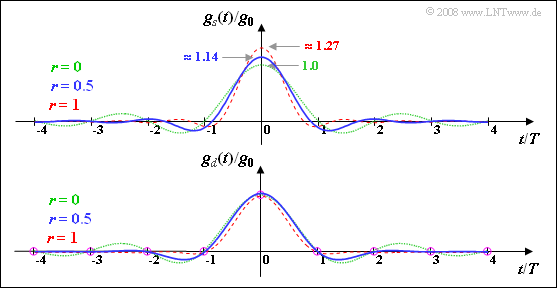
- gs(t)=g0⋅sin(π⋅t/T)π⋅t/T=g0⋅sinc(t/T).
- At time t=0, sinc(t/T)=g0:
- gs(t)=1.0_⋅g0.
(2) When r=1, the given equation simplies as follows:
- gs(t)=4⋅g0π⋅cos(2π⋅t/T)[1−(4t/T)2]⇒gs(t=0)=4⋅g0π=1.273_⋅g0.
(3) The last answer is correct:
- Zero intercepts are only possible for r=1 if the cosine function in the numerator is zero, that is, for all integer values of k:
- 2π⋅t/T=π/2+k⋅π⇒t=±0.25T,±0.75T,±1.25T,...
- However, only the last answer is correct, since the zero values at ±0.25T are cancelled by the zero in the denominator.
- Applying de l'Hospital's rule yields gs(t=±0.25T)=g0.
(4) With r=0.5 and the shortcut x=t/T, one gets:
- gs(x)=g0π⋅2⋅x⋅cos(1.5π⋅x)+sin(0.5π⋅x)(1−4⋅x2)⋅x.
- For the calculation at time t=0, de l'Hospital's rule must be applied.
- The derivatives of the numerator and denominator give:
- Z′(x)=2⋅cos(1.5π⋅x)−3π⋅x⋅sin(1.5π⋅x)+0.5π⋅cos(0.5π⋅x),
- N′(x)=(1−4⋅x2)−8⋅x2.
- The two boundary transitions for x→0 yield:
- limx→0Z′(x)=2+π/2,limx→0N′(x)=1.
- Thus, for the signal amplitude at time t=0:
- gs(t=0)=g0π⋅(2+π/2)=g0⋅(0.5+2/π)=1.137_⋅g0.
Here, the graph illustrates the results calculated again:
- gd(t) is a Nyquist pulse, meaning that it has zero crossings at least at all multiples of the symbol duration T (and possibly others depending on the rolloff factor).
- On the other hand, the pulse gs(t) does not satisfy the Nyquist criterion. Moreover, from this plot one can once again see that for r≠0 the pulse amplitude gs(t=0) is always larger than g0.
(5) The last answer is correct (the first answer is ruled out from the results in questions (2) and (4) ). The validity of the lower bound g0 and the upper bound 4g0/π can be proved as follows:
- The pulse amplitude gs(t=0) is generally equal to the area under the spectral function Gs(f).
- The smallest area is obtained for r=0. Here, Gs(f)=g0·T is in the range |f|<±1/(2T). Thus, the area is equal to g0.
- The largest area is obtained for r=1. Here, Gs(f) extends to the range ±1/T and has a cosine shape.
- The result gs(t=0)=4g0/π was already calculated in question (3) . Though it still holds that:
- gs(t=0)=2⋅g0⋅∫1/T0cos(π2⋅f⋅T)df=4g0π⋅∫π/20cos(x)dx=4g0/π⋅[sin(π/2)−sin(0)]=4g0/π.
(6) The energy of the basic transmission pulse gs(t) can be found in the time or frequency domain according to Parseval's theorem:
- Egs=∫+∞−∞[gs(t)]2dt=∫+∞−∞|Gs(f)|2df.
- From the equations and graph on the exercise page, we can see that |Gs(f)|2 has the same shape as Gd(f), but the height is now (g0·T)2 instead of g0·T:
- Egs=∫+∞−∞|Gs(f)|2df=g20⋅T2g0⋅T⋅∫+∞−∞Gd(f)df.
- Due to the Nyquist form of Gd(f), it holds independently of r:
- ∫+∞−∞Gd(f)df=g0.
- Thus, the pulse energy is also independent of r, so it is also valid for r=0 and r=1. In both cases, Egs=1.0_·g20·T.