Processing math: 100%

Different Entropy Measures of Two-Dimensional Random Variables

From LNTwww

  1. Information Theory
  2. Mutual Information Between Two Discrete Random Variables
  3. Different Entropy Measures of Two-Dimensional Random Variables


Definition of entropy using supp(PXY)


We briefly summarize the results of the last chapter again, assuming the two-dimensional random variable  XY  with the probability mass function  PXY(X, Y) .  At the same time we use the notation

supp(PXY)={(x, y)∈XY,wherePXY(X, Y)≠0};

Summarizing the last chapter:  With this subset  supp(PXY)⊂PXY,  the following holds for

  • the  »joint entropy« :
H(XY)=E[log21PXY(X,Y)]=∑(x,y)∈supp(PXY)PXY(x,y)⋅log21PXY(x,y).
  • the  »entropies of the one-dimensional random variables«  X  and  Y:
H(X)=E[log21PX(X)]=∑x∈supp(PX)PX(x)⋅log21PX(x),
H(Y)=E[log21PY(Y)]=∑y∈supp(PY)PY(y)⋅log21PY(y).


Example 1:  We refer again to the examples on the  joint probability and joint entropy  in the last chapter. 

For the two-dimensional probability mass function  PRB(R,B)  in  Example 5  with the parameters

  • R   ⇒   points of the red cube,
  • B   ⇒   points of the blue cube,


the sets  PRB  and  supp(PRB)  are identical.  Here, all  62=36  squares are occupied by non-zero values.

For the two-dimensional probability mass function  PRS(R,S)  in  Example 6  with the parameters

  • R   ⇒   points of the red cube,
  • S=R+B   ⇒   sum of both cubes,


there are  6·11=66 squares, many of which, however, are empty, i.e. stand for the probability  "0" .

  • The subset  supp(PRS) , on the other hand, contains only the  36  shaded squares with non-zero probabilities.
  • The entropy remains the same no matter whether one averages over all elements of  PRS  or only over the elements of   supp(PRS)  since for  x→0  the limit is  x·log2(1/x)=0.


Conditional probability and conditional entropy


In the book  "Theory of Stochastic Signals"  the following   conditional probabilities  were given for the case of two events  X  and  Y  ⇒   »Bayes' theorem«:

Pr(X∣Y)=Pr(X∩Y)Pr(Y),Pr(Y∣X)=Pr(X∩Y)Pr(X).

Applied to probability mass functions, one thus obtains:

PX∣Y(X∣Y)=PXY(X,Y)PY(Y),PY∣X(Y∣X)=PXY(X,Y)PX(X).

Analogous to the  joint entropy  H(XY) , the following entropy functions can be derived here:

Definitions: 

  • The  »conditional entropy« of the random variable  X  under condition  Y  is:
H(X∣Y)=E[log21PX∣Y(X∣Y)]=∑(x,y)∈supp(PXY)PXY(x,y)⋅log21PX∣Y(x∣y)=∑(x,y)∈supp(PXY)PXY(x,y)⋅log2PY(y)PXY(x,y).
  • Similarly, for the  »second conditional entropy« we obtain:
H(Y∣X)=E[log21PY∣X(Y∣X)]=∑(x,y)∈supp(PXY)PXY(x,y)⋅log21PY∣X(y∣x)=∑(x,y)∈supp(PXY)PXY(x,y)⋅log2PX(x)PXY(x,y).


In the argument of the logarithm function there is always a conditional probability function   ⇒   PX|Y(·)  or  PY|X(·)  resp.,  while the joint probability   ⇒   PXY(·) is needed for the expectation value formation.

For the conditional entropies, there are the following limitations:

  • Both  H(X|Y)  and  H(Y|X)  are always greater than or equal to zero.  From  H(X|Y)=0  it follows directly  H(Y|X)=0. 
    Both are only possible for   disjoint sets  X  and  Y.
  • H(X|Y)≤H(X)  and  H(Y|X)≤H(Y) always apply.  These statements are plausible if one realizes that one can also use  "uncertainty"  synonymously for  "entropy".  For:   The uncertainty with respect to the quantity  X  cannot be increased by knowing  Y. 
  • Except in the case of statistical independence   ⇒   H(X|Y)=H(X) ,   H(X|Y)<H(X) always holds.  Because of  H(X)≤H(XY)  and  H(Y)≤H(XY) ,  therefore also  H(X|Y)≤H(XY)  and  H(Y|X)≤H(XY)  hold.  Thus, a conditional entropy can never become larger than the joint entropy.


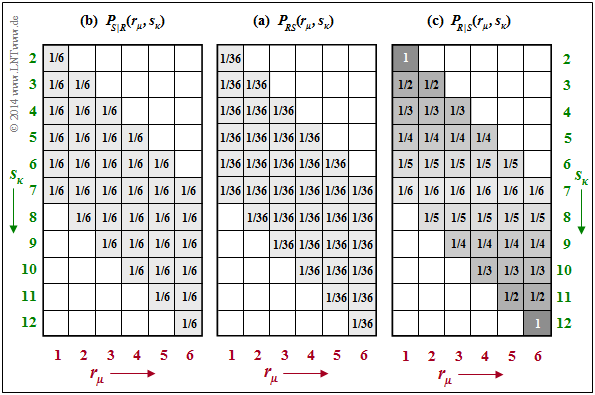
Example 2:  We consider the joint probabilities  PRS(·)  of our dice experiment, which were determined in the  "last chapter"  as  Example 6.  The corresponding  PRS(·)  is given again in the middle of the following graph.

Joint probabilities  PRS  and conditional probabilities  PS|R  and  PR|S

The two conditional probability functions are drawn on the outside:

On the left  you see the conditional probability mass function 

PS|R(⋅)=PSR(⋅)/PR(⋅).
  • Because of  PR(R)=[1/6, 1/6, 1/6, 1/6, 1/6, 1/6]  the probability  1/6  is in all shaded fields  
  • That means:   supp(PS|R)=supp(PR|S)  . 
  • From this follows for the conditional entropy:
H(S∣R)=∑(r,s)∈supp(PRS)PRS(r,s)⋅log21PS∣R(s∣r)
⇒H(S∣R)=36⋅136⋅log2(6)=2.585 bit.

On the right,  PR|S(⋅)=PRS(⋅)/PS(⋅)  is given with  PS(⋅)  according to  Example 6. 

  • supp(PR|S)=supp(PS|R)   ⇒  same non-zero fields result.
  • However, the probability values now increase continuously from the centre  (1/6)  towards the edges up to  1  in the corners.
  • It follows that:
H(R∣S)=136⋅log2(6)+236⋅5∑i=1[i⋅log2(i)]=1.896 bit.

On the other hand, for the conditional probabilities of the 2D random variable  RB  according to  Example 5,  one obtains because of  PRB(⋅)=PR(⋅)·PB(⋅):

H(B∣R)=H(B)=log2(6)=2.585 bit,H(R∣B)=H(R)=log2(6)=2.585 bit.


Mutual information between two random variables


We consider the two-dimensional random variable  XY  with PMF  PXY(X,Y). Let the one-dimensional functions  PX(X)  and  PY(Y) also be known.

Now the following questions arise:

  • How does the knowledge of the random variable  Y  reduce the uncertainty with respect to  X?
  • How does the knowledge of the random variable  X  reduce the uncertainty with respect to  Y?


To answer this question, we need a definition that is substantial for information theory:

Definition:  The  »mutual information« between the random variables  X  and  Y – both over the same alphabet – is given as follows:

I(X; Y)=E[log2PXY(X,Y)PX(X)⋅PY(Y)]=∑(x,y)∈supp(PXY)PXY(x,y)⋅log2PXY(x,y)PX(x)⋅PY(y).

A comparison with the  "last chapter"  shows that the mutual information can also be written as a  Kullback–Leibler distance  between the two-dimensional probability mass function  PXY  and the product  PX·PY  :

I(X;Y)=D(PXY||PX⋅PY).

It is thus obvious that  I(X; Y)≥0  always holds.  Because of the symmetry,   I(Y; X) = I(X; Y) is also true.


By splitting the  log2 argument according to

I(X;Y)=E[log21PX(X)]−E[log2PY(Y)PXY(X,Y)]

is obtained using  PX|Y(⋅)=PXY(⋅)/PY(Y):

I(X;Y)=H(X)−H(X∣Y).
  • This means:   The uncertainty regarding the random quantity  X   ⇒   entropy  H(X)  decreases by the magnitude  H(X|Y)  when  Y is known.  The remainder is the mutual information  I(X;Y).
  • With a different splitting, one arrives at the result
I(X;Y)=H(Y)−H(Y∣X).
  • Ergo:   The mutual information  I(X;Y)  is symmetrical   ⇒   X  says just as much about  Y  as  Y  says about  X   ⇒   "mutual".  The semicolon indicates equality.


Conclusion:  Often the equations mentioned here are clarified by a diagram, as in the following examples. 
From this you can see that the following equations also apply:

I(X; Y)=H(X)+H(Y)−H(XY),
I(X; Y)=H(XY)−H(X∣Y)−H(Y∣X).


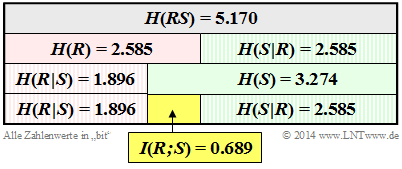
Example 3:  We return  (for the last time)  to the  dice experiment  with the red  (R)  and blue  (B)  cube.  The random variable  S  gives the sum of the two dice:  S=R+B.  Here we consider the 2D random variable  RS. 

In earlier examples we calculated

  • the entropies  H(R)=2.585 bit  and  H(S)=3.274 bit   ⇒  Example 6  in the last chapter,
  • the join entropies  H(RS)=5.170 bit   ⇒   Example 6  in the last chapter,
  • the conditional entropies  H(S|R)=2.585 bit  and  H(R|S)=1.896 bit   ⇒   Example 2  in the previous section.
Diagram of all entropies of the "dice experiment"


These quantities are compiled in the graph, with the random quantity  R  marked by the basic colour "red" and the sum  S  marked by the basic colour "green" .  Conditional entropies are shaded.  One can see from this representation:

  • The entropy  H(R)=log2(6)=2.585 bit  is exactly half as large as the joint entropy  H(RS).  Because:  If one knows  R,  then  S  provides exactly the same information as the random quantity  B, namely  H(S|R)=H(B)=log2(6)=2.585 bit. 
  • Note:   H(R) = H(S|R)  only applies in this example, not in general.
  • As expected, here the entropy  H(S)=3.274 bit  is greater than  H(R)=2.585 bit.  Because of  H(S)+H(R|S)=H(R)+H(S|R) ,  H(R|S)  must therefore be smaller than  H(S|R)  by   I(R; S)=0.689 bit .   H(R)  is also smaller than  H(S) by   I(R; S)=0.689 bit .
  • The mutual information between the random variables  R  and  S  also results from the equation
I(R; S)=H(R)+H(S)−H(RS)=2.585 bit+3.274 bit−5.170 bit=0.689 bit.


Conditional mutual information


We now consider three random variables  X,  Y  and  Z, that can be related to each other.

Definition:  The   »conditional mutual information«   between the random variables  X  and  Y  for a given  Z=z  is as follows:

I(X;Y|Z=z)=H(X|Z=z)−H(X|Y,Z=z).

One denotes as the conditional  »conditional mutual information«  between the random variables  X  and  Y  for the random variable  Z  in general 
after averaging over all  z∈Z:

I(X;Y|Z)=H(X|Z)−H(X|YZ)=∑z∈supp(PZ)PZ(z)⋅I(X;Y|Z=z).

PZ(Z)  is the probability mass function  (PMF)  of the random variable  Z  and  PZ(z)  is the  »probability«  for the realization  Z=z.


Please note: 

  • For the conditional entropy, as is well known, the relation   H(X|Z)≤H(X)  holds.
  • For the mutual information, this relation does not necessarily hold:
        I(X;Y|Z)  can be  smaller, equal, but also larger than  I(X;Y).


2D PMF  PXZ

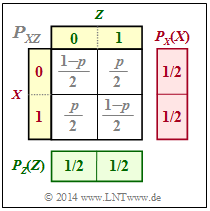
Example 4:  We consider the binary random variables  X,  Y  and  Z  with the following properties:

  • X  and  Y  be statistically independent.  Let the following be true for their probability mass functions:
PX(X)=[1/2, 1/2],PY(Y)=[1–p, p] ⇒ H(X)=1 bit,H(Y)=Hbin(p).
  • Z  is the modulo-2 sum of  X  and  Y:   Z=X⊕Y.


From the joint probability mass function  PXZ  according to the upper graph, it follows:

  • Summing the column probabilities gives 
        PZ(Z)=[1/2, 1/2]   ⇒   H(Z)=1 bit.
  • X  and  Z  are also statistically independent, since for the 2D PMF holds 
        PXZ(X,Z)=PX(X)·PZ(Z) . 
Conditional 2D PMF PX|YZ
  • It follows that:
        H(Z|X)=H(Z),(X|Z)=H(X),I(X;Z)=0.


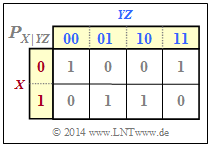
From the conditional probability mass function  PX|YZ  according to the graph below, we can calculate:

  • H(X|YZ)=0,  since all  PX|YZ entries are  0  or  1   ⇒   "conditional entropy",
  • I(X;YZ)=H(X)−H(X|YZ)=H(X)=1 bit   ⇒   "mutual information",
  • I(X;Y|Z)=H(X|Z)=H(X)=1 bit   ⇒   "conditional mutual information".


In the present example:

The conditional mutual information  I(X;Y|Z)=1  is greater than the conventional mutual information  I(X;Y)=0.


Chain rule of the mutual information


So far we have only considered the mutual information between two one-dimensional random variables.  Now we extend the definition to a total of  n+1  random variables, which, only for reasons of representation, we denote with  X1,  ... ,  Xn  and  Z  .  Then applies:

Chain rule of mutual information: 

The mutual information between the  n–dimensional random variable  X1X2...Xn  and the random variable  Z  can be represented and calculated as follows:

I(X1X2...Xn;Z)=I(X1;Z)+I(X2;Z|X1)+...+I(Xn;Z|X1X2...Xn−1)=n∑i=1I(Xi;Z|X1X2...Xi−1).

Proof:  We restrict ourselves here to the case  n=2, i.e. to a total of three random variables, and replace  X1  by X and  X2  by  Y.  Then we obtain:

I(XY;Z)=H(XY)−H(XY|Z)==[H(X)+H(Y|X)]−[H(X|Z)+H(Y|XZ)]==[H(X)−H(X|Z)]−[H(Y|X)+H(Y|XZ)]==I(X;Z)+I(Y;Z|X).


  • From this equation one can see that the relation  I(XY;Z)≥I(X;Z)  is always given.
  • Equality results for the conditional mutual information  I(Y;Z|X)=0,  i.e. when the random variables  Y  and  Z  for a given  X  are statistically independent.


Example 5:  We consider the  Markov chain   X→Y→Z.  For such a constellation, the  "Data Processing Theorem"  always holds with the following consequence, which can be derived from the chain rule of mutual information:

I(X;Z)≤I(X;Y),
I(X;Z)≤I(Y;Z).

The theorem thus states:

  • One cannot gain any additional information about the input  X  by manipulating the data  Y  by processing   Y→Z.
  • Data processing  Y→Z  (by a second processor) only serves the purpose of making the information about  X  more visible.


For more information on the  "Data Processing Theorem"  see  "Exercise 3.15".


Exercises for the chapter


Exercise 3.7: Some Entropy Calculations

Exercise 3.8: Once more Mutual Information

Exercise 3.8Z: Tuples from Ternary Random Variables

Exercise 3.9: Conditional Mutual Information




Retrieved from "http://en.lntwww.de/index.php?title=Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables&oldid=52782"
  • Powered by MediaWiki