Exercise 5.8: Equalization in Matrix Vector Notation

• Return to book

Blockschaltbild der OFDM-Übertragung

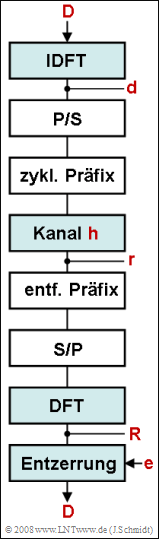
Wir betrachten die in der Grafik hinterlegten Blöcke eines OFDM–Systems, wobei wir von einem System mit $N = 4$ Trägern und einem Kanal mit $L = 2$ Echos ausgehen.

• Es wird nur ein einziger Rahmen betrachtet und für den Sendevektor (im Zeitbereich) gelte:

$${\rm\bf{d}} = (d_0, d_1,d_2,d_3 ) = (+1, -1, +1, -1 ).$$

• Die Kanalimpulsantwort sei beschrieben durch

$${\rm\bf{h}} = (h_0, h_1,h_2 ) = (0, 0.6, 0.4 ).$$

• Zur Repräsentation des zyklischen Präfixes verwenden wir in dieser Aufgabe statt des erweiterten Sendevektors mit der zugehörigen Übertragungsmatrix $H_{ext}$ die zyklische Übertragungsmatrix

$${\rm\bf{H}}_{\rm{C}} = \left( {\begin{array}{*{20}c} {h_0 } & {h_1 } & {h_2 } & {} \\ {} & {h_0 } & {h_1 } & {h_2 } \\ \hline {h_2 } & {} & {h_0 } & {h_1 } \\ {h_1 } & {h_2 } & {} & {h_0 } \\ \end{array}} \right).$$

• Für die Spektralkoeffizienten am Empfänger gelte nach der Diskreten Fouriertransformation (DFT):

$${\rm\bf{R}} = {\rm\bf{D}} \cdot \left( {\begin{array}{*{20}c} {H_0 } & {} & {} & {} \\ {} & {H_1 } & {} & {} \\ {} & {} & {H_2 } & {} \\ {} & {} & {} & {H_3 } \\ \end{array}} \right) ,$$

wobei die Diagonalelemente wie folgt zu berechnen sind:

$$H_\mu = \sum\limits_{l = 0}^2 {h_l \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi }} \hspace{0.04cm}\cdot \hspace{0.04cm} l \hspace{0.04cm}\cdot \hspace{0.04cm} {\mu }/{4}} } .$$

• Die Entzerrung am Empfänger erfolgt durch Multiplikation im Frequenzbereich mit den Koeffizienten $e_\mu = {1}/{H_\mu }.$

Hinweise:

• Die Aufgabe gehört zum Kapitel Realisierung von OFDM-Systemen.
• Bezug genommen wird auch auf das Kapitel Diskrete Fouriertransformation im Buch „Signaldarstellung”.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Für die Diskrete Fouriertransformation (DFT) gilt in Matrix–Vektor–Notation:

$${\rm\bf{F}} = \left( {\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ 1 & {} & {} & {} \\ \vdots & {} & {{\rm{e}}^{ - {\rm{j2\pi }}{\kern 1pt} \nu {\kern 1pt} \mu /N} } & {} \\ 1 & {} & {} & {} \\ \end{array}} \right), \qquad {\rm{DFT\; mit}} \; {1}/{N} \cdot {\rm\bf{F}}; \qquad {\rm{IDFT \; mit}} \; {\rm\bf{F}}^*.$$

Fragebogen

1

Berechnen Sie die diskreten Empfangswerte $r = (r_0, r_1, r_2, r_3)$ im Zeitbereich. Geben Sie zur Kontrolle $r_0$ und $r_1$ ein:

${\rm Re}[r_0] \ = \ $

${\rm Im}[r_0] \ = \ $

${\rm Re}[r_1] \ = \ $

${\rm Im}[r_0] \ = \ $

2

Wie lauten die diskreten Spektralbereichskoeffizienten ${\rm\bf{D}}= (D_0, D_1, D_2, D_3)$ am Sender? Geben Sie zur Kontrolle $D_2$ und $D_3$ ein.

${\rm Re}[D_2] \ = \ $

${\rm Im}[D_2] \ = \ $

${\rm Re}[D_3] \ = \ $

${\rm Im}[D_3] \ = \ $

3

Berechnen Sie die diskreten Spektralkoeffizienten ${\rm\bf{R}}= (R_0, R_1, R_2, R_3)$ nach dem Kanal. Geben Sie zur Kontrolle $R_2$ und $R_3$ ein:

${\rm Re}[R_2] \ = \ $

{\rm Im}[R_2] \ = \ $

{\rm Re}[R_3] \ = \ $

{\rm Im}[R_2] \ = \ $

4

Bestimmen Sie die diskreten Entzerrerkoeffizienten ${\rm\bf{e}}= (e_0, e_1, e_2, e_3)$:

${\rm Re}[e_0] \ = \ $

${\rm Im}[e_0] \ = \ $

${\rm Re}[e_1] \ = \ $

${\rm Im}[e_1] \ = \ $

${\rm Re}[e_2] \ = \ $

${\rm Im}[e_2] \ = \ $

${\rm Re}[e_3] \ = \ $ {-0.78--0.76 }

${\rm Im}[e_3] \ = \ $

5

Wie bezeichnet man den verwendeten Entzerrungsansatz?

	Als „Zero Forcing”–Ansatz,
	als „Matched Filter”–Ansatz,
	als „Minimum Mean Square Error (MMSE)”–Ansatz.

Musterlösung

Solution

1. Die diskreten Zeitbereichswerte am Empfänger berechnen sich mit der zyklischen Übertragungsmatrix $H_C$ wie folgt: $${\rm\bf{r}} = {\rm\bf{d}} \cdot {\rm\bf{H_C}} = \left( {+1 ,-1 ,+1 ,-1 } \right) \cdot \left( {\begin{array}{*{20}c} {0 } & {0.6 } & {0.4 } & {} \\ {} & {0 } & {0.6 } & {0.4 } \\ \hline {0.4 } & {} & {0 } & {0.6 } \\ {0.6 } & {0.4 } & {} & {0 } \\ \end{array}} \right)$$ $$\Rightarrow \hspace{0.3cm}{\rm\bf{r}} = \left( {r_0 ,r_1 ,r_2 ,r_3 } \right) = \left( {-0.2, +0.2,-0.2, +0.2} \right) .$$ Damit sind alle Empfangswerte r₀ = –0.2, r₁ = +0.2, r₂ = –0.2 und r₃ = +0.2 rein reell.

2. Die Spektralkoeffizienten D ergeben sich direkt aus der Diskreten Fouriertransformation (DFT) der Zeitbereichskoeffizienten d = (+1, –1, +1, –1). Diese Zeitbereichsfolge entspricht einer diskreten Cosinusfunktion mit der doppelten Grundfrequnz (2 · f₀) und der Amplitude 1. Daraus folgt: $${\rm\bf{D}} = \left( {D_0 ,D_1 ,D_2 ,D_3 } \right) \hspace{0.15cm} \underline{=\left( {0, 0,1, 0} \right)} .$$

3. Der Vektor R der Spektralkoeffizienten nach dem Kanal könnte analog zur Teilaufgabe b) durch die DFT des Vektors r berechnet werden. Ein alternativer Lösungsweg lautet: $${\rm\bf{R}} = {\rm\bf{D}} \cdot \left( {\begin{array}{*{20}c} {H_0 } & {} & {} & {} \\ {} & {H_1 } & {} & {} \\ {} & {} & {H_2 } & {} \\ {} & {} & {} & {H_3 } \\ \end{array}} \right) .$$ Für die Diagonalelemente erhält man: $$H_\mu = \sum\limits_{l = 0}^2 {h_l \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi }} \hspace{0.04cm}\cdot \hspace{0.04cm} l \hspace{0.04cm}\cdot \hspace{0.04cm}{\mu }/{4}} }$$ $$\Rightarrow \hspace{0.3cm} H_0 = 1,\hspace{0.1cm}H_1 = -0.4 - {\rm{j}} \cdot 0.6,\hspace{0.1cm}H_2 = -0.2,\hspace{0.1cm}H_3 = -0.4 + {\rm{j}} \cdot 0.6$$ $$\Rightarrow \hspace{0.3cm}{\rm\bf{R}} = \left( {R_0 ,R_1 ,R_2 ,R_3 } \right) \hspace{0.15cm} \underline{= \left( {\hspace{0.15cm}0,\hspace{0.15cm}0,-0.2, \hspace{0.15cm}0} \right)} .$$

4. Die Entzerrerkoeffizienten ergeben sich zu e_μ = 1/H_μ. Mit dem Ergebnis zu Teilaufgabe c) sind die Koeffizienten e₀ = 1 und e₂ = –5 reell, während für μ = 1, μ = 3 gilt: $$e_1 = \frac {1}{-0.4 - {\rm{j}} \cdot 0.6}$$ $$\Rightarrow \hspace{0.3cm} {\rm{Re}}[e_1] = \frac {-0.4}{0.4^2 + 0.6^2}\hspace{0.15cm} \underline{ \approx -0.77},\hspace{0.3cm} {\rm{Im}}[e_1] = \frac {0.6}{0.4^2 + 0.6^2} \hspace{0.15cm} \underline{\approx 1.15},$$ $$e_3 = \frac {1}{-0.4 + {\rm{j}} \cdot 0.6}$$ $$\Rightarrow \hspace{0.3cm} {\rm{Re}}[e_3] = \frac {-0.4}{0.4^2 + 0.6^2}\hspace{0.15cm} \underline{ \approx -0.77},\hspace{0.3cm} {\rm{Im}}[e_3] = \frac {-0.6}{0.4^2 + 0.6^2} \hspace{0.15cm} \underline{\approx -1.15}.$$ 5. Die unter d) berechnete Entzerrung folgt dem „Zero Forcing”–Ansatz.