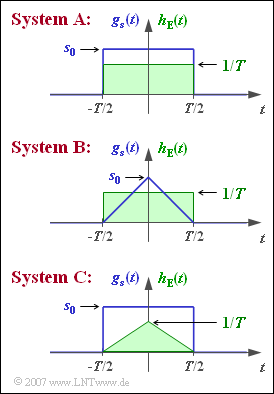
Exercise 1.3: Rectangular Functions for Transmitter and Receiver

• Return to book

Vergleich dreier verschiedener Systemkonzepte

Wir betrachten hier drei Varianten eines binären bipolaren AWGN–Übertragungssystems, die sich hinsichtlich des Sendegrundimpulses $g_{s}(t)$ sowie der Impulsantwort $h_{\rm E}(t)$ des Empfangsfilters unterscheiden:

• Beim System A sind sowohl $g_{s}(t)$ als auch $h_{\rm E}(t)$ rechteckförmig, lediglich die Impulshöhen ($s_{\rm 0}$ bzw. $1/T$) sind unterschiedlich.
• Das System B unterscheidet sich vom System A durch einen dreieckförmigen Sendegrundimpuls mit $g_{s}(t=0) = s_{\rm 0}$.
• Das System C hat den gleichen Sendegrundimpuls wie System A, während die Impulsantwort mit $h_{\rm E}(t=0) = 1/T$ dreieckförmig verläuft.

Die absolute Breite der hier betrachteten Rechteck– und Dreieckfunktionen beträgt jeweils $T = 10 \ \rm \mu s$. Die Bitrate ist $R = 100 \ \rm kbit/s$. Die weiteren Systemparameter sind wie folgt gegeben:

$$s_0 = 6 \,\,\sqrt{W}\hspace{0.05cm},\hspace{0.3cm} N_{\rm 0} = 2 \cdot 10^{-5} \,\,{\rm W/Hz}\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Fehlerwahrscheinlichkeit bei Basisbandübertragung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Zur Bestimmung von Fehlerwahrscheinlichkeiten können Sie das Interaktionsmodul Komplementäre Gaußsche Fehlerfunktionen verwenden.
• Berücksichtigen Sie bei der Berechnung der Detektionsstörleistung das Theorem von Wiener–Chintchine:

$$\sigma _d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H_{\rm E}( f )} \right|^2 \hspace{0.1cm}{\rm{d}}f} = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {h_{\rm E}( t )} \right|^2 \hspace{0.1cm}{\rm{d}}t}\hspace{0.05cm}.$$

Fragebogen

1

Berechnen Sie für System A den Detektionsgrundimpuls $g_{d}(t) = g_{ s}(t) \star h_{\rm E}(t)$ . Welcher Wert $g_0 = g_{d}(t=0)$ ergibt sich zum Zeitpunkt $t = 0$?

$g_0 \hspace{0.28cm} = \ $ $\ \rm W^{1/2}$

2

Berechnen Sie daraus die Detektionsstörleistung $σ_{\rm d}^2$.

$σ_{d}^{\hspace{0.02cm}2} \hspace{0.2cm} = \ $ $\ \rm W$

3

Welche Bitfehlerwahrscheinlichkeit $p_{\rm B}$ ergibt sich somit für das System A?

$p_{\rm B} \hspace{0.2cm} = \ $ $\ \cdot 10^{-9}$

4

Ermitteln Sie die entsprechenden Größen für System B.

$g_0 \hspace{0.28cm} = \ $ $\ \rm W^{1/2}$

$σ_{d}^{\hspace{0.02cm}2} \hspace{0.2cm} = \ $ $\ \rm W$

$p_{\rm B} \hspace{0.2cm} = \ $ $\ \cdot 10^{-2}$

5

Wie lauten die Kenngrößen für das System C?

$g_0 \hspace{0.28cm} = \ $ $\ \rm W^{1/2}$

$σ_{d}^{\hspace{0.02cm}2} \hspace{0.2cm} = \ $ $\ \rm W$

$p_{\rm B} \hspace{0.2cm} = \ $ $\ \cdot 10^{-7}$

Musterlösung

Solution

1.  Beim System A führt die Faltung der beiden gleich breiten Rechteckfunktionen $g_{s}(t)$ und $h_{\rm E}(t)$ zu einem dreieckförmigen Detektionsgrundimpuls mit dem Maximum bei $t = 0$:

$$g_d (t = 0) = \int_{ - T/2}^{ + T/2} { g_s(t) \cdot h_{\rm E}( t )} \hspace{0.1cm}{\rm{d}}t =s_0 \cdot \frac{1 }{T} \cdot T = s_0 \hspace{0.1cm}\underline { = 6 \,\,\sqrt{{\rm W}}}\hspace{0.05cm}.$$

Es gibt keine Impulsinterferenzen, da für $| t |\ge T$ der Detektionsimpuls $g_{d}(t) = 0$ ist.

2.  Die Varianz des Detektionsstörsignals – hier als Detektionsstörleistung bezeichnet – kann sowohl im Zeit– als auch im Frequenzbereich berechnet werden. Bei der vorliegenden Rechteckform führt die Berechnung im Zeitbereich schneller zum Ergebnis:

$$\sigma _d ^2 \ = \ \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {h_{\rm E}( t )} \right|^2 \hspace{0.1cm}{\rm{d}}t} =\frac{N_0 }{2} \cdot \int_{ - T/2 }^{ + T/2 } {\left| {h_{\rm E}( t )} \right|^2 \hspace{0.1cm}{\rm{d}}t} = \ \frac{N_0 }{2} \cdot\frac{1 }{T^2} \cdot T = \frac{N_0 }{2T} = \frac{2 \cdot 10^{-5} \,\,{\rm W/Hz}}{2 \cdot 10^{-5} \,\,{\rm s}} \hspace{0.1cm}\underline {= 1\,{\rm W}}\hspace{0.05cm}.$$

Die Frequenzbereichsberechnung würde mit $H_{\rm E}(f) = {\rm si}(πfT)$ wie folgt aussehen:

$$\sigma _d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H_{\rm E}( f )} \right|^2 \hspace{0.1cm}{\rm{d}}f} = \frac{N_0 }{2} \cdot \int_{- \infty }^{ \infty } {\rm si}^2(\pi f T)\hspace{0.1cm}{\rm{d}}f = \frac{N_0 }{2T} \hspace{0.05cm}.$$

3.  Aufgrund der zeitlich begrenzten Impulsform (das bedeutet: keine Impulsinterferenzen!) ergibt sich bei der hier vorausgesetzten bipolaren Betrachtungsweise:

$$p_{\rm B} = {\rm Q} \left( \frac{s_0}{\sigma_d}\right)= {\rm Q} \left( \frac{ 6 \,\sqrt{\rm W}}{1 \,\sqrt{\rm W}}\right) = {\rm Q}(6) \hspace{0.1cm}\underline {= 0.987 \cdot 10^{-9}} \hspace{0.05cm}.$$

System A stellt die Matched–Filter–Realisierung des optimalen Binärempfängers dar, so dass auch folgende Gleichungen anwendbar wären:

$$E_{\rm B} = s_0^2 \cdot T = 36\, {\rm W} \cdot 10^{-5} {\rm s}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B} = {\rm Q} \left( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0}}\right) ={\rm Q} \left( \sqrt{\frac{2 \cdot 36 \cdot 10^{-5}\,\, {\rm Ws}}{2 \cdot 10^{-5} \,\, {\rm Ws}}}\right)={\rm Q}(6) \hspace{0.05cm}.$$

4.  Da bei System B das gleiche Empfangsfilter wie bei System A verwendet wird, erhält man auch die gleiche Detektionsstörleistung $σ_{d}^2 = 1 \ \rm W$. Der Detektionsgrundimpuls ist nun aber nicht mehr dreieckförmig, sondern weist eine spitzere Form auf. Zum Zeitpunkt $t = 0$ gilt:

$$g_d (t = 0) = \frac{1}{T} \cdot \int_{ - T/2}^{ + T/2} { g_s(t) } \hspace{0.1cm}{\rm{d}}t = \frac{1}{T} \cdot \frac{s_0 }{2} \cdot T = \frac{s_0 }{2}\hspace{0.1cm}\underline {= 3 \,\,\sqrt{\rm W}}\hspace{0.05cm}.$$

Auch das System B ist impulsinterferenzfrei. Man erhält deshalb für die Bitfehlerwahrscheinlichkeit:

$$p_{\rm B} = {\rm Q} \left( \frac{g_d (t = 0)}{\sigma_d}\right)= {\rm Q} \left( \frac{ 3 \,\sqrt{\rm W}}{1 \,\sqrt{\rm W}}\right) = {\rm Q}(3) \hspace{0.1cm}\underline {= 0.135 \cdot 10^{-2}} \hspace{0.05cm}.$$

Nicht anwendbar ist dagegen hier der folgende Rechengang:

$$E_{\rm B} = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t = 2\cdot s_0^2 \cdot \int ^{+T/2} _{0} \left( 1- \frac{2t}{T}\right)^2\,{\rm d}t = \frac{s_0^2 \cdot T }{3} = 12 \cdot 10^{-5} \,{\rm Ws}$$

$$\Rightarrow \hspace{0.3cm} p_{\rm B} = {\rm Q} \left( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0}}\right) ={\rm Q} \left( \sqrt{12}\right)={\rm Q}(3.464) \approx 3 \cdot 10^{-4} \hspace{0.05cm}.$$

Man würde so eine zu niedrige Bitfehlerwahrscheinlichkeit berechnen, da die implizit getroffene Annahme eines angepassten Filters nicht zutrifft.

5.  Bei rechteckförmigem Sendegrundimpuls und dreieckförmiger Impulsantwort   ⇒   System C erhält man den gleichen Detektionsgrundimpuls wie bei dreieckförmigem $g_{\rm s}(t)$ und rechteckförmigem $h_{\rm E}(t)$. Wie beim System B gilt deshalb:

$$g_d (t = 0) = \frac{s_0}{2}\hspace{0.1cm}\underline {= 3 \,\,\sqrt{\rm W}}\hspace{0.05cm}.$$

Dagegen ist nun die Detektionsstörleistung kleiner als bei den Systemen A und B:

$$\sigma _d ^2 = \frac{N_0}{2} \cdot \frac{1}{T^2} \cdot \int^{+T/2} _{-T/2} \left( 1- \frac{2t}{T}\right)^2\,{\rm d}t = \frac{N_0}{6T}\hspace{0.1cm}\underline { = 0.333 \,{\rm W}}.$$

Damit erhält man nun für die Bitfehlerwahrscheinlichkeit:

$$p_{\rm B} = {\rm Q} \left( \frac{ 3 \,\sqrt{\rm W}}{0.577 \,\sqrt{\rm W}}\right) \approx {\rm Q}(5.2)\hspace{0.1cm}\underline { \approx 10^{-7} } \hspace{0.05cm}.$$

Der gegenüber Teilfrage (3) erkennbare Anstieg der Fehlerwahrscheinlichkeit um etwa den Faktor $100$ ist auf die gravierende Fehlanpassung gegenüber dem Matched–Filter zurückzuführen. Die Verbesserung gegenüber Teilaufgabe (4) geht auf die höhere Signalenergie zurück.