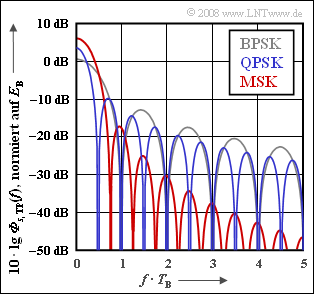
Exercise 4.15: MSK Compared with BPSK and QPSK

Leistungsdichtespektren: BPSK, QPSK, MSK

Verglichen werden die Leistungsdichtespektren (im äquivalenten Tiefpassbereich) von

Binary Phase Shift Keying (BPSK),
Quaternary Phase Shift Keying (QPSK),
Minimum Shift Keying (MSK).

Diese sind in der Grafik logarithmisch dargestellt, wobei die Frequenz auf den Kehrwert der Bitdauer $T_{\rm B}$ normiert ist.

Für die BPSK und die QPSK ist jeweils ein rechteckförmiger Grundimpuls der Höhe $s_0$ und der Symboldauer $T$ vorausgesetzt. Damit gilt für die BPSK und die QPSK (bzw. die 4–QAM und die Offset–QPSK) gleichermaßen:

${\it \Phi}_{s}(f) = \frac{s_0^2 \cdot T}{4} \cdot \big [ {\rm si}^2 ( \pi T \cdot (f- f_{\rm T}) ) + {\rm si}^2 ( \pi T \cdot (f+ f_{\rm T}) ) \big ]\hspace{0.05cm},$

und in den äquivalenten Tiefpassbereich transformiert:

${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 ( \pi f T ) \hspace{0.05cm}.$

Trotz gleicher Formel weisen die BPSK und die QPSK unterschiedliche Leistungsdichtespektren auf:

Bei der BPSK (graue Kurve) ist die Symboldauer $T$ gleich der Bitdauer $T_{\rm B}$ und es gilt mit der Energie pro Bit $(E_{\rm B} = s_0^2 · T_{\rm B}/2)$ :

${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = E_{\rm B} \cdot {\rm si}^2 ( \pi f T_{\rm B} ) \hspace{0.05cm}.$

Dagegen ist bei der QPSK (blaue Kurve) bei gleichem $E_{\rm B}$ die Symboldauer $T$ doppelt so groß:

${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = 2 \cdot E_{\rm B} \cdot {\rm si}^2 ( 2\pi f T_{\rm B} ) \hspace{0.05cm}.$

Bei der Berechnung des MSK–Spektrums (rote Kurve) kann berücksichtigt werden, dass die MSK als Offset–QPSK entsprechend dem Blockschaltbild im Theorieteil realisiert werden kann, wenn der folgende Grundimpuls verwendet wird:

$g(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$

In der Aufgabe 4.14Z wird die zugehörige Spektralfunktion berechnet:

$G(f) = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$

Berücksichtigen Sie weiterhin:

Die beiden Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ sind trotz der Vorcodierung unkorreliert.
Bei MSK ist entgegen der QPSK wie bei der BPSK $T = T_{\rm B}$ zu setzen.
Auch bei MSK ist die Energie pro Bit wie folgt gegeben: $E_{\rm B} = s_0^2 · T/2$ .
Der Betrag des Tiefpass–Signals $|s_{\rm TP}(t)| = s_0$ ist gleich dem Maximalwert $g_0$ des Grundimpulses $g(t)$ .

Hinweise:

Die Aufgabe gehört zum Kapitel Nichtlineare digitale Modulation.
Bezug genommen wird insbesondere auf den Abschnitt Realisierung der MSK als Offset-QPSK.

Das Leistungsdichtespektrums im äquivalenten Tiefpassbereich eines Zweiges – zum Beispiel: Inphasekomponente – lautet:

${\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = \frac{1}{2 T} \cdot {\rm E} \left [ a_\nu ^2 \right ] \cdot |G(f)|^2 \hspace{0.05cm}.$

Fragebogen

$f_1 \ = \$

$\ \cdot 1/T_{\rm B}$

$f_1 \ = \$

$\ \cdot 1/T_{\rm B}$

${\itΦ}_\text{s, TP}(f = 0) \ = \$

$\ \cdot E_{\rm B}$

	Die erste LDS–Nullstelle kommt bei MSK früher als bei QPSK.
	Das MSK–Leistungsdichtespektrum klingt schneller ab.
	Bei MSK ist das Integral über ${\itΦ}_\text{s, TP}(f)$ (nicht logarithmiert) größer als bei QPSK.

Musterlösung

Solution

(1) Aus der angegebenen Gleichung und der Grafik erkennt man, dass bei Binary Phase Shift Keying (BPSK) die erste Nullstelle des Leistungsdichtespektrums bei

$f_1\hspace{0.15cm}\underline{ =1} \cdot 1/T_{\rm B}$ liegt.

(2) Aufgrund der niedrigeren Symbolrate $1/T$ ist bei Quaternary Phase Shift Keying (QPSK) – und bei allen verwandten quaternären Modulationsverfahren – das Spektrum nur halb so breit wie bei der BPSK ⇒ $f_1\hspace{0.15cm}\underline{ =0.5} \cdot 1/T_{\rm B}$ .

(3) Für das Leistungsdichtespektren (LDS) des Gesamtsignals gilt im äquivalenten Tiefpassbereich:

${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) + {\it \Phi}_{s,\hspace{0.05cm} {\rm Q},\hspace{0.05cm} {\rm TP}}(f)= 2 \cdot {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = {1}/{ T} \cdot |G(f)|^2\hspace{0.05cm}.$

Hierbei ist berücksichtigt, dass

die Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ unkorreliert sind, so dass man die LDS–Anteile addieren kann,
wegen der binären bipolaren Amplitudenkoeffizienten der Erwartungswert $E[a_ν^2] = 1$ ist.

Damit erhält man:

${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{1}{ T} \cdot \left ( \frac {4}{\pi} \right ) ^2 \cdot g_0^2 \cdot T^2 \cdot \frac{ {\rm cos}^2 ( 2 \pi f T )}{ \big [1 - (4 f T)^2 \big ] ^2} \hspace{0.05cm}.$

Mit $s_0 = g_0$ , $T = T_{\rm B}$ und $E_{\rm B} = s_0^2 · T_{\rm B}/2$ gilt weiter:

${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{32}{ \pi^2} \cdot E_{\rm B} \cdot \frac{ {\rm cos}^2 ( 2 \pi \cdot f \cdot T_{\rm B} )}{ \big [1 - (4 \cdot f \cdot T_{\rm B})^2 \big ] ^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f = 0 )= \frac{32}{ \pi^2} \cdot E_{\rm B} \hspace{0.15cm}\underline {\approx 3.243 \cdot E_{\rm B}} \hspace{0.05cm}.$

(4) Richtig ist nur der Lösungsvorschlag 1:

Bereits aus der Grafik ist zu ersehen, dass die erste Aussage falsch und die zweite richtig ist.
Der Lösungsvorschlag 3 stimmt ebenfalls nicht. Das Integral über die Leistungsdichtespektren ergibt die Leistung $(E_{\rm B}/T_{\rm B})$ .
Die Signalverläufe von BPSK, QPSK und MSK machen deutlich, dass die Leistung bei konstanter Hüllkurve $(s_0)$ für alle betrachteten Modulationsverfahren gleich ist.