Exercise 5.4: Walsh Functions (PCCF, PACF)

• Return to book

Hadamard–Matrix  ${\mathbf{H}_{8}}$

Häufig verwendet man zur Bandspreizung und Bandstauchung so genannte  Walsh–Funktionen, die mittels der Hadamard–Matrix konstruiert werden können. Ausgehend von der Matrix

$${\mathbf{H}_{2}} = \left[ \begin{array}{ccc} +1 & +1 \\ +1 & -1 \end{array} \right]$$

lassen sich durch folgende Rekursion die weiteren Hadamard–Matrizen  ${\mathbf{H}_{4}}$,  ${\mathbf{H}_{8}}$, usw. herleiten:

$${\mathbf{H}_{2J}} = \left[ \begin{array}{ccc} \mathbf{H}_J & \mathbf{H}_J \\ \mathbf{H}_J & -\mathbf{H}_J \end{array} \right] \hspace{0.05cm}.$$

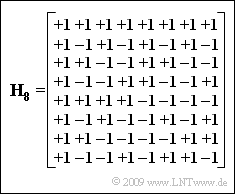
Die Grafik zeigt die Matrix  ${\mathbf{H}_{8}}$  für den Spreizfaktor  $J = 8$. Daraus lassen sich die Spreizfolgen

$$\langle w_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle w_\nu^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$...$$

$$\langle w_\nu^{(7)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$

für sieben CDMA–Teilnehmer ablesen. Die Spreizfolge  $\langle w_\nu^{(0)}\rangle$  entsprechend der ersten Zeile in der Hadamard–Matrix wird meistens nicht vergeben, da sie nicht spreizt.

Die Fragen beziehen sich meist auf den Spreizfaktor  $J = 4$. Damit können entsprechend mit den Spreizfolgen  $\langle w_\nu^{(1)}\rangle$,  $\langle w_\nu^{(2)}\rangle$  und  $\langle w_\nu^{(3)}\rangle$  maximal drei CDMA–Teilnehmer versorgt werden, die sich aus der zweiten, dritten und vierten Zeile der Matrix ${\mathbf{H}_{4}}$ ergeben.

Hinsichtlich der Korrelationsfunktionen soll in dieser Aufgabe folgende Nomenklatur gelten:

• Die  periodische Kreuzkorrelationsfunktion  (PKKF) zwischen den Folgen  $\langle w_\nu^{(i)}\rangle$  und  $\langle w_\nu^{(j)}\rangle$  wird mit  $φ_{ij}(λ)$  bezeichnet. Hierbei gilt:

$${\it \varphi}_{ij}(\lambda) = {\rm E}\left [ w_{\nu}^{(i)} \cdot w_{\nu+ \lambda}^{(j)} \right ] \hspace{0.05cm}.$$

• Ist die PKKF  $φ_{ij} \equiv 0$  (das heißt:  $φ_{ij}(λ) = 0$  für alle Werte von  $λ$), so stören sich die CDMA–Teilnehmer nicht, auch wenn zwei Teilnehmer unterschiedliche Laufzeiten aufweisen.
• Gilt zumindest  $φ_{ij}({\it λ} = 0) = 0$, so kommt es zumindest bei synchronem CDMA–Betrieb (keine oder gleiche Laufzeiten aller Teilnehmer) zu keinen Interferenzen.
• Die  periodische Autokorrelationsfunktion  (PAKF) der Walsh–Funktion  $\langle w_\nu^{(i)}\rangle$  wird mit  $φ_{ii}(λ)$  bezeichnet, und es gilt:

$${\it \varphi}_{ii}(\lambda) = {\rm E}\left [ w_{\nu}^{(i)} \cdot w_{\nu+ \lambda}^{(i)} \right ] \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Spreizfolgen für CDMA.
• Bezug genommen wird insbesondere auf den Abschnitt  Walsh–Funktionen  im Theorieteil.
• Wir möchten Sie gerne auch auf das Interaktionsmodul Walsh-Funktionen hinweisen.

• Die Abszisse ist auf die Chipdauer  $T_c$  normiert. Das bedeutet, dass  $λ = 1$  eigentlich eine Verschiebung um die Verzögerungszeit  $τ = T_c$  beschreibt.

Fragebogen

1

Wie lauten die Spreizfolgen für  $J = 4$?

	$\langle w_\nu^{(1)}\rangle = +\hspace{-0.05cm}1 -\hspace{-0.15cm}1 +\hspace{-0.15cm}1 -\hspace{-0.15cm}1$,
	$\langle w_\nu^{(2)}\rangle = +\hspace{-0.05cm}1 +\hspace{-0.15cm}1 -\hspace{-0.15cm}1 -\hspace{-0.15cm}1$,
	$\langle w_\nu^{(3)}\rangle = +\hspace{-0.05cm}1 -\hspace{-0.15cm}1 -\hspace{-0.15cm}1 +\hspace{-0.15cm}1$.

2

Welche Aussagen gelten bezüglich der PKKF–Werte  $φ_{ij}(λ = 0)$?

	Für $J = 4$  ist  $φ_{12}(λ = 0) = 0$.
	Für $J = 4$  ist  $φ_{13}(λ = 0) = 0$.
	Für $J = 4$  ist  $φ_{23}(λ = 0) = 0$.
	Für $J = 8$  kann durchaus  $φ_{ij}(λ = 0) ≠ 0$  gelten  $(i ≠ j)$.
	Bei synchronem CDMA stören sich die Teilnehmer nicht.

3

Welche Aussagen gelten für die PKKF–Werte mit  $λ ≠ 0$?

	Für alle Werte von  $λ$  ist die PKKF  $φ_{12}(λ) = 0$.
	Für alle Werte von  $λ$  ist die PKKF  $φ_{13}(λ) = 0$.
	Für alle Werte von  $λ$  ist die PKKF  $φ_{23}(λ) = 0$.
	Bei asynchronem CDMA stören sich die Teilnehmer nicht.

4

Welche Aussagen gelten für die PAKF–Kurven?

	Alle  $φ_{ii}(λ)$–Kurven sind periodisch.
	Es gilt  $φ_{11}(λ = 0) = +\hspace{-0.05cm}1$  und  $φ_{11}(λ = 1) = -\hspace{-0.05cm}1$.
	Es gilt  $φ_{22}(λ) = φ_{11}(λ)$.
	Es gilt  $φ_{33}(λ) = φ_{22}(λ)$.

Musterlösung

Solution

(1)  Alle Vorschläge sind richtig:

• Die Matrix ${\mathbf{H}_{4}}$ ist die linke obere Teilmatrix von ${\mathbf{H}_{8}}$.
• Die Spreizfolgen ergeben sich aus den Zeilen 2, 3 und 4 von ${\mathbf{H}_{4}}$, und stimmen mit den angegebenen Folgen überein.

(2)  Richtig sind die Lösungsvorschläge 1, 2 und 3:

• Entsprechend den Gleichungen im Angabenteil gilt:

$${\it \varphi}_{12}(\lambda = 0) = 1/4 \cdot \left [ (+1) \cdot (+1) + (-1) \cdot (+1) + (+1) \cdot (-1) + (-1) \cdot (-1) \right ] = 0\hspace{0.05cm},$$

$${\it \varphi}_{13}(\lambda = 0) = 1/4\cdot \left [ (+1) \cdot (+1) + (-1) \cdot (-1) + (+1) \cdot (-1) + (-1) \cdot (+1) \right ] = 0\hspace{0.05cm},$$

$${\it \varphi}_{23}(\lambda = 0) =1/4 \cdot \left [ (+1) \cdot (+1) + (+1) \cdot (-1) + (-1) \cdot (-1) + (-1) \cdot (+1) \right ] = 0\hspace{0.05cm}.$$

• Auch für größere Werte von $J$ ist für $i ≠ j$ der PKKF–Wert stets $φ_{ij}(λ = 0)= 0$.
• Daraus folgt: Bei synchronem CDMA stören sich die Teilnehmer nicht.

(3)  Richtig sind die Lösungsvorschläge 1 und 2:

• Für alle Werte von $λ$ ist dieie PKKF $φ_{12}(λ) = 0$, wie die folgenden Zeilen zeigen:

$$\langle w_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$ $$\langle w_\nu^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle w_{\nu+1}^{(2)}\rangle = {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle w_{\nu+2}^{(2)}\rangle = {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle w_{\nu+3}^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle w_{\nu+4}^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} = \langle w_\nu^{(2)}\rangle \hspace{0.05cm}.$$

• Das gleiche gilt für die PKKF $φ_{13}(λ)$.
• Dagegen erhält man für die PKKF zwischen den Folgen $\langle w_\nu^{(2)}\rangle$ und $\langle w_\nu^{(3)}\rangle$:

Verschiedene PKKF– und PAKF–Kurven

$${\it \varphi}_{23}(\lambda ) = \left\{ \begin{array}{c}0 \\+1\\ -1 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c} \lambda = 0, \pm 2, \pm 4,\pm 6, ... \hspace{0.05cm}, \\ \hspace{0.14cm} \lambda = ... \hspace{0.05cm} , -3, +1, +5, ... \hspace{0.05cm}, \\ \hspace{0.14cm} \lambda = ... \hspace{0.05cm} , -5, -1, +3, ... \hspace{0.05cm}. \\ \end{array}$$

• Das bedeutet: Wird das Signal von Teilnehmer 3 gegenüber Teilnehmer 2 um ein Spreizchip verzögert oder umgekehrt, so lassen sich die Teilnehmer nicht mehr trennen und es kommt zu einer signifikanten Erhöhung der Fehlerwahrscheinlichkeit.
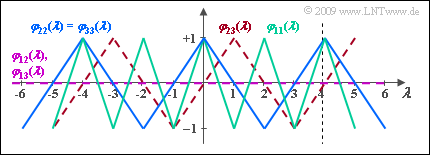
• In der Grafik sind die PKKF–Kurven gestrichelt eingezeichnet (violett und rot).

(4)  Richtig sind die Aussagen 1, 2 und 4:

• Da die Walsh–Funktion Nr. 1 periodisch ist mit $T_0 = 2T_c$, ist auch die PAKF periodisch mit $λ = 2$.
• Die zweite Aussage ist richtig, wie die folgende Rechnung zeigt (grüner Kurvenzug):

$${\it \varphi}_{11}(\lambda = 0) = 1/4 \cdot \left [ (+1) \cdot (+1) + (-1) \cdot (-1) + (+1) \cdot (+1) + (-1) \cdot (-1) \right ] = +1\hspace{0.05cm},$$

$${\it \varphi}_{11}(\lambda = 1) = 1/4 \cdot \left [ (+1) \cdot (-1) + (+1) \cdot (-1) + (+1) \cdot (-1) + (+1) \cdot (-1) \right ] = -1\hspace{0.05cm}.$$

• Da sich die beiden Walsh–Funktionen Nr. 2 und 3 nur durch eine Verschiebung um $T_c$ unterscheiden und sich eine Phase in der PAKF prinzipiell nicht auswirkt, ist tatsächlich entsprechend dem letzten Lösungsvorschlag $φ_{33}(λ) = φ_{22}(λ)$. Diese beiden PAKF–Funktionen sind blau eingezeichnet.
• Dagegen unterscheidet sich $φ_{22}(λ)$ von $φ_{11}(λ)$ durch eine andere Periodizität: $φ_{22}(λ) = φ_{33}(λ)$ ist doppelt so breit wie $φ_{11}(λ)$.