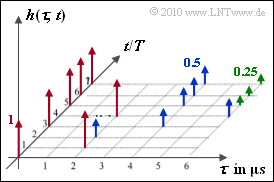
Exercise 2.1: Two-Dimensional Impulse Response

• Return to book

Two-dimensional impulse response

The two-dimensional impulse response

$$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)$$

is to be analyzed according to the adjoining diagram.  The two axes are discrete-time:

• $\tau$  is the  delay  and can take values between  $0$  and  $6 \ {\rm µ s}$  in the example.
• The (absolute) time  $t$  is related to the frequency of snapshots and characterizes the variation of the channel over time. We have  $t = n \cdot T$, where  $T \gg \tau_{\rm max}$ .

The arrows in the graphic mark different Dirac functions with weights  $1$  (red),  $1/2$  (blue) and  $1/4$  (green). This means that the delay  $\tau$  is also discrete here.

When measuring the impulse responses at different times  $t$  at intervals of one second, the resolution of the  $\tau$–axis was two microseconds $(\delta \tau = 2 \ \rm µ s)$.  The echoes were not localized more precisely.

In this task the following quantities are also referred to:

• the "time-variant transfer function"  according to the definition

$$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm},$$

• the approximation of the "coherence bandwidth"  as the reciprocal of the maximal duration of the delay profile  $h(\tau, t)$:

$$B_{\rm K} \hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$

Notes:

• This task belongs to the chapter  General description of time–variant systems.
• More detailed information on various definitions for the coherence bandwidth can be found in chapter  The GWSSUS channel model, especially in the sample solution for the  Exercise 2.7Z.
• It should be noted that this is a constructed task.  According to the above graph, the 2D impulse response changes significantly during the time span  $T$.  Therefore  $T$  is to be interpreted here as very large, for example one hour.
• In mobile radio,  $h(\tau, t)$  changes in the millisecond range taking into account the Doppler effect, but the changes during this time are rather moderate.

Questionnaire

1

What restriction does the specification  $\Delta \tau = 2 \rm µ s$  impose on the maximum bandwidth  $B_{\rm max}$  of the signal to be examined?

$B_{\rm max} \ = \ $ $\ \ \rm kHz$

2

At what time  $t_2$  the channel is ideal, characterized by  $H(f, t_{\rm 2}) = 1$?

$t_{\rm 2} \ = \ $ $\ \cdot T$

3

From what time  $t_{\rm 3}$  this channel does cause distortion?

$t_{\rm 3} \ = \ $ $\ \cdot T$

4

Calculate the coherence bandwidth for  $t = 3T$,  $t = 4T$  and  $t = 5T$:

$t = 3T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ $ $\ \ \rm kHz$

$t = 4T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ $ $\ \ \rm kHz$

$t = 5T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ $ $\ \ \rm kHz$

5

From what time  $t_{\rm 5}$  this channel could be considered as time–invariant?

$t_{\rm 5} \ = \ $ $\ \cdot T$

6

For which of the mentioned  values of  $T$  does it make sense to work with the  $\rm 2D$–impulse response?

	A (slow) channel change occurs approximately after  $T = 1 \ \rm µ s$.
	A (slow) channel change takes place approximately after  $T = 1 \ \rm s$.

Solution

Solution

(1)  The signal described in the equivalent low-pass range should not have a bandwidth greater than  $B_{\rm max} = 1/\Delta \tau \ \underline {= 500 \ \rm kHz}$.

• This mathematical (two-sided) bandwidth of the low-pass signal is also the maximum physical (one-sided) bandwidth of the corresponding band-pass signal.

(2)  $H(f, t_{\rm 2}) = 1$  means in the time domain  $h(\tau, t_{\rm 2}) = \delta(\tau)$.

• Only then the channel is ideal.
• You can see from the graph that this only applies to the time  $t_{\rm 2} \ \underline {= 0}$.

(3)  Distortions occur if at time  $t$  the impulse response is composed of two or more Dirac functions   ⇒   $t ≥ t_{\rm 3} \ \underline {= 3T}$.

• At time  $t = T$  the signal  $s(t)$  is delayed only by  $2 \ \rm µ s$.
• At  $t = 2T$  the amplitude is additionally reduced by  $50 \%$  $(6 \ \ \rm dB$ loss$)$.

(4)  At time  $t = 3T$  the two Dirac functions occur at  $\tau_{\rm min} = 0$  and  $\tau_{\rm max} = 4 \ \rm µ s$.

• The (simple approximation for the) coherence bandwidth is the reciprocal of the delay span of these Dirac functions:

$$B_{\rm K}\hspace{0.01cm}' = \frac{1}{4\,\,{\rm µ s} } \hspace{0.25cm} \underline{ = 250\,\,{\rm kHz}} \hspace{0.05cm}.$$

• The same as at  $t = 4T$  the time between the Dirac functions is  $4 \ \rm µ s$:  $B_{\rm K} \hspace{0.01cm}' = \underline {250 \ \rm kHz}$.
• At  $t = 5T$  the impulse response has a duration of  $6 \ \ \rm µ s \ \ \Rightarrow \ {\it B}_{\rm K} \hspace{0.01cm}' \ \underline {\approx 166.7 \ \rm kHz}$.

(5)  The impulse responses are identical at the times  $5T$,  $6T$  and  $7T$  each consists of three Diracs.

• Assuming that nothing changes in this respect for  $t ≥ 8T$:   $t_{\rm 5} \ \ \underline {= 5T}$.

(6)  Solution 2 is correct:

• The temporal change of the impulse response, whose dynamics is expressed by the parameter  $T$, must be slow in comparison to the maximum delay span of  $h(\tau, t)$, which is in this task equals $\tau_{\rm max} = 6 \ \rm µ s$   ⇒   $T \gg \tau_{\rm max}.$