Exercise 4.6: k-parameters and alpha-parameters

• Return to book

Attenuation function per unit length,
valid for  "copper twin wire"  (0.5 mm)

For symmetrical copper twisted pairs,  the following empirical formula can be found in  [PW95],  which is valid for the frequency range  $0 \le f \le 30 \ \rm MHz$:

$$\alpha_{\rm I} (f) = k_1 + k_2 \cdot (f/f_0)^{k_3} , \hspace{0.15cm} f_0 = 1\,{\rm MHz} .$$

In contrast,  the attenuation function per unit length of a coaxial cable is usually given in the following form:

$$\alpha_{\rm II}(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}\hspace{0.05cm}.$$

Especially for the calculation of impulse response and rectangular response it is advantageous also for the copper twisted pairs to choose the second representation form with the cable parameters  $\alpha_0$,  $\alpha_1$  and  $\alpha_2$  instead of the representation with  $k_1$,  $k_2$  and  $k_3$.

For the conversion,  one proceeds as follows:

• From above equations,  it is obvious that the coefficient characterizing the DC signal attenuation is  $\alpha_0 = k_1$.
• To determine  $\alpha_1$  and  $\alpha_2$,  it is assumed that the mean square error should be minimum in the range of a given bandwidth  $B$:

$${\rm E}\big[\varepsilon^2(f)\big] = \int_{0}^{ B} \left [ \alpha_{\rm II} (f) - \alpha_{\rm I} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$

• The difference  $\varepsilon^2(f)$  and the mean square error  ${\rm E}\big[\varepsilon^2(f)\big]$  are obtained as follows:

$$\varepsilon^2(f) = \big [ \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f} - k_2 \cdot (f/f_0)^{k_3}\big ]^2 =\alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm} f^2 + 2 \alpha_1 \alpha_2 \hspace{0.05cm}\cdot\hspace{0.05cm} f^{1.5} + \alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm} f + k_2^2\hspace{0.05cm}\cdot\hspace{0.05cm} \frac{f^{2k_3}}{f_0^{2k_3}} - 2 k_2 \alpha_1 \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{f^{k_3+1}} {f_0^{k_3}}-{2 k_2 \alpha_2} \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{f^{k_3+0.5}}{f_0^{k_3}}$$

$$\Rightarrow \hspace{0.3cm}{\rm E}\big[\varepsilon^2(f)\big] = \alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm}\frac{B^3}{3} + \frac{4}{5} \hspace{0.05cm}\cdot\hspace{0.05cm}\alpha_1 \alpha_2 \hspace{0.05cm}\cdot\hspace{0.05cm}B^{2.5} + \alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{B^2}{2} + \frac{k_2^2}{2k_3 +1} \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{B^{2k_3+1}}{f_0^{2k_3}} - \hspace{0.15cm} \frac{2 k_2 \alpha_1}{k_3 + 2} \hspace{0.05cm}\cdot\hspace{0.05cm}$$

This equation contains the cable parameters  $\alpha_1$,  $\alpha_2$,  $k_2$  and  $k_3$  to be calculated as well as the bandwidth  $B$,  within which the approximation should be valid.

• By setting the derivatives of  ${\rm E}\big[\varepsilon^2(f)\big]$  to  $\alpha_1$  and  $\alpha_2$  to zero, two equations are obtained for the best possible coefficients  $\alpha_1$  and  $\alpha_2$ that minimize the mean square error. These can be represented in the following form:

$$\frac{{\rm d}\,{\rm E}\big[\varepsilon^2(f)\big]}{{\rm d}\,{\alpha_1}} = 0 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \alpha_1 + C_1 \cdot \alpha_2 + C_2 = 0 \hspace{0.05cm} ,$$

$$\frac{{\rm d}\,{\rm E}\big[\varepsilon^2(f)\big]}{{\rm d}\,{\alpha_2}} = 0 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \alpha_1 + D_1 \cdot \alpha_2 + D_2 = 0 \hspace{0.05cm} .$$

• From the equation  $C_1 \cdot \alpha_2 + C_2 = D_1 \cdot \alpha_2 + D_2$,  the coefficient  $\alpha_2$  can be calculated and then the coefficient  $\alpha_1$ can be calculated from each of the two equations above.

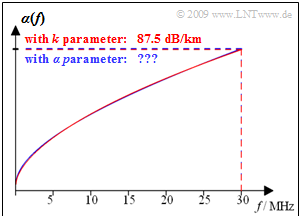
The graph shows the attenuation function per unit length for a copper twin wire with  $\text{0.5 mm}$  diameter, whose  $k$–parameters are:

$$k_1 = 4.4\, {\rm dB}/{\rm km} \hspace{0.05cm}, \hspace{0.2cm} k_2 = 10.8\, {\rm dB}/{\rm km}\hspace{0.05cm}, \hspace{0.2cm}k_3 = 0.60\hspace{0.05cm} \hspace{0.05cm}.$$

• The red curve shows the function  $\alpha(f)$  calculated with this parameters.  For  $f = 30 \ \rm MHz$  the attenuation function per unit length is  $\alpha(f)= 87.5 \ \rm dB/km$.
• The blue curve gives the approximation with the  $\alpha$–coefficients.  This is almost indistinguishable from the red curve within the drawing accuracy.

Notes:

• The exercise belongs to the chapter  Properties of Balanced Copper Pairs.

• You can use the  (German language)  interactive SWF applet  "Dämpfung von Kupferkabeln"  ⇒   "Attenuation of copper cables" .
• [PW95]  denotes the following literature reference:   Pollakowski, P.; Wellhausen, H.-W.:  Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz.  Deutsche Telekom AG, Forschungs- und Technologiezentrum Darmstadt, 1995.

Questions

1

Calculate the parameters  $C_1$  and  $C_2$  of the equation  $\alpha_1 + C_1 \cdot \alpha_2 + C_2 = 0$  resulting from the derivative  ${\rm dE\big[\text{...}\big]/d}\alpha_1$. 
Which results are correct?

	$C_1 = 6/5 \cdot B^{-0.5}$,
	$C_1 = 5/4 \cdot B^{-0.5}$,
	$C_1 = 4/3 \cdot B^{2}$,
	$C_2 = -4/3 \cdot B^{-2$}$,
	$C_2 = -5/2 \cdot k_2/(k_3 +1.5) \cdot B^{k_3 -1} \cdot f_0^{-k_3}$,
	$C_2 = -3 \cdot k_2/(k_3 +2) \cdot B^{k_3 -1} \cdot f_0^{-k_3}$.

2

Calculate the parameters  $D_1$  and  $D_2$  of the equation  $\alpha_1 + D_1 \cdot \alpha_2 + D_2 = 0$  resulting from the derivative  ${\rm dE\big[\text{...}\big]/d}\alpha_2$. 
Which results are correct?

	$D_1 = 6/5 \cdot B^{-0.5}$,
	$D_1 = 5/4 \cdot B^{-0.5}$,
	$D_1 = 4/3 \cdot B^{2}$,
	$D_2 = -4/3 \cdot B^{-2}$,
	$D_2 = -5/2 \cdot k_2/(k_3 +1.5) \cdot B^{k_3 -1} \cdot f_0^{-k_3}$,
	$D_2 = -3 \cdot k_2/(k_3 +2) \cdot B^{k_3 -1} \cdot f_0^{-k_3}$.

3

Calculate the coefficients  $\alpha_1$  and  $\alpha_2$  for the given  $k_2$  and  $k_3$.
Which of the following statements are true?

	For  $k_3=1.0$,   $\alpha_1 = k_2/f_0$  and  $\alpha_2 = 0$.
	For  $k_3=0.5$,   $\alpha_1 = 0$  and  $\alpha_2 = k_2/f_0^{0.5}$.

4

Determine the coefficients  $\alpha_1$  and  $\alpha_2$  numerically for the approximation bandwidth  $B = 30 \ \rm MHz$.

$\alpha_1 \ = \ $ $\ \rm dB/(km\ \cdot \ MHz)$

$\alpha_2 \ =\ $ $\ \rm dB/(km\ \cdot \ \sqrt{\rm MHz})$

5

Using the  $\alpha$–parameters,  calculate the attenuation function per unit length for the frequency  $f = 30\ \rm MHz$.

$\alpha_{\rm II}(f = 30\ \rm MHz) \ = \ $ $\ \rm dB/km$

Solution

Solution

(1)  Solutions 1 and 6  are correct:

• The derivative of the given expected value with respect to  $\alpha_1$  gives:

$$\frac{{\rm d}\,{\rm E}[\varepsilon^2(f)]}{{\rm d}\,{\alpha_1}} = \frac{2}{3}\cdot B^3 \cdot \alpha_1 + \frac{4}{5}\cdot B^{2.5} \cdot \alpha_2 - \frac{2 k_2 }{k_3 + 2} \cdot \frac{B^{k_3+2}}{f_0^{k_3}}= 0 \hspace{0.05cm} .$$

• By setting it to zero and dividing by  $2B^2/3$,  we obtain:

$$\alpha_1 + \frac{6}{5}\cdot B^{-0.5} \cdot \alpha_2 - \frac{3 k_2 }{k_3 +2} \cdot \frac{B^{k_3-1}}{f_0^{k_3}}= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} C_1 = \frac{6}{5}\cdot B^{-0.5} \hspace{0.05cm} , \hspace{0.5cm} C_2 = - \frac{3 k_2 }{k_3 +2} \cdot \frac{B^{k_3-1}}{f_0^{k_3}} \hspace{0.05cm} .$$

(2)  Solutions 2 and 5  are correct:

• Using the same procedure as in subtask  (1),  we obtain:

$$\frac{{\rm d}\,{\rm E}[\varepsilon^2(f)]}{{\rm d}\,{\alpha_2}} = \frac{4}{5}\cdot B^{2.5} \cdot \alpha_1 + B^{2} \cdot \alpha_2 - \frac{2 k_2 }{k_3 + 1.5} \cdot \frac{B^{k_3+1.5}}{f_0^{k_3}}= 0$$

$$\Rightarrow \hspace{0.3cm} \alpha_1 + \frac{5}{4}\cdot B^{-0.5} \cdot \alpha_2 - \frac{2.5 \cdot k_2 }{k_3 +1.5} \cdot \frac{B^{k_3-1}}{f_0^{k_3}}= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_1 = \frac{5}{4}\cdot B^{-0.5} \hspace{0.05cm} , \hspace{0.3cm}D_2 = - \frac{2.5 \cdot k_2 }{k_3 +1.5} \cdot \frac{B^{k_3-1}}{f_0^{k_3}} \hspace{0.05cm} .$$

(3)  Both solutions  are correct:

• From  $C_1 \cdot \alpha_2 + C_2 = D_1 \cdot \alpha_2 + D_2$  we obtain a linear equation for  $\alpha_2$.  With the result from  (2)  we can write:

$$\alpha_2 = \frac{D_2 - C_2}{C_1 - D_1} = \frac{- \frac{2.5 \cdot k_2 }{k_3 +1.5} \cdot \frac{B^{k_3-1}}{f_0^{k_3}} + \frac{3 k_2 }{k_3 +2} \cdot \frac{B^{k_3-1}}{f_0^{k_3}}}{{6}/{5}\cdot B^{-0.5} - {5}/{4}\cdot B^{-0.5}} = \frac{- {2.5 \cdot k_2 }\cdot(k_3 +2) + {3 k_2 }\cdot (k_3 +1.5) }{({6}/{5} - {5}/{4})(k_3 +1.5)(k_3 +2)} \cdot \frac{B^{k_3-0.5}}{f_0^{k_3}}$$

$$\Rightarrow \hspace{0.3cm}\alpha_2 = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0}} \hspace{0.05cm} .$$

• For the parameter   $\alpha_1$  then holds:

$$\alpha_1 = - C_1 \cdot \alpha_2 - C_2 = -\frac{6}{5}\cdot B^{-0.5} \cdot 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0}} +\frac{3 k_2 }{k_3 +2} \cdot \frac{B^{k_3-1}}{f_0^{k_3}}$$

$$\Rightarrow \hspace{0.3cm}\alpha_1 = (B/f_0)^{k_3 -1}\cdot \frac{-12 \cdot (1-k_3) + 3 \cdot (k_3 + 1.5)}{(k_3 + 1.5)(k_3 + 2)} \cdot \frac {k_2}{f_0} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\alpha_1 =15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{f_0}\hspace{0.05cm} .$$

• Regardless of the bandwidth,  we obtain for  $k_3 = 1$:

$$\alpha_1 = (B/f_0)^{k_3 -1}\cdot \frac{15 \cdot (k_3 -0.5)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{f_0} = \frac{15 \cdot 0.5}{2.5 \cdot 3}\cdot \frac {k_2}{f_0} \hspace{0.15cm}\underline{ = {k_2}/{f_0}}\hspace{0.05cm} ,$$

$$\alpha_2 = (B/f_0)^{k_3 -0.5}\cdot \frac{10 \cdot (1-k_3)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0}}\hspace{0.15cm}\underline{= 0} \hspace{0.05cm} .$$

• In contrast,  for  $k_3 = 0.5$:

$$\alpha_1 = (B/f_0)^{k_3 -1}\cdot \frac{15 \cdot (k_3 -0.5)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{f_0} \hspace{0.15cm}\underline{= 0}\hspace{0.05cm} ,$$

$$\alpha_2 = (B/f_0)^{k_3 -0.5}\cdot \frac{10 \cdot (1-k_3)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0}}= \frac{10 \cdot 0.5}{2 \cdot 2.5}\cdot \frac {k_2}{\sqrt{f_0}} = \hspace{0.15cm}\underline{ {k_2}/{\sqrt{f_0}}} \hspace{0.05cm} .$$

(4)  For the two coefficients, with  $k_2 = 10.8 \ \rm dB/km$,  $k_3 = 0.6 \ \rm dB/km$  and  $B/f_0 = 30$:

$$\alpha_1 = (B/f_0)^{k_3 -1}\cdot \frac{15 \cdot (k_3 -0.5)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{f_0} = 30^{-0.4}\cdot \frac{15 \cdot 0.1}{2.1 \cdot 2.6}\cdot \frac {10.8 \, {\rm dB/km} }{1 \, {\rm MHz}} \hspace{0.15cm}\underline{ \approx 0.761\, {{\rm dB} }/{({\rm km \cdot MHz})}} \hspace{0.05cm} ,$$

$$\alpha_2 = (B/f_0)^{k_3 -0.5}\cdot \frac{10 \cdot (1-k_3)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0}}= \frac {k_2}{\sqrt{f_0}} = 30^{0.1}\cdot \frac{10 \cdot 0.4}{2.1 \cdot 2.6}\cdot \frac {10.8 \, {\rm dB/km} }{1 \, {\rm MHz^{0.5}}} \hspace{0.15cm}\underline{ \approx 11.1\, {{\rm dB} }/{({\rm km \cdot \sqrt{MHz}}})}\hspace{0.05cm} .$$

(5)  According to the given equation  $\alpha_{\rm II}(f)$  thus also holds:

$$\alpha_{\rm II}(f = 30 \, {\rm MHz}) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f} = \big [ \hspace{0.05cm} 4.4 + 0.761 \cdot 30 + 11.1 \cdot \sqrt {30}\hspace{0.05cm} \big ]\frac {\rm dB}{\rm km } \hspace{0.15cm}\underline{\approx 88.1\, {\rm dB}/{\rm km }} \hspace{0.05cm}.$$