Exercise 3.1Z: Triangular PDF

• Return to book

Triangular PDF and
characteristic curve  $y(x)$

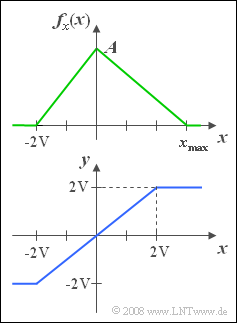
We consider a continuous random variable  $x$  with the PDF outlined on the right. 

• The minimum value of the signal is  $x_{\rm min} = -2\hspace{0.05cm} {\rm V}$. 
• On the other hand,  the maximum value  $x_{\rm max}$  is a free parameter,  allowing values between  $+2\hspace{0.05cm}\rm V$  and  $+4\hspace{0.05cm} \rm V$.

The random variable  $x$  is to be understood here as the instantaneous value of a random signal.  If this signal  $x(t)$  is applied to an amplitude limiter with the characteristic curve  (see sketch below)

$$y(t)=\left\{\begin{array}{*{4}{c}} -2\hspace{0.05cm} {\rm V} & {\rm if}\hspace{0.1cm} x(t)<-2\hspace{0.05cm} {\rm V} , \\ x(t) & {\rm if}\hspace{0.1cm}-2\hspace{0.05cm} {\rm V} \le x(t)\le +2\hspace{0.05cm} {\rm V}, \\ +2\hspace{0.05cm} {\rm V} & {\rm if}\hspace{0.1cm} {\it x}({\it t})>+2\hspace{0.05cm} {\rm V}, \\\end{array}\right.$$

so the signal  $y(t)$  or the new random variable  $y$,  which is considered in the last two subquestions  (5)  and  (6)  is obtained.

• For the subtasks  (1)  and  (2)  apply  $x_{\rm max} = 2\hspace{0.05cm} {\rm V}$.
• For all other subtasks,  set  $x_{\rm max} = 4\hspace{0.05cm} {\rm V}$ .

Hints:

• The task belongs to the chapter  Probability Density Function.

• The topic of this chapter is illustrated with examples in the  (German language)  learning video 
     "Wahrscheinlichkeit und WDF"   $\Rightarrow$   "Probability and PDF".

Questions

1

Let be  $x_{\rm max} = +2\hspace{0.05cm} {\rm V}$.  Calculate the parameter  $A = f_x(0)$.

$A \ = \ $ $\ \rm 1/V$.

2

Let  $x_{\rm max} = +2\hspace{0.05cm} {\rm V}$.  What is the probability that  $|x(t)|$  less than  $x_{\rm max}/2$?

${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}| < 1\hspace{0.05cm} {\rm V}) \ = \ $

3

Now let be  $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$.  What is the probability that  $x$  lies between  $+1\hspace{0.05cm} {\rm V}$  and  $+3\hspace{0.05cm} {\rm V}$?

${\rm Pr}(1\hspace{0.05cm} {\rm V} < x <3\hspace{0.05cm} {\rm V}) \ = \ $

4

Let further be  $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$.  What is the probability that  $x$  is exactly equal to $+2\hspace{0.05cm} {\rm V}$?

${\rm Pr}(x =2\hspace{0.05cm} {\rm V})\ = \ $

5

Let further be  $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$.  Which of the following statements is true?

	$y$  is a continuous random variable.
	$y$  is a discrete random variable.
	$y$  is a mixed continuous-discrete random variable.

6

Let further be  $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$.  What is the probability that  $y$  is exactly equal  $+2\hspace{0.05cm} {\rm V}$?

${\rm Pr}(y =2\hspace{0.05cm} {\rm V})\ = \ $

Solution

Solution

Height and area of triangular PDF

(1)  The area under the PDF must always yield the value  $1$.  It follows that:

$${A}/{ 2}\cdot {4\hspace{0.05cm}\rm V}=1\hspace{0.5cm}\Rightarrow\hspace{0.5cm} A \hspace{0.15cm}\underline{=\rm 0.5\;{1}/{V}}.$$

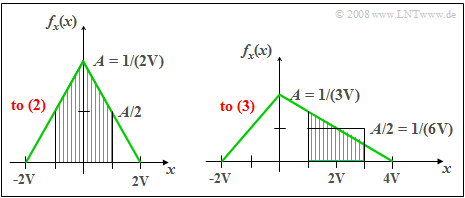
(2)  With  $x_{\rm max} = +2\hspace{0.05cm} {\rm V}$  the PDF is obtained according to the left graph.

• The shading marks the probability we are looking for.
• One obtains by simple geometric considerations:

$${\rm Pr}(|x|<\rm 1\hspace{0.05cm} V)\hspace{0.15cm}\underline{=\rm 0.75}.$$

(3)  With  $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$  one obtains the PDF shown on the right.

• The maximum value is now   $A = 1/(3\hspace{0.05cm} {\rm V})$.
• The shaded area again indicates the probability we are looking for,  which can be determined using the rectangle of equal area:

$${\rm Pr}(1\hspace{0.05cm} {\rm V}< x<3\hspace{0.05cm} {\rm V})=\rm \frac{1}{6\hspace{0.05cm} {\rm V}}\cdot 2\hspace{0.05cm} {\rm V}=\hspace{0.15cm}\underline{0.333}.$$

(4)  Since  $x$  represents a continuous random variable,  this probability is by definition zero   ⇒   ${\rm Pr}(x =2\hspace{0.05cm} {\rm V}) \;\underline {= 0}$.

Mixed continuous/discrete PDF

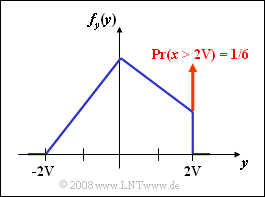
(5)  Only the last statement of the given answers is true:

• The PDF  $f_y(y)$  includes a continuous component (drawn in blue),
• but also the (red) Dirac delta function at  $y = +2\hspace{0.05cm} {\rm V}$  with weight  ${\rm Pr}(x >2\hspace{0.05cm} {\rm V})$.

(6)  The graphic on the right shows the probability density function of the random variable  $y$.

• From the right figure for subtask  (3)  one can see the relation:

$${\rm Pr}( y=2\hspace{0.05cm} {\rm V}) = {\rm Pr}( x> 2\hspace{0.05cm} {\rm V}) = \frac{1}{2}\cdot\frac{1}{6\hspace{0.05cm} {\rm V}}\cdot2{\hspace{0.05cm} {\rm V}} = {1}/{6}\hspace{0.15cm}\underline{=0.167}.$$