Exercise 4.13Z: AMI Code

• Return to book

Auto-correlation functions at the input and output of AMI coding

For spectral adaptation  (shaping)  of a digital signal to the characteristics of the channel,  one uses so-called  "pseudo-ternary codes".  With these codes,  the binary source symbol sequence  $\langle q_\nu \rangle$  is converted to a sequence  $\langle c_\nu \rangle$  of ternary symbols according to a fixed rule:

$$q_{\nu} \in \{ -1,\hspace{0.1cm} +1 \} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_{\nu} \in \{ -1, \hspace{0.1cm}0, \hspace{0.1cm}+1 \} .$$

The best known representative of this code class is the AMI code  (from  "Alternate Mark Inversion").  Here

• the binary value  $q_\nu = -1$  is always mapped to  $c_\nu = 0$ ,
• while  $q_\nu = +1$  is alternately represented by the ternary values  $c_\nu = +1$  and  $c_\nu = -1$.

By convention,  the ternary symbol  $c_\nu = +1$  shall be selected at the first occurrence of  $q_\nu = +1$ .

It is further assumed that

• the two possible source symbols are each equally probable and
• the source symbol sequence  $\langle q_\nu \rangle$ has no internal statistical bindings.

Thus,  all discrete ACF values are zero except  $\varphi_q(k=0)$:

$$\varphi_q ( k \cdot T) = 0 \hspace{0.5cm} {\rm if} \hspace{0.5cm} k \not= 0.$$

Here  $T$  denotes the time distance between the source symbols. Use  $T = 1 \hspace{0.05cm} \rm µ s$. The code symbols have the same spacing.

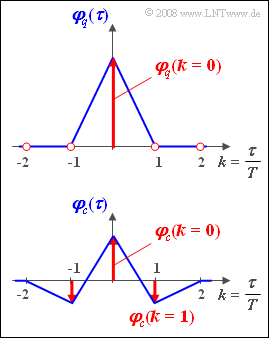
The graphic shows the given auto-correlation functions.  Please note:

• In red are respectively the discrete-time representations  ${\rm A} \{ \varphi_q(\tau) \}$  and  ${\rm A} \{ \varphi_c(\tau) \}$  of the auto-correlation functions,  each with the reference value  $T$.
• The functions shown in blue indicate the continuous-time progressions  $\varphi_q(\tau)$  and  $\varphi_c(\tau)$  of the ACF,  assuming square-wave pulses.

Hints:

• This exercise belongs to the chapter  Power-Spectral Density.
• Reference is also made to the chapter  Auto-Correlation Function  as well as to the page  Numerical PSD determination.
• Use the following Fourier correspondence, where  ${\rm \Delta} (t)$  denotes a triangular pulse symmetric about  $t = 0$  with  ${\rm \Delta} (t= 0) = 1$  and  ${\rm \Delta} (t) = 0$  for  $|t| \ge T$:

$${\rm \Delta} (t) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} T \cdot {\rm si}^2 ( \pi f T).$$

Questions

1

What is the discrete ACF value of the source symbols for  $k = 0$?

$\varphi_q(k=0) \ = \ $

2

Which statements are valid for the PSD functions  ${\it \Phi}_q(f)$  and  ${\rm P} \{ {\it \Phi}_q(f) \}$?

	${\rm P} \{ {\it \Phi}_q(f) \}$  is a constant for all frequencies.
	${\it \Phi}_q(f)$  is constant for  $|f \cdot T| < 0.5$  and outside zero.
	${\it \Phi}_q(f)$  is  $\rm sinc^2$-shaped.

3

The source symbol sequence is  $\langle q_\nu \rangle = \langle +1, -1, +1, +1, -1, +1, +1, -1, -1, -1 \rangle$.
What are the code symbols  $c_\nu$ ? Enter the code symbol  $c_6$ .

$c_6 \ = \ $

4

What is the discrete ACF value of the code symbols for  $k = 0$.

$\varphi_c(k=0) \ = \ $

5

Calculate the ACF values  $\varphi_c(k=+1)$  and  $\varphi_c(k=-1)$.

$\varphi_c(k=+1) \ = \ $

$\varphi_c(k=-1) \ = \ $

6

What power-spectral density  ${\it \Phi}_c(f)$  results for frequencies $f=0$  and $f = 500 \hspace{0.08cm} \rm kHz$.  
Note:   For  $|k| \ge 2$   ⇒   all ACF–values  $\varphi_c(k) = 0$.

${\it \Phi}_c(f = 0) \ = \ $ $\ \cdot 10^{-6} \ \rm 1/Hz$

${\it \Phi}_c(f = 500 \hspace{0.08cm} \rm kHz)\ = \ $ $\ \cdot 10^{-6} \ \rm 1/Hz$

Solution

Solution

(1)  The discrete ACF value for  $k = 0$  gives the variance of the source symbols.

• Since  $q_\nu$  can only take the values  $-1$  and  $+1$   ⇒   $\varphi_q(k=0)\hspace{0.15cm}\underline{= 1}$.

(2)  Correct are the proposed solutions 1 and 3:

• The discrete-time ACF and its Fourier transform are:

$${\rm A} \{ \varphi_q ( \tau ) \} = \varphi_q ( k = 0) \cdot T \cdot \delta (\tau) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{\it \Phi_q}( f) \} = \varphi_q ( k = 0) \cdot T = T.$$

• It is considered that  $\varphi_q(k=0)= \sigma_q^2= 1$.  This means:   The periodic continuation of  ${\rm P} \{ {\it \Phi}_q(f) \}$  thus gives the same value for all frequencies.
• In contrast, the continuous-time ACF can be represented as follows:  

$$\varphi_q ( \tau ) = {\rm A} \{ \varphi_q ( \tau ) \} \star ( {\rm \delta} ( \tau) / T ).$$

• The associated power-spectral density  (Fourier transform of the ACF)  is then the product of the Fourier transforms of the two convolution terms:  

$${\it \Phi_q} ( f) = {\rm P} \{ {\it \Phi_q}( f) \} \cdot {\rm sinc}^2 (f T ) = T \cdot {\rm sinc}^2 (f T ) .$$

• Based on the chosen ACF interpolation  (with straight line intercepts)  from their samples, a  $\rm sinc^2$-shaped PSD is obtained.
• A rectangular spectrum according to the second proposed solution would only occur with  $\rm sinc$-shaped interpolation.

(3)  The coded sequence is:   $\langle +1, \ 0, -1, +1, \ 0, -1, +1, \ 0, \ 0, \ 0 \rangle$.  Thus the 6th code symbol is  $c_6\hspace{0.15cm}\underline{= -1}$.

(4)  The occurrence probabilities of the values  $-1$,   $\ 0$   and  $+1$  are  $0.25,   0.5,   0.25$.  It follows:

$$\varphi_c ( k = 0) = 0.25 \cdot (-1)^2 + 0.5 \cdot 0^2 +0.25 \cdot (+1)^2\hspace{0.15cm}\underline{ = 0.5}.$$

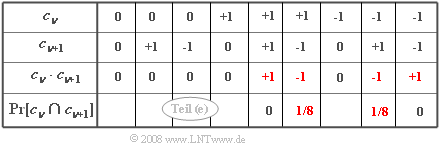
(5)  For the ACF value at  $k = 1$  consider the product  $c_{\nu} \cdot c_{\nu+1}$.  The combinations shown in the table are obtained.

• Only products  $c_{\nu} \cdot c_{\nu+1} \ne 0$  with  ${\rm Pr}\big[c_{\nu} \cdot c_{\nu+1}\big] \ne 0$:

$$\varphi_c ( k = 1) = {\rm Pr} \big [( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \big ] \cdot (+1) \cdot (-1) + {\rm Pr} \big [ ( c_{\nu} = -1) \cap ( c_{\nu + 1} = +1) \big ] \cdot (-1) \cdot (+1).$$

For ACF calculation of AMI code

• In the table,  these terms are marked in red.  Further:

$${\rm Pr} \big [ ( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \big ] =$$

$$= {\rm Pr} ( c_{\nu} = +1) \cdot {\rm Pr} \left ( c_{\nu + 1} = -1 | c_{\nu } = +1) \right ) = \frac{1}{4} \cdot \frac{1}{2}= \frac{1}{8} .$$

It is assumed that  $+1$  occurs with probability  $0.25$  and is followed by  $-1$  only in half of the cases.

• The same result is obtained for the second contribution. Thus applies:

$$\varphi_c ( k = 1) = \frac {1}{8} \cdot (+1)\cdot (-1) + \frac {1}{8} \cdot (-1)\cdot (+1) \hspace{0.15cm}\underline{= -0.25}.$$

$$\varphi_c ( k = -1) = \varphi_c ( k = 1) \hspace{0.15cm}\underline{= -0.25}.$$

• To calculate  $\varphi_c ( k = 2)$  it is necessary to average over  $3^3 = 27$  combinations. The result is zero.

(6)  The Fourier transform of the discrete-time ACF  ${\rm A} \{ \varphi_c(\tau) \}$  is:

$$P \{{\it \Phi_c}( f) \} = T\cdot \varphi_c ( k = 0) +2T \cdot \varphi_c ( k = 1) \cdot {\rm cos} ( 2 \pi f T ).$$

• With the result of the last subtask,  it follows:

$$P \{{\it \Phi}_c( f) \} = \frac {T}{2} (1 - {\rm cos} ( 2 \pi f T ) )= T \cdot {\rm sin}^2 ( \pi f T ).$$

• As shown in item  (2):  For the PSD – that is, the Fourier transform of  $\varphi_c(\tau)$:

$${\it \Phi_c}( f) = T \cdot {\rm sin}^2 ( \pi f T ) \cdot {\rm sinc}^2 ( f T ) = T \cdot \frac {{\rm sin}^4 ( \pi f T )}{( \pi f T )^2 } .$$

$$\Rightarrow \hspace{0.3cm} {\it \Phi_c}( f = 0) \hspace{0.15cm}\underline{= 0}, \hspace{0.8cm} {\it \Phi_c}( f = {\rm500 \hspace{0.1cm}kHz}) = T \cdot \frac {{\rm sin}^4 ( \pi /2 )}{( \pi /2 )^2 } = \frac {4 T}{\pi^2} \rm \hspace{0.15cm}\underline{= 0.405 \cdot 10^{-6} \ {1}/{Hz}}.$$