Exercise 4.14: ACF and CCF for Square Wave Signals
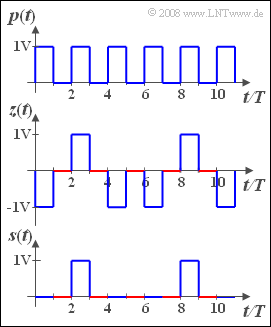
We consider a periodic square wave signal p(t) corresponding to the top sketch with the two possible amplitude values 0V and 1V and the rectangle duration T. Thus, the period duration is T0=2T.
Below this is drawn the random signal z(t):
- This is z(t)=0V between (2i−1)⋅T and 2i⋅T respectively (highlighted in red in the figure).
- In the intervals drawn in blue between 2i⋅T and (2i+1)⋅T the signal value is two-point distributed (±1V).
The probability that in the intervals shown in blue z(t)=+1V holds is generally equal p and independent of the previously selected values.
The lowest signal in the adjacent graph can be constructed from the first two. It holds:
- s(t)=1/2⋅[p(t)+z(t)].
- In the time intervals drawn in red between (2i−1)⋅T and 2i⋅T (i integer) holds s(t)=0V, since here both p(t) and z(t) are equal to zero.
- In the intervening intervals, the amplitude value is two-point distributed between 0V and 1V, where the value 1V occurs again with probability p.
- Or in other words: The signals z(t) and s(t) are equivalent pattern signals of the identical random process with bipolar (−1V, +1V) resp. unipolar (0V, 1V) signal representation.
Hints:
- The exercise belongs to the chapter Cross-Correlation Function and Cross Power-Spectral Density.
- Refer is also made to the chapter Auto-Correlation Function.
- Sketch the sought correlation functions in each case in the range from −7T to +7T.
Questions
Solution
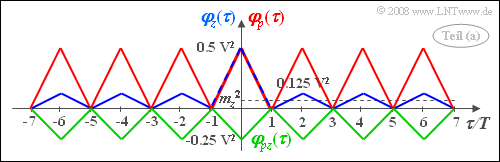
- φz(τ=0)=1/2⋅(1V)2=0.5V2_.
- For τ=±T, τ=±3T_, ... results φz(τ)=0_.
- For intermediate values τ=±2T, τ=±4T, τ=±6T_, ... applies:
- φz(τ)=1V22(p⋅p+p⋅(p−1)+(p−1)⋅p+(p−1)⋅(p−1))=...=0.5V2⋅(1−2p)2.
- Here p stands for p⋅(+1) and (p−1) for (1−p)⋅(−1), i.e. probability times normalized amplitude value, respectively.
- With p=0.25 one gets φz(τ=±6T)=0.125V2_.
The blue curve shows φz(τ) for p=0.25 in the range of −7T≤τ≤+7T:
- Because of the rectangular signal waveform, a sum of triangular functions is obtained.
- For p=0.5 the outer (smaller) triangles would disappear.
(2) The ACF φp(τ) of the unipolar periodic signal p(t) is in the generalized representation of (1) ⇒ ACF φz(τ) as a special case for p=1 .
- Now one obtains a periodic ACF (see red curve in the above sketch) with
- φp(τ=0)=φp(τ=±2T)=φp(τ=±4T)=...=0.5V2_,
- φp(τ=±T)=φp(τ=±3T)=...=0_.
(3) For the cross-correlation function results for τ=±T, τ=±3T_, ... always the value zero.
- In contrast, the CCF values for τ=±2T, τ=±2T, ... identical to those for τ=0:
- φpz(τ=0)=φpz(τ=±2T)=φpz(τ=±4T)=...=1V22(p−(1−p))=2p−12V2.
- You get the following results with p=0.25 (see green curve in above sketch):
- φpz(τ=0)=−0.25V2_,φpz(τ=3T)=0_,φpz(τ=6T)=−0.25V2_.
- With p=1 on the other hand z(t)≡p(t) would hold and so of course φpz(τ)≡φp(τ)≡φz(τ).
- For the special case p=0.5 there would be no correlation between p(t) and z(t) and thus φpz(τ)≡0.
(4) Substituting c(t)=a(t)+b(t) into the general ACF definition yields:
- φc(τ)=¯c(t)⋅c(t+τ)=¯a(t)⋅a(t+τ)+¯a(t)⋅b(t+τ)+¯b(t)⋅a(t+τ)+¯b(t)⋅b(t+τ).
- ⇒φc(τ)=φa(τ)+φab(τ)+φba(τ)+φa(τ).
- The correct solution is thus the proposed solution 2.
- The proposed solution 1 is true only if a(t) and b(t) are uncorrelated.
- The last proposition: The convolution operation is always false.
- A similar equation would result only if we consider the PDF fc(c) of the sum c(t)=a(t)+b(t) and a(t) and b(t) are statistically independent:
- fc(c)=fa(a)⋆fb(b).
(5) Using the result from (4) and taking into account the factor 1/2 we get:
- φs(τ)=1/4⋅[φp(τ)+φz(τ)+2⋅φpz(τ)].
- This already takes into account that the CCF between p(t) and z(t) is an even function, so that φpz(τ)=φzp(τ) holds.
- For τ=0 one therefore obtains in general with the above results:
- φs(τ=0)=1/4⋅(0.5V2+0.5V2+2⋅2p−12V2).
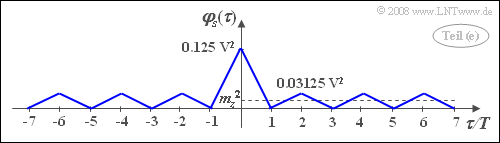
- With p=0.25 we get φpz(τ=0)=0.125V2. This result is plausible. On average, only in every eighth interval s(t)=1V; otherwise s(t)=0V.
- For even multiples of T holds:
- φs(τ=±2T)=φs(τ=±4T)= ...=0.5V24((1−2p)2+1+2⋅(2p−1))=0.5V2⋅p2.
- With p=0.5 we obtain for this the value 0.03125V2. All ACF values at odd multiples of T are zero again.
- This gives the outlined ACF–curve.
Thus, the numerical values we are looking for are:
- φs(τ=0)=0.125V2_,
- φs(τ=3T)=0_,
- φs(τ=6T)=−0.03125V2_.
A comparison with the sketch for subtask (1) shows that the binary signal s(t) has the same ACF as the ternary signal z(t) except for the factor 1/4.