Exercise 1.10: BPSK Baseband Model

• Return to book

Unbalanced channel frequency response

In this exercise,  we consider a BPSK system with coherent demodulation,  i.e.

$$s(t) \ = \ z(t) \cdot q(t),$$

$$b(t) \ = \ 2 \cdot z(t) \cdot r(t) .$$

The designations chosen here are based on the  "block diagram"  in the theory section.

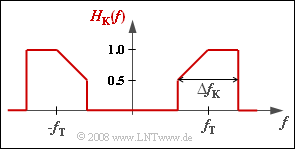
The influence of a channel frequency response  $H_{\rm K}(f)$  can be taken into account in a simple way if it is described together with modulator and demodulator by a common baseband frequency response:

$$H_{\rm MKD}(f) = {1}/{2} \cdot \big [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\big ] .$$

• Thus the modulator and demodulator are virtually shortened against each other,  and

• the band-pass channel  $H_{\rm K}(f)$  is transformed into the low-pass range.

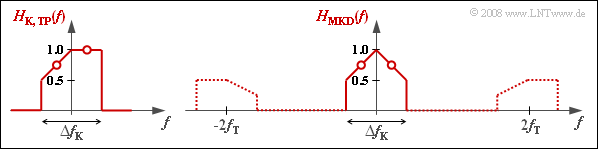
The resulting transmission function  $H_{\rm MKD}(f)$  should not be confused with the low-pass transmission function  $H_{\rm K, \, TP}(f)$  as described in the chapter  "Equivalent Low-Pass Signal and its Spectral Function"  of the book "Signal Representation",  which results from  $H_{\rm K}(f)$  by truncating the components at negative frequencies as well as a frequency shift by the carrier frequency $f_{\rm T}$  to the left.

For frequency responses,  in contrast to spectral functions,  the doubling of the components at positive frequencies must be omitted.

Notes:

• The exercise belongs to the chapter  "Linear Digital Modulation - Coherent Demodulation".

• Reference is made in particular to the section  "Baseband model for ASK and BPSK".

• The subscript  "MKD"  stands for  "modulator – channel – demodulator"  German:  "Modulator – Kanal – Demodulator").

Questions

1

Which statements are valid for the equivalent low-pass function  $H_{\rm K, \, TP}(f)$ ?

	$H_{\rm K, \, TP}(f=0)= 2$.
	$H_{\rm K, \, TP}(f = \Delta f_{\rm K}/4) = 1$.
	$H_{\rm K, \, TP}(f = -\Delta f_{\rm K}/4) = 0.75$.
	The corresponding time function  $h_{\rm K, \, TP}(t)$  is complex.

2

Which statements are valid for the frequency response  $H_{\rm MKD}(f)$ ?

	$H_{\rm MKD}(f=0)= 2$.
	$H_{\rm MKD}(f = \Delta f_{\rm K}/4) = 1$.
	$H_{\rm MKD}(f = -\Delta f_{\rm K}/4) = 0.75$.
	The corresponding time function  $h_{\rm MKD}(t)$  is complex.

3

Calculate the time function  $h_{\rm MKD}(t)$.  Specify the value at  $t = 0$. 

$h_{\rm MKD}(t = 0)/\Delta f_{\rm K} \ = \ $

4

Which of the following statements are true?

	$h_{\rm MKD}(t)$  has equidistant zero crossings at distance  $1/\Delta f_{\rm K}$.
	$h_{\rm MKD}(t)$  has equidistant zero crossings at distance  $2/\Delta f_{\rm K}$.

Solution

Solution

(1)  Statements 2, 3 and 4  are correct:

• $H_{\rm K,TP}(f)$  results from  $H_{\rm K}(f)$  by cutting off the negative frequency components and shifting  $f_{\rm T}$  to the left.

• For frequency responses  – in contrast to spectra –  the doubling of the components at positive frequencies is omitted.  Therefore:

$$H_{\rm K,\hspace{0.04cm} TP}(f= 0) = H_{\rm K}(f= f_{\rm T})=1.$$

• Because of the real and asymmetrical spectral functions  $H_{\rm K,\hspace{0.04cm}TP}(f),$  the corresponding time function  (inverse Fourier transform)  $h_{\rm K,\hspace{0.04cm}TP}(t)$  is complex according to the  "Allocation Theorem".

Low-pass functions for  $H_{\rm K}(f)$

(2)  Here only the  third proposed solution  is correct:

• The spectral function  $H_{\rm MKD}(f)$  always has an even real part and no imaginary part.  Consequently  $h_{\rm MKD}(t)$  is always real.

• If  $H_{\rm K}(f)$  had additionally an imaginary part odd by $f= f_{\rm T}$,  $H_{\rm MKD}(f)$  would have an imaginary part odd by $f = 0$.  Thus  $h_{\rm MKD}(t)$  would still be a real function.

The diagram illustrates the differences between  $H_{\rm K,\hspace{0.04cm}TP}(f)$  and  $H_{\rm MKD}(f)$.  The parts of  $H_{\rm MKD}(f)$  in the range around  $\pm 2f_{\rm T}$  need not be considered further.

(3)  $H_{\rm MKD}(f)$  is additively composed of a rectangle and a triangle,  each with width  $\Delta f_{\rm K}$  and height  $0.5$. It follows:

$$h_{\rm MKD}(t) = \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} ( \Delta f_{\rm K} \cdot t)+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 ( \frac{\Delta f_{\rm K}}{2} \cdot t)$$

$$\Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0) = \frac{\Delta f_{\rm K}}{2} + \frac{\Delta f_{\rm K}}{4} = 0.75 \cdot \Delta f_{\rm K}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0)/{\Delta f_{\rm K}} \hspace{0.1cm}\underline {= 0.75} .$$

(4)  The  second proposed solution  is correct:

• The first sinc–function does have equidistant zero crossings at the distance  $1/\Delta f_{\rm K}$.
• But the equidistant zero crossings of the whole time function  $h_{\rm MKD}(t)$  are determined by the second term:

$$h_{\rm MKD}(t = \frac{1}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} (1 )+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 (0.5) = \frac{\Delta f_{\rm K}}{4},$$

$$h_{\rm MKD}(t = \frac{2}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} (2 )+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 (1) = 0.$$