Exercise 4.11: On-Off Keying and Binary Phase Shift Keying

• Return to book

Two signal space constellations for OOK and BPSK

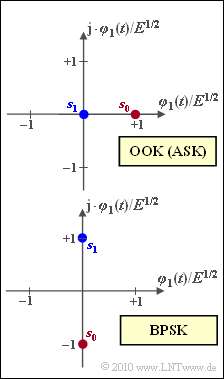
The graphic shows signal space constellations for carrier-modulated modulation methods:

• "On–Off Keying"  $\rm (OOK)$,  also known as  "Amplitude Shift Keying"  $\rm (ASK)$  in some books,

• "Binary Phase Shift Keying"  $\rm (BPSK)$.

For the error probability calculation we start from the AWGN channel.  In this case the error probability is 
$($related to symbols or to bits alike$)$:

$$p_{\rm S} = p_{\rm B} = {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right ) \hspace{0.05cm}.$$

Here

• $d$  denotes the distance between the signal space points,  and

• $\sigma_n^2 = N_0/2$  the variance of the AWGN noise.

In the questions from  (3)  onwards,  reference is also made to the mean symbol energy  $E_{\rm S}$. 

Notes:

• The exercise belongs to the chapter  "Carrier Frequency Systems with Coherent Demodulation".

• Reference is also made to the chapter  "Linear Digital Modulation – Coherent Demodulation"  and the chapter  "Linear Digital Modulation"  in the book  "Modulation Methods".

• For the complementary Gaussian error function,  use the following approximation:

$${\rm Q}(x) \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$

Questions

1

How many bits  $(b)$  does each symbol represent?  What is the level number  $M$?

$b \hspace{0.35cm} = \ $

$M \ = \ $

2

Which representation do the signal space constellations show?

	The representation in the (actual) band-pass range,
	the representation in the (equivalent) low-pass range.

3

What error probability results for  "On–Off Keying"  depending on  $E_{\rm S}/N_0$?

$E_{\rm S}/N_0 = 9 \text{:} \hspace{2.3cm} p_{\rm S} \ = \ $ $\ \cdot 10^{\rm –4}$

$10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 12 \ {\rm dB} \text{:} \hspace{0.2cm} p_{\rm S} \ = \ $ $\ \cdot 10^{\rm –4}$

4

What is the error probability for  "Binary Phase Shift Keying"  depending on  $E_{\rm S}/N_0$?

$E_{\rm S}/N_0 = 9 \text{:} \hspace{2.3cm} p_{\rm S} \ = \ $ $\ \cdot 10^{\rm –8}$

$10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 12 \ {\rm dB} \text{:} \hspace{0.2cm} p_{\rm S} \ = \ $ $\ \cdot 10^{\rm –8}$

Solution

Solution

(1)  Both  "'On–Off Keying"  $\rm (OOK)$  and  "Binary Phase Shift Keying"  $\rm (BPSK)$  are binary modulation methods:

$$\underline{b = 1 }\hspace{0.05cm},\hspace{0.5cm} \underline{M = 2} \hspace{0.05cm}.$$

(2)  Solution 2  is correct,  recognizable by the imaginary basis function  $\varphi_2(t) = {\rm j} \cdot \varphi_1(t)$.

• If described in the band-pass range,  the basis functions would be real:  "cosine"  and  "(minus) sine".

(3)  The given equation is for  "On–Off Keying"  with

• $d = \sqrt {E}$,

• $E_{\rm S} = E/2$  (assuming equally probable symbols  $\boldsymbol{s}_0$  and  $\boldsymbol{s}_1$),

• $\sigma_n^2 = N_0/2$:

$$p_{\rm S} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right )= {\rm Q} \left ( \frac{ \sqrt{E}/2}{ \sqrt{N_0/2}}\right ) = {\rm Q} \left ( \sqrt{ \frac{ E/2}{ N_0} }\right ) = {\rm Q} \left ( \sqrt{ { E_{\rm S}}/{ N_0} }\right ) \hspace{0.05cm}.$$

• For  $E_{\rm S}/N_0 = 9 = 3^2$  this results in:

$$p_{\rm S} = {\rm Q} (3) \approx \frac{1}{\sqrt{2\pi} \cdot 3} \cdot {\rm e}^{-9/2} = \underline{14.8 \cdot 10^{-4}} \hspace{0.05cm}.$$

• Accordingly,  for  $10 \cdot {\rm lg} \, (E_{\rm S}/N_0) = 12 \ \rm dB$   ⇒   $E_{\rm S}/N_0 = 15.85$:

$$p_{\rm S} = {\rm Q} (\sqrt{15.85}) \approx \frac{1}{\sqrt{2\pi\cdot 15.85} } \cdot {\rm e}^{-15.85/2} = \underline{0.362 \cdot 10^{-4}} \hspace{0.05cm}.$$

(4)  In contrast to subtask  (3),  "Binary Phase Shift Keying" $\rm (BPSK)$  applies

• $d = 2 \cdot \sqrt {E}$,

• $E_{\rm S} = E$,

both even independent of the occurrence probabilities for  $\boldsymbol{s}_0$  and  $\boldsymbol{s}_1$.

• It follows:

$$p_{\rm S} = {\rm Q} \left ( \frac{ \sqrt{E_{\rm S}}}{ \sqrt{N_0/2}}\right ) = {\rm Q} \left ( \sqrt{ { 2E_{\rm S}}/{ N_0} }\right ) \hspace{0.05cm}.$$

• With  $E_{\rm S}/N_0 = 9$,  this results in the numerical value:

$$p_{\rm S} = {\rm Q} (\sqrt{18}) \approx \frac{1}{\sqrt{2\pi\cdot 18} } \cdot {\rm e}^{-18/2} = \underline{117 \cdot 10^{-8}} \hspace{0.05cm}.$$

• And with  $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 12 \ \rm dB$   ⇒   $2E_{\rm S}/N_0 = 31.7$:

$$p_{\rm S} = {\rm Q} (\sqrt{31.7}) \approx \frac{1}{\sqrt{2\pi\cdot 31.7} } \cdot {\rm e}^{-31.7/2} = \underline{0.926 \cdot 10^{-8}}\hspace{0.05cm}.$$