Exercise 2.7: Huffman Application for Binary Two-Tuples

• Return to book

Three binary codes for  $M = 4$

The application of the Huffman algorithm in its original form assumes a symbol set size  $M > 2$  and is therefore useless for data compression of binary sources.

However, if one combines several consecutive binary characters of the source into a new symbol, one can usefully apply Huffman data compression to the new symbol set.

In this task we start from the source symbol set  $\{$ $\rm X$,  $\rm Y$ $\}$   ⇒   $M = 2$  and form two-tuples according to the table on the right with the new symbol set  $\{$ $\rm A$,  $\rm B$,  $\rm C$,  $\rm D$ $\}$  ⇒  $(M\hspace{0.03cm}' = M^2 = 4)$. 

For example, the binary source symbol sequence  $\rm XYXXYXXXYY$  thus becomes the quaternary sequence  $\rm BACAD$.

Furthermore, three codes are given in the table, some of which have been created by the Huffman algorithm.  The binary output sequences then result for our example as follows:

• $\text{Code 1}$:   1011011100,
• $\text{Code 2}$:   0110011000,
• $\text{Code 3}$:   10011001110.

Again for understanding:

• From the original symbol set  $\{$ $\rm X$,  $\rm Y$ $\}$  a quaternary set with symbol set  $\{$ $\rm A$,  $\rm B$,  $\rm C$,  $\rm D$ $\}$ is obtained by forming two-tuples. 
• The sequence length $N$ is thereby halved to  $N\hspace{0.03cm}' = N/2$ .
• Huffman coding again results in a binary sequence whose symbol set is designated  $\{$0,  1$\}$  for better differentiation.
• The application of Huffman coding makes sense exactly when the length  $L$  of the initial sequence is smaller than  $N$ (on statistical average).

This task is intended to clarify which of the given binary codes make sense under which boundary conditions.

• Let the binary message source  $\{$ $\rm X$,  $\rm Y$ $\}$  be memoryless and be described solely by the symbol probability  $p_{\rm X}$ .
• The second probability is then always  $p_{\rm Y} = 1 - p_{\rm X}$.

Hints:

• The exercise belongs to the chapter  Entropy Coding according to Huffman.
• In particular, reference is made to the page  Application of Huffman coding to  $k$-tuples.
• The average code word length per two-tuple is  $L_{\rm M}\hspace{0.03cm}' = p_{\rm A} \cdot L_{\rm A} +$  ...  $+ p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm}$.  With respect to a source symbol,  $L_{\rm M} = L_{\rm M}\hspace{0.03cm}'/2$.
• A comparable task with ternary input symbols is treated in  Exercise 2.7Z .

• The idea for this task arose during a lecture by  Prof. Robert Fischer  from the University of Ulm at the Technical University of Munich on the topic of
      "Der goldene Schnitt in der Nachrichtentechnik"   ⇒   "The golden ratio in communications technology".

Questions

1

Give the average code word lengths with redundancy-free binary source.

$\text{Code 1}$:   $L_{\rm M} \ = \ $ $\ \rm bit/source\hspace{0.15cm}symbol$

$\text{Code 2}$:   $L_{\rm M} \ = \ $ $\ \rm bit/source\hspace{0.15cm}symbol$

$\text{Code 3}$:   $L_{\rm M} \ = \ $ $\ \rm bit/source\hspace{0.15cm}symbol$

2

Determine the Huffman code with respect to two-tuples for  $p_{\rm X}= 0.6$.

	The result is  $\text{Code 1}$.
	The result is  $\text{Code 2}$.
	The result is  $\text{Code 3}$.

3

What is the average code word length of the best Huffman code for  $p_{\rm X}= 0.6$ ?

$L_{\rm M} \ = \ $ $\ \rm bit/source\hspace{0.15cm}symbol$

4

Determine the Huffman code with respect to two-tuple for  $p_{\rm X}= 0.8$.

	The result is  $\text{Code 1}$.
	The result is  $\text{Code 2}$.
	The result is  $\text{Code 3}$.

5

What is the average code word length of the best Huffman code for  $p_{\rm X}= 0.8$ ?

$L_{\rm M} \ = \ $ $\ \rm bit/source\hspace{0.15cm}symbol$

6

In what range may the probability  $p_{\rm X}$  for the symbol  $\rm X$  lie so that the  $\text{Code 1}$  results according to Huffman?

$p_\text{X, min}\ = \ $

$p_\text{X, max}\ = \ $

Solution

Solution

(1)  With redundancy-free binary source  $(p_{\rm X} = p_{\rm Y} = 0.5)$  one obtains  $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 0.25$  and with the given equation:

$$L_{\rm M} = \big [ \hspace{0.05cm}p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B} + p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm} \big ] / 2 = \big [ \hspace{0.05cm} L_{\rm A} + L_{\rm B} + L_{\rm C} + L_{\rm D}\hspace{0.05cm} \big ] / 8 \hspace{0.05cm}.$$

Taking into account the given assignments, we obtain for

• $\text{Code 1}$:    $L_{\rm M} \hspace{0.15cm}\underline{= 1.000 \ {\rm bit/source \hspace{0.15cm}symbol} }$,
• $\text{Code 2}$:    $L_{\rm M} \hspace{0.15cm}\underline{= 1.125 \ {\rm bit/source \hspace{0.15cm}symbol} }$,
• $\text{Code 3}$:    $L_{\rm M} \hspace{0.15cm}\underline{= 1.250 \ {\rm bit/source \hspace{0.15cm}symbol} }$.

In the course of the task it will become apparent that the first two codes are quite possible as a result of the Huffman algorithm (of course only with suitable symbol probabilities).   $\text{Code 3}$  is also prefix-free, but never optimal in terms of average code word length.

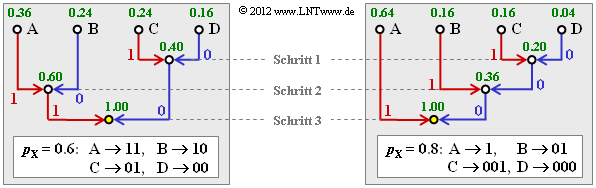
(2)  The probabilities of the possible two-tuples are:

$$p_{\rm A} = 0.6^2 = 0.36 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.6 \cdot 0.4 = 0.24 = p_{\rm C} \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.4^2 = 0.16 \hspace{0.05cm}.$$

• This gives the  tree diagram on the left  (in the adjacent graph) and the following Huffman code:

Huffman tree diagram for two different two-tuple constellations  ("Schritt"   ⇒   EN:  "step")

    $\rm A$   →   11,   $\rm B$   →   10,   $\rm C$   →   01,   $\rm D$   →   00.

• This is  $\text{Code 1}$   ⇒   solution suggestion 1.

(3)  Each two-tuple is represented by two bits.  Thus

$$L_{\rm M} \hspace{0.15cm}\underline{= 1.000 \ {\rm bit/source \hspace{0.15cm}symbol} }.$$

(4)  Here the probabilities of each two-tuple are:

$$p_{\rm A} = 0.8^2 = 0.64 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.8 \cdot 0.2 = 0.16 \hspace{0.05cm},$$

$$p_{\rm C} = p_{\rm B}= 0.8 = 0.16 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.2^2 = 0.04 \hspace{0.05cm}.$$

According to the tree diagram on the right the result is now  $\text{Code 2}$   ⇒   solution suggestion 2:

    $\rm A$   →   1,   $\rm B$   →   01,   $\rm C$   →   001,   $\rm D$   →   010.

(5)  For  $\text{Code 2}$  the mean two-tuple length or the average code word length is:

$$L_{\rm M}\hspace{0.01cm}' = 0.64 \cdot 1 + 0.16 \cdot 2 + (0.16 + 0.04) \cdot 3 = 1.56\,{\rm bit/two-tuples}\hspace{0.3cm} \Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{2}\hspace{0.15cm}\underline{ = 0.78\,{\rm bit/source \:symbol}}\hspace{0.05cm}.$$

(6)  From the earlier subtasks it has been found:

• For  $p_{\rm X} = 0.6$,    $\text{Code 1}$  is optimal and the average code word length of this code is  $($independent of  $p_{\rm X})$  $L_{\rm M} = 1$  bit/source  symbol.
• For  $p_{\rm X} = 0.8$  according to subtask  (4),  $\text{Code 2}$  is optimal and the average code word length is  $L_{\rm M} = 0.78$  bit/source  symbol.

The sought maximum value  $p_\text{X, max}$  will thus lie between  $0.6$  and  $0.8$ .  The determining equation here is that for the limiting case  $p_\text{X} = p_\text{X, max}$  both codes have exactly the same average code word length  $L_{\rm M} = 1$  bit/source  symbol, or  $L_{\rm M}\hspace{0.03cm}' = 2$  bit/two-tuple.

• With the abbreviation  $p = p_\text{X, max}$  the corresponding determining equation is:

$$L_{\rm M}\hspace{0.01cm}'\hspace{0.15cm}{\rm (Code \hspace{0.15cm}2)} = p^2 \cdot 1 + p \cdot (1-p) \cdot 2 + p \cdot (1-p) \cdot 3 + (1-p)^2 \cdot 3 \stackrel{!}{=} 2 \hspace{0.05cm}.$$

• This leads to the numerical result:

$$p^2 + p - 1 \stackrel{!}{=} 0 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} p_{\rm X,\hspace{0.05cm}max} = p = \frac{\sqrt{5}-1}{2} \hspace{0.15cm}\underline{ \approx 0.618} \hspace{0.05cm}.$$

• Since the basic Huffman structure does not change by swapping  $\rm X$  and  $\rm Y$  the lower bound is:

$$p_{\rm X,\hspace{0.05cm}min} = 1 - p_{\rm X,\hspace{0.05cm}max}\hspace{0.15cm}\underline{ \approx 0.382} \hspace{0.05cm}.$$

The representation of the tuples of two by bit sequences of different lengths  $\text{(Code 2)}$  therefore only makes sense if the symbol probabilities of  $\rm X$  and  $\rm Y$  differ significantly.  If, on the other hand, they are between  $0.382$  and  $0.618$,  $\text{Code 1}$  is to be applied.

Note:     The division of a path of length   $1$  into two sections of length  $0.618$...  and  $0.382$...  is called the  Golden ratio, which is encountered again and again in the most diverse fields.