Exercise 1.7: Coding for Broadband ISDN

• Return to book

HDB3 and 1T2B coding

For conventional ISDN over copper lines the  $\rm HDB3$  ("High Definition Bipolar")  code is used – see  $\text{Exercise 1.5}$:

This was derived from the so-called  "AMI code",

• is like the latter a pseudo-ternary code,

• but avoids more than three consecutive  "$0$"  symbols,

• by deliberately violating the stricter AMI coding rule for longer zero sequences.

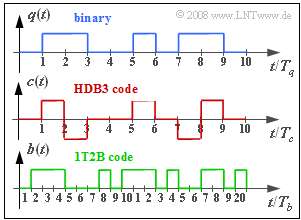
The graph shows the HDB3 encoded signal  $c(t)$  resulting from the binary redundancy-free source signal  $q(t)$.  Since there are no more than three consecutive zeros in the source signal,  $c(t)$  is identical to the AMI-encoded signal.

The broadband ISDN planned for the late 1990s was to provide data rates of up to  $\text{155 Mbit/s}$  compared with  $\text{144 kbit/s}$  of conventional ISDN with two bearer channels and one data channel.  To achieve this higher data rate,  it was necessary that

• newer technology  $\rm (ATM)$  had to be used,

• secondly,  the transmission medium had to be changed from copper to fiber optics.

However,  since the HDB3-encoded signal  $c(t) ∈ \{–1, \ 0, +1\}$  cannot be transmitted by means of light,  a second encoding was required. 

1. The  1T2B code  provided for this purpose replaces each ternary symbol with two binary symbols. 
2. The lower diagram shows an example of the binary signal  $b(t) ∈ \{0, 1\}$,  which results from the signal  $c(t)$  after this 1T2B coding.
3. For this exercise,  assume that the bit rate of the redundancy-free source signal  $q(t)$  is equal to  $R_{q} = 2.048 \ \rm Mbit/s$. 
4. The respective symbol durations of the signals  $q(t),  c(t)$  and  $b(t)$  are denoted by  $T_{q}$,  $T_{c}$  and  $T_{b}$. 
5. The equivalent bit rate of the pseudo-ternary signal  $c(t)$  is  $R_{c} = {\rm log_2}(3)/T_{c}$,  from which the bit rate  $R_{q} = 1/T_{q}$  of the source signal can be used to calculate the relative redundancy of the AMI or HDB3 code:

$$r_{\rm HDB3} = \frac{R_c - R_q}{R_c}= 1 - \frac{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_c)} \hspace{0.05cm}.$$

A similar equation can be established for the 1T2B code,  as well as for the two codes in combination.

Notes:

• The exercise belongs to the chapter  "Further Developments of ISDN".

• Redundancy is defined and illustrated with examples in the chapter  "Basics of Coded Transmission"  of the book "Digital Signal Transmission".

Questions

1

What is the assignment of the  1T2B code?

	$c(t) = +1 \Rightarrow b(t) = 10, \hspace{1cm}c(t) = 0 \Rightarrow b(t) = 00, \hspace{1cm}c(t) = -1 \Rightarrow b(t) = 01,$
	$c(t) = +1 \Rightarrow b(t) = 11, \hspace{1cm}c(t) = 0 \Rightarrow b(t) = 01, \hspace{1cm}c(t) = -1 \Rightarrow b(t) = 00,$
	$c(t) = +1 \Rightarrow b(t) = 01, \hspace{1cm}c(t) = 0 \Rightarrow b(t) = 11, \hspace{1cm}c(t) = -1 \Rightarrow b(t) = 10.$

2

What are the symbol durations of  $q(t),   c(t)$  and   $b(t)$?

$T_{q} \ = \ $ $\ \rm µ s$

$T_{c} \ = \ $ $\ \rm µ s$

$T_{b} \ = \ $ $\ \rm µ s$

3

Calculate the relative redundancy of the  HDB3 code.

$r_{\rm HDB3} \ = \ $ $\ \%$

4

Calculate the relative redundancy of the  1T2B code.

$r_{\rm 1T2B} \ = \ $ $\ \%$

5

What is the relative redundancy of the signal  $b(t)$, i.e. the  combination  of HDB3 code and 1T2B code?

$r_{\rm HDB3+1T2B} \ = \ $ $\ \%$

Solution

Solution

(1)  Solution 2  is correct,  as a comparison of the signal characteristics  $c(t)$  and  $b(t)$  shows.

(2)  The symbol duration  $(=$ bit duration$)$  of  $q(t)$  is   $T_{q} \hspace{0.15cm}\underline{ = 1/R_{q} = 0.488 \ \rm µ s}$.

• The symbol duration of the AMI code  (and the HDB3 code)  is exactly the same:   $T_{c} \hspace{0.15cm}\underline{ = 0.488 \ \rm µ s}$.

• In contrast,  the symbol duration  $(=$ bit duration$)$  after the 1T2B encoding is only half as large:  $T_{b} = T_{c}/2 \hspace{0.15cm}\underline{= 0.244 \ \rm µ s}$.

(3)  Using the given equation,  with  $M_{q} = 2, \hspace{0.15cm} M_{c} = 3$  and  $T_{c} = T_{q}$,  we get:

$$r_{\rm HDB3} = 1 - \frac{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_c)} = 1 - \frac{1}{{\rm log_2}\hspace{0.1cm}(3)} \hspace{0.15cm}\underline{= 36.9\,\%} \hspace{0.05cm}.$$

(4)  Fitting the equation to the 1T2B code,  we obtain with  $M_{c} = 3, \hspace{0.15cm} M_{b} = 2,  T_{b} = T_{c}/2$:

$$r_{\rm 1T2B} = 1 - \frac{T_b \cdot {\rm log_2}\hspace{0.1cm}(M_c)}{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_b)} = 1 - \frac{{\rm log_2}\hspace{0.1cm}(3)}{2} \hspace{0.15cm}\underline{= 20.7\,\%} \hspace{0.05cm}.$$

(5)  The resulting redundancy of both codes is obtained by relating the given equation to the input signal  $q(t)$  and the output signal  $c(t)$.

• With  $M_{q} = M_{b} = 2$  and  $T_{b} = T_{q}/2$  it follows:

$$r_{\rm HDB3+1T2B} = 1 - \frac{T_b \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_b)} = 1 - \frac{T_b}{T_q} \hspace{0.15cm}\underline{= 50\,\%} \hspace{0.05cm}.$$

• The same result is obtained by the calculation

$$1-r_{\rm HDB3+1T2B} \ = \ (1-r_{\rm HDB3}) \cdot (1-r_{\rm 1T2B}) =(1- 1 +\frac{1}{{\rm log_2}\hspace{0.1cm}(3)}) \cdot (1-1+ \frac{{\rm log_2}\hspace{0.1cm}(3)}{2}) = 50\,\% \hspace{0.05cm}.$$

$$\Rightarrow \hspace{0.3cm}r_{\rm HDB3+1T2B}= 50\,\% \hspace{0.05cm}.$$