Exercise 1.2: ISDN and PCM

• Return to book

Components of PCM transmitter

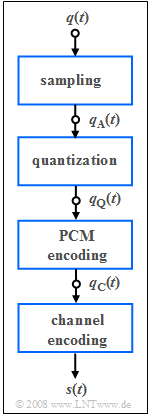
The conversion of the analog speech signal  $q(t)$  into the binary signal  $q_{\rm C}(t)$  is done at  $\rm ISDN$  ("Integrated Services Digital Network")  according to the guidelines of  "pulse code modulation"  $\rm (PCM)$  by

• sampling in the interval  $T_{\rm A} = 1/f_{\rm A}$,

• quantization to  $M = 256$  discrete values,

• binary PCM encoding with  $N$  bits per quantization value.

The net data rate of a  $\rm B$ channel  ("Bearer Channel") is  $64 \ \rm kbit/s$  and corresponds to the bit rate of the redundancy-free binary signal  $q_{\rm C}(t)$. 

However,  because of the subsequent redundant channel coding and the inserted signaling bits,  the gross data rate – i.e.,  the transmission rate of the transmitted signal  $s(t)$  – is greater.

A measure for the quality of the entire ISDN transmission system is the sink SNR

$$\rho_{v} = \frac{P_q}{P_{\varepsilon}} = \frac{\overline{q(t)^2}}{\overline{[\upsilon(t) - q(t)]^2}}$$

as the ratio of the powers

• of the analog signal  $q(t)$  bandlimited to the range  $300 \ {\rm Hz}\ \text{...}\ 3400 \ {\rm Hz}$ 

• and the error signal  $\varepsilon (t) = v (t) - q(t)$.

An ideal signal reconstruction with an ideal rectangular low-pass filter is assumed here for the sink signal  $v (t)$. 

Notes:

• The exercise refers to the chapter  "General Description of ISDN" of this book.

• Reference is also made to the chapter  "Pulse Code Modulation"  of the book  "Modulation Methods".

Questions

1

With how many bits  $(N)$  is each quantized sample represented?

$N \ = \ $

2

What is the sampling rate  $f_{\rm A}$?

$f_{\rm A} \ = \ $ $\ \rm kHz$

3

Does this satisfy the sampling theorem?

	Yes,
	no.

4

Is the sink SNR  $\rho_{v}$  at ISDN limited by the following effects?

	Sampling  (if sampling theorem is satisfied),
	AWGN noise  (transmission error).

Solution

Solution

(1)  The quantization level number  $M$  is usually chosen as a power of two and for the number of bits  $N = {\log_2}\hspace{0.05cm}(M)$.

• From  $M = 2^{8} = 256$  follows  $\underline{N = 8}$.

(2)  For the bit rate,  $R_{\rm B} = N \cdot f_{\rm A}$.

• Thus,  from  $R_{\rm B} = 64 \ \rm kbit/s$  and  $N = 8$,  we get  $f_{\rm A} \hspace{0.15cm}\underline{= 8 \ \rm kHz}$.

(3)  Due to the bandwidth limitation,  the highest frequency contained in the signal  $q(t)$  is equal to  $3.4 \ \rm kHz$.

• Therefore,  according to the sampling theorem,  $f_{\rm A} ≥ 6.8 \ \rm kHz$  should hold.

• With  $f_{\rm A} = 8 \ \rm kHz$  the condition is fulfilled   ⇒   $\underline {\rm YES}$.

(4)  The  last statement  is correct:

• Even if the influence of the AWGN noise is small  $($small noise power density  $N_{0})$,  the sink SNR  $\rho_{v}$  cannot fall below a limit given by the quantization noise:

$$\rho_{v} \approx \rho_{\rm Q} = 2^{2M} = 2^{16} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} \approx 48\, {\rm dB}\hspace{0.05cm}.$$

• With larger noise interference,  $\rho_{v}$  can further  (significantly)  be reduced by the transmission errors.

• In contrast,  sampling results in no loss of quality if the sampling theorem is obeyed.

• Sampling can then be completely undone if the source signal  $q(t)$  is bandlimited and the signal reconstruction is correctly dimensioned   ⇒   ideal low-pass.