Exercise 2.2Z: Galois Field GF(5)
Wie in der Aufgabe 2.2 betrachten wir einen endlichen Körper der Ordnung $q = 5$ und damit das Galoisfeld
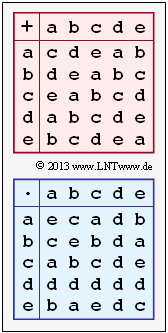
- $${\rm GF}(5) = \{{a}, { b},{c},{d},{e}\}\hspace{0.05cm}.$$
Über die Elemente werden weiter keine Aussagen getroffen. Es können sowohl ganze Zahlen sein oder irgendwelche mathematische Ausdrücke.
Das Galoisfeld wird ausschließlich bestimmt durch
- eine Additionstabelle modulo 5,
- eine Multiplikationstabelle modulo 5,
Die wichtigsten Eigenschaften eines Galoisfeldes sind auf der ersten Theorieseite zusammengestellt. Hier wird Bezug genommen auf
- das Kommutativ– und das Distributivgesetz,
- die neutralen Elemente von Addition und Multiplikation,
- die inversen Elemente von Addition und Multiplikation, sowie
- die Bestimmung primitiver Elemente.
Im vorliegenden Beispiel wäre $\beta$ ein primitives Element, wenn $\beta^2, \ \beta^3$ und $\beta^4$ (allgemein: $\beta^{q-1})$ die übrigen Elemente des Galoisfeldes $\rm GF(5)$ mit Ausnahme des Nullelementes ergeben.
Hinweise:
- Die Aufgabe bezieht ich auf das Themengebiet des Kapitels Einige Grundlagen der Algebra.
- Lassen Sie sich bitte nicht verwirren, dass im Text die Menge $ \{{a}, { b},{c},{d},{e}\}$ verwendet wird und in den Tabellen $ \rm \{{a}, { b},{c},{d},{e}\}$. Entschuldigung!
Fragebogen
Musterlösung
- $$z_i + N_{\rm A} = N_{\rm A} + z_i = z_i\hspace{0.05cm}.$$
Aus der Additionstabelle folgt $N_{\rm A} \ \underline{= d}$.
(2) Dagegen erfüllt das neutrale Element der Multiplikation $(N_{\rm M})$ für alle Elemente $z_i (i = 1,\hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ q-1)$ die folgende Bedingung:
- $$z_i \cdot N_{\rm M} = N_{\rm M}\cdot z_i = z_i\hspace{0.05cm}.$$
Aus der Multiplikationstabelle erkennt man $N_{\rm M} \ \underline{= c}$.
(3) Das Kommutativgesetz ist bei diesem Galoisfeld in beiden Fällen (Addition und Multiplikation) erfüllt, da Additionstabelle und Multiplikationstabelle jeweils symmetrisch zur Tabellendiagonalen sind.
(4) Betrachten wir zunächst den ersten Ausdruck. Bei Gültigkeit des Distributivgesetzes muss gelten:
- $$a \cdot (b+c) = a \cdot b+ a \cdot c \hspace{0.05cm}.$$
Für die linke Seite erhält man:
- $$a \cdot (b+c) = a \cdot a =e \hspace{0.05cm},$$
und für die rechte Seite:
- $$a \cdot b+ a \cdot c = c + a = e\hspace{0.05cm}.$$
Das Distributivgesetz ist hier ebenso erfüllt wie auch bei den beiden anderen vorgegebenen Ausdrücken:
- $$d \cdot (b+c) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot a =d \hspace{0.05cm}, \hspace{0.5cm}d \cdot b+ d \cdot c = d + d = d\hspace{0.05cm},$$
- $$e \cdot (a+c) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} e \cdot e =c \hspace{0.05cm}, \hspace{0.5cm}e \cdot a+ e \cdot c = b + e = c\hspace{0.05cm}.$$
Alle Lösungsvorschläge treffen zu.
(5) Das Nullelement $N_{\rm A} = d$ wird zu $N_{\rm A} = 0 \Rightarrow d = 0$, das Einselelement $N_{\rm M} = c$ zu $N_{\rm M} = 1 \Rightarrow c = 1$. Die weiteren Elemente $a, \ b$ und $e$ können modulo $5$ aus der Additionstabelle oder der Multiplikationstabelle bestimmt werden. Zum Beispiel folgt aus der ersten Zeile der Additionstabelle
- $$(a + b) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = d = 0 \hspace{0.05cm}.$$
Da sowohl $a$ als auch $b$ nicht $0$ oder $1$ sein können (da diese bereits für $c$ und $d$ vergeben sind), ergibt sich als Folgerung:
- $$a = 2, \hspace{0.1cm} b = 3 \hspace{0.5cm}{\rm oder}\hspace{0.5cm} a = 3, \hspace{0.1cm} b = 2\hspace{0.05cm}.$$
Aus der zweiten Zeile der Additionstabelle folgt beispielsweise:
- $$(b + b) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = e \hspace{0.05cm}.$$
Aus $b = 3$ ergäbe sich $e = 1$. Dies ist aber wiederum nicht möglich, da bereits $c = 1$ festgelegt wurde.
Also erhält man als Endergebnis:
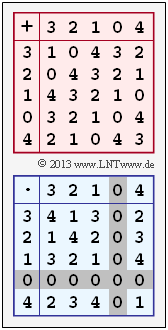
- $$a \hspace{0.15cm}\underline{= 3}\hspace{0.05cm},\hspace{0.2cm}b \hspace{0.15cm}\underline{= 2}\hspace{0.05cm},\hspace{0.2cm} c \hspace{0.15cm}\underline{= 1}\hspace{0.05cm},\hspace{0.2cm}d \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm} e \hspace{0.15cm}\underline{= 4}\hspace{0.05cm}.$$
Die Grafik zeigt die Additions– und die Multiplikationstabelle für diese Zahlenmenge.
(6) Zutreffend sind die Aussagen 1 und 4:
- Man erkennt in der Additionstabelle in jeder Zeile und Spalte genau ein $d = 0$. Das heißt: Für alle $z_i ∈ \{0, \, 1, \, 2, \, 3, \, 4\}$ existiert eine eindeutige additive Inverse.
Die multiplikative Inverse erkennt man in der Multiplikationstabelle durch den Eintrag $c = 1$. Die multiplikativen Inversen lauten wie folgt:
- $${\rm Zeile \hspace{0.15cm}1\text{:}}\hspace{0.25cm} {\rm Inv_M}(a=3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} b = 2 \hspace{0.05cm},$$
- $${\rm Zeile\hspace{0.15cm} 2\text{:}}\hspace{0.25cm} {\rm Inv_M}(b=2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} a=3 \hspace{0.05cm},$$
- $${\rm Zeile\hspace{0.15cm} 3\text{:}}\hspace{0.25cm} {\rm Inv_M}(c=1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} c=1 \hspace{0.05cm},$$
- $${\rm Zeile\hspace{0.15cm} 5\text{:}}\hspace{0.25cm} {\rm Inv_M}(e=4) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} e=4 \hspace{0.05cm}.$$
Für das Nullelement $d = 0$ existiert dagegen keine multiplikative Inverse.
(7) Bezüglich der primitiven Elemente erhält man
- $$a \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 3 \hspace{0.05cm},\hspace{0.2cm} a^2 = 9 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},\hspace{0.2cm} a^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} a^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm primitiv}\hspace{0.05cm},$$
- $$b \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \hspace{0.05cm},\hspace{0.2cm} b^2 = 4 \hspace{0.05cm},\hspace{0.2cm} b^3 = 8 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},\hspace{0.2cm} b^4 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm primitiv}\hspace{0.05cm},$$
- $$e \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 4 \hspace{0.05cm},\hspace{0.2cm} e^2 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},\hspace{0.2cm} e^3 = \hspace{0.05cm} ...\hspace{0.05cm}= 4\hspace{0.05cm},\hspace{0.2cm} e^4 =\hspace{0.05cm} ...\hspace{0.05cm} = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm nicht\hspace{0.15cm} primitiv}\hspace{0.05cm}.$$
Von der Menge $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\}$ sind "$2$" und "$3$" primitive Elemente ⇒ Lösungsvorschläge 1 und 2.