Exercise 1.09: BPSK and 4-QAM

Phase diagrams of BPSK and 4-QAM

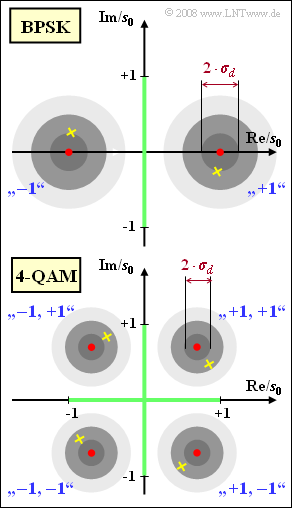
The diagram shows schematically the phase diagrams of the binary phase modulation (abbreviated BPSK) and the quadrature amplitude modulation (called 4–QAM).

The latter can be described by two BPSK systems with cosine and minus-sine carriers, where for each of the subcomponents the transmission amplitude is reduced by a factor of $\sqrt{2}$ compared to BPSK.
The envelope of the total signal $s(t)$ is thus also constant equal to $s_{0}$.
The error probability depending on the quotient $E_{\rm B}/N_{0}$ is the same for BPSK and 4–QAM:

$$p_{\rm B} = \ {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{E_{\rm B}/{ N_0 }} \right ).$$

However, the error probability of the BPSK system can also be expressed in the form

$$p_{\rm B,\hspace{0.04cm}BPSK} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{T_{\rm B}}}$$

Correspondingly, for the 4-QAM system:

$$p_{\rm B,\hspace{0.04cm}QAM} = {\rm Q}\left ( \frac{s_0/\sqrt{2}}{\sigma_d } \right )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}.$$

The equations are valid only under the condition of exact phase synchronization:

If there is a phase offset $\Delta\phi_{\rm T}$ between the transmitted and received carrier signals, the error probability increases significantly, with BPSK and QAM systems being degraded differently.
In the phase diagram, the phase offset is noticeable by a rotation of the point clouds. In the diagram, the centers of the point clouds for $\Delta\phi_{\rm T} = 15^\circ$ are marked by yellow crosses, while the red circles indicate the centers for $\Delta\phi_{\rm T} = 0$.

$E_{\rm B}/N_{0} = 8$ always holds, so the error probabilities of BPSK and QAM in the best case (without phase shift) are respectively as follows ⇒ Exercise 1.8Z:

$$p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$

Further remarks:

If we denote the distance of the BPSK useful samples from the (vertical) decision threshold by $s_{0}$, we get $\sigma_{d} = s_{0}/4$ for the noise rms value. The lighter circles in the diagram mark the contour lines with radius $2\cdot \sigma_{d}$ and $3\cdot \sigma_{d}$ of the Gaussian 2D PDF.

For the 4-QAM, compared to the BPSK, the distances of the useful samples drawn in red from the now two decision thresholds are each smaller by a factor of $\sqrt{2}$, but it also results in a noise rms value $\sigma_{d}$ smaller by the same factor.

Notes:

The exercise belongs to the chapter Linear Digital Modulation - Coherent Demodulation.
Reference is made in particular to the section Phase offset between transmitter and receiver.

You can determine the values of the Q function with the applet Complementary Gaussian Error Functions.

Questions

Solution

(1) Rotating the phase diagram by $\Delta\phi_{\rm T} = 15^\circ$ decreases the distance of the useful samples from the threshold by $\cos(15^\circ) \approx 0.966$. It follows that:

$$p_{\rm B} = {\rm Q}(0.966 \cdot 4) \approx {\rm Q}(3.86)= 0.57 \cdot 10^{-4}\hspace{0.1cm}\underline {= 0.0057\, \%}.$$

(2) Analogous to subtask (1), $\cos(45^\circ) \approx 0.707$ is obtained:

$$p_{\rm B} = {\rm Q}(0.707 \cdot 4) \approx {\rm Q}(2.83)\hspace{0.1cm}\underline {= 0.233 \, \%}.$$

(3) For 4-QAM, clockwise rotation by $\Delta\phi_{\rm T}$ increases the distance

from the horizontal threshold (decision of the first bit) equals $s_{0} \cdot \cos(45^\circ + \Delta\phi_{\rm T})$, i.e., smaller than without phase shift,
from the vertical threshold (decision of the second bit) equal to $s_{0} \cdot \cos(45^\circ - \Delta\phi_{\rm T})$, thus larger than without phase shift.

Thus, we obtain for the average error probability:

$$p_{\rm B} = {1}/{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ+{\rm \Delta} \phi_{\rm T}) \cdot s_0}{0.25 \cdot s_0 / \sqrt{2}} \right ) + {1}/{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ-{\rm \Delta} \phi_{\rm T}) \cdot s_0}{0.25 \cdot s_0 / \sqrt{2}}\right ).$$

This already takes into account the smaller noise rms value of the 4-QAM.
As a check, we calculate the error probability for $\Delta\phi_{\rm T} = 0$:

$$p_{\rm B} = {1}/{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ) \cdot 4}{1 / \sqrt{2}} \right ) +{1}/{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ) \cdot 4}{1 / \sqrt{2}} \right )= {\rm Q}(4) = 0.317 \cdot 10^{-4}.$$

On the other hand, we obtain with $\Delta\phi_{\rm T} = 15^\circ$:

$$p_{\rm B} = {1}/{2} \cdot {\rm Q}\left ( \frac{\cos(60^\circ) \cdot 4}{1 / \sqrt{2}} \right ) +{1}/{2} \cdot {\rm Q}\left ( \frac{\cos(30^\circ) \cdot 4}{1 / \sqrt{2}} \right )= {1}/{2} \cdot \left [{\rm Q}(2.83)+ {\rm Q}(4.90)\right]$$

$$\Rightarrow \hspace{0.3cm} p_{\rm B} \approx \frac{1}{2} \cdot \left [0.233 \cdot 10^{-2}+ 0.479 \cdot 10^{-6}\right] \hspace{0.1cm}\underline {= 0.117 \, \%}.$$

(4) With a phase shift of $45^\circ$, one obtains from the equation generally derived above:

$$p_{\rm B} ={1}/{2} \cdot {\rm Q}\left ( \frac{\cos(90^\circ) \cdot 4}{1 / \sqrt{2}} \right ) +{1}/{2} \cdot {\rm Q}\left ( \frac{\cos(0^\circ) \cdot 4}{1 / \sqrt{2}} \right )= {1}/{2} \cdot \left [{\rm Q}(0)+ {\rm Q}(5.66)\right] \approx 0.25\hspace{0.1cm}\underline {= 25 \, \%}.$$

That is:

The error rate for the first bit is $50\%$.
In contrast, the second bit is decided almost error-free $(\approx 10^{–8})$.
Overall, this results in a mean error probability of approx. $25\%$.