Difference between revisions of "Aufgaben:Exercise 1.17: About the Channel Coding Theorem"
From LNTwww
m (Text replacement - "„" to """) |
|||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding |
| Line 5: | Line 5: | ||
}} | }} | ||
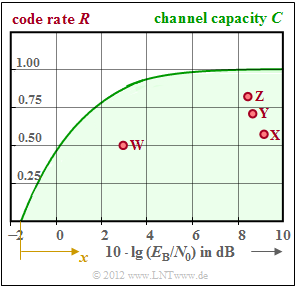
| − | [[File: | + | [[File:EN_KC_A_1_17.png|right|frame|Channel capacity $($green$)$ and code rates $($red dots$)$ of some established systems]] |
| − | + | The graph shows the maximum allowable code rate $R < C$ according to Shannon's [[Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding#Channel_coding_theorem_and_channel_capacity|"channel coding theorem"]]: | |
| − | * | + | *The green curve indicates the channel capacity $C$ for the AWGN channel assuming a binary input signal ("BPSK"). |
| − | *In | + | *In the [[Aufgaben:Exercise_1.17Z:_BPSK_Channel_Capacity|Exercise 1.17Z]] a simple approximation is given for this. With the second abscissa |
:$$x = \frac {1.6\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}$$ | :$$x = \frac {1.6\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}$$ | ||
| − | : | + | :results approximately: |
| − | :$$C \approx \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} \\ \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm | + | :$$C \approx \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} \\ \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for\hspace{0.15cm}} x > 0, \\ \\{\rm for\hspace{0.15cm}} x < 0. \end{array}$$ |
| − | * | + | *For $R < C$, a code can be found which leads to the error probability "zero" for infinitely long blocks $(n → ∞)$. |
| + | *What this code looks like is not determined by the channel coding theorem and does not matter for this exercise. | ||
| − | |||
| − | |||
| − | |||
| + | Drawn into the graph as dots are the characteristics of established coding systems: | ||
| + | *The dots $\rm X$, $\rm Y$, $\rm Z$ mark three Hamming codes of different code lengths, namely with $n = 7$, $n = 15$ and $n = 31$. | ||
| + | |||
| + | *The coding system $\rm W$ is characterized by the parameters $R = 0.5$ and $10 \ \cdot \lg {E_{\rm B}/N_0} = 3 {\rm dB}$ . | ||
| + | Hints: | ||
| + | *This exercise belongs to the topic of chapter [[Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding|"Information Theoretical Limits of Channel Coding"]]. | ||
| + | *The information theoretical limit "channel capacity" refers to the error probability $\rm BER =0$. | ||
| − | + | *The plotted points of real transmission systems, on the other hand, result under the assumption $\rm BER = 10^{-5}$. | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the points belong to which Hamming code? Note: The graph was created for $\rm BER = 10^{-5}$ . |
|type="[]"} | |type="[]"} | ||
| − | + $\rm X$ | + | + $\rm X$ denotes the $(7, 4, 3)$ Hamming code. |
| − | + $\rm Y$ | + | + $\rm Y$ denotes the $(15, 11, 3)$ Hamming code. |
| − | + $\rm Z$ | + | + $\rm Z$ denotes the $(31, 26, 3)$ Hamming code. |
| − | {In | + | {In what direction(s) will the points $\rm X$, $\rm Y$ and $\rm Z$ shift if the graph is to be created for $\rm BER = 10^{-10}$ ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - To the left, |
| − | + | + | + to the right, |
| − | - | + | - to the top. |
| − | { | + | {To what code rate $R_{\rm max}$ could you run a system with the same $E_{\rm B}/N_{0} = 3 \ {\rm dB}$ as system $\rm W$ ? |
|type="{}"} | |type="{}"} | ||
$R_{\rm max} \ = \ $ { 0.84 3% } | $R_{\rm max} \ = \ $ { 0.84 3% } | ||
| − | { | + | {By what factor $A > 1$ could the transmit power of system $\rm W$ be decreased according to the channel capacity curve with $ R = 0.5$ ? |
|type="{}"} | |type="{}"} | ||
$A \ = \ $ { 1.94 3% } | $A \ = \ $ { 1.94 3% } | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are <u>all proposed solutions</u>: |
| − | * | + | *From the graph you can already see that the rate of $\rm Z$ is greater than the rate of $\rm Y$ and the rate of $\rm Y$ is greater than the rate of $\rm X$. |
| − | * | + | |
| − | + | *The actual rates of these three systems are $R_{\rm X} = 4/7 = 0.571$, $R_{\rm Y} = 11/15 = 0.733$, and $R_{\rm Z} = 26/31 = 0.839$. | |
| + | *In addition, since the $(31, 26, 3)$ Hamming code ⇒ code $\rm Z$ has the largest code word length $n$, it requires $n$ despite a larger code rate $R$ for ${\rm BER} = 10^{-5}$ a smaller $E_{\rm B}/N_{0}$ than the other two Hamming codes. | ||
| − | '''(2)''' | + | |
| − | * | + | '''(2)''' Correct is <u>the answer 2</u>: |
| − | * | + | *For a smaller bit error rate, one always needs a larger $E_{\rm B}/N_{0}$. |
| + | |||
| + | *There is no vertical shift, because even with $\rm BER = 10^{-10}$ there is no change in the code rates. | ||
| − | '''(3)''' | + | '''(3)''' For the logarithmized AWGN parameter $10 · \lg {E_{\rm B}/N_0} = 3 \ {\rm dB}$, we obtain the auxiliary quantity $x = 1.6 + 3 = 4.6.$ This gives: |
:$$R_{\rm max} = C (x = 4.6)= 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} 4.6} \hspace{0.15cm} \underline{= 0.84} \hspace{0.05cm}.$$ | :$$R_{\rm max} = C (x = 4.6)= 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} 4.6} \hspace{0.15cm} \underline{= 0.84} \hspace{0.05cm}.$$ | ||
| Line 85: | Line 89: | ||
| − | '''(4)''' | + | '''(4)''' Now, according to the given equation: |
:$$1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x = \frac{-{\rm ln}(0.5)}{-0.4} = 1.73\hspace{0.3cm} | :$$1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x = \frac{-{\rm ln}(0.5)}{-0.4} = 1.73\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 1.73 - 1.6 = 0.13 \,{\rm dB}\hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 1.73 - 1.6 = 0.13 \,{\rm dB}\hspace{0.05cm}.$$ | ||
| − | $10 · \lg {E_{\rm B}/N_0}$ | + | * $10 · \lg {E_{\rm B}/N_0}$ could thus be decreased by $3 \ \rm dB - 0.13 \ dB = 2.87 \ dB$, i.e. by a factor $A = 10^{0.287}\hspace{0.15cm} \underline{= 1.94} \hspace{0.05cm}.$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Channel Coding: Exercises|^1.7 | + | [[Category:Channel Coding: Exercises|^1.7 Channel Capacity^]] |
Latest revision as of 16:48, 28 September 2022
The graph shows the maximum allowable code rate $R < C$ according to Shannon's "channel coding theorem":
- The green curve indicates the channel capacity $C$ for the AWGN channel assuming a binary input signal ("BPSK").
- In the Exercise 1.17Z a simple approximation is given for this. With the second abscissa
- $$x = \frac {1.6\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}$$
- results approximately:
- $$C \approx \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} \\ \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for\hspace{0.15cm}} x > 0, \\ \\{\rm for\hspace{0.15cm}} x < 0. \end{array}$$
- For $R < C$, a code can be found which leads to the error probability "zero" for infinitely long blocks $(n → ∞)$.
- What this code looks like is not determined by the channel coding theorem and does not matter for this exercise.
Drawn into the graph as dots are the characteristics of established coding systems:
- The dots $\rm X$, $\rm Y$, $\rm Z$ mark three Hamming codes of different code lengths, namely with $n = 7$, $n = 15$ and $n = 31$.
- The coding system $\rm W$ is characterized by the parameters $R = 0.5$ and $10 \ \cdot \lg {E_{\rm B}/N_0} = 3 {\rm dB}$ .
Hints:
- This exercise belongs to the topic of chapter "Information Theoretical Limits of Channel Coding".
- The information theoretical limit "channel capacity" refers to the error probability $\rm BER =0$.
- The plotted points of real transmission systems, on the other hand, result under the assumption $\rm BER = 10^{-5}$.
Questions
Solution
(1) Correct are all proposed solutions:
- From the graph you can already see that the rate of $\rm Z$ is greater than the rate of $\rm Y$ and the rate of $\rm Y$ is greater than the rate of $\rm X$.
- The actual rates of these three systems are $R_{\rm X} = 4/7 = 0.571$, $R_{\rm Y} = 11/15 = 0.733$, and $R_{\rm Z} = 26/31 = 0.839$.
- In addition, since the $(31, 26, 3)$ Hamming code ⇒ code $\rm Z$ has the largest code word length $n$, it requires $n$ despite a larger code rate $R$ for ${\rm BER} = 10^{-5}$ a smaller $E_{\rm B}/N_{0}$ than the other two Hamming codes.
(2) Correct is the answer 2:
- For a smaller bit error rate, one always needs a larger $E_{\rm B}/N_{0}$.
- There is no vertical shift, because even with $\rm BER = 10^{-10}$ there is no change in the code rates.
(3) For the logarithmized AWGN parameter $10 · \lg {E_{\rm B}/N_0} = 3 \ {\rm dB}$, we obtain the auxiliary quantity $x = 1.6 + 3 = 4.6.$ This gives:
- $$R_{\rm max} = C (x = 4.6)= 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} 4.6} \hspace{0.15cm} \underline{= 0.84} \hspace{0.05cm}.$$
(4) Now, according to the given equation:
- $$1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x = \frac{-{\rm ln}(0.5)}{-0.4} = 1.73\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 1.73 - 1.6 = 0.13 \,{\rm dB}\hspace{0.05cm}.$$
- $10 · \lg {E_{\rm B}/N_0}$ could thus be decreased by $3 \ \rm dB - 0.13 \ dB = 2.87 \ dB$, i.e. by a factor $A = 10^{0.287}\hspace{0.15cm} \underline{= 1.94} \hspace{0.05cm}.$