Difference between revisions of "Aufgaben:Exercise 1.3Z: Rayleigh Fading Revisited"
m (Text replacement - "„" to """) |
|||
| (24 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Probability_Density_of_Rayleigh_Fading}} |
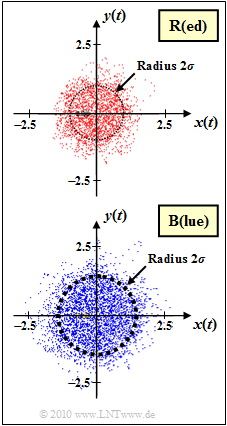
| − | [[File: | + | [[File:EN_Mob_A_1_3Z.png|right|frame|Two channels, characterized by complex factor $z(t)$]] |
| − | + | The graph shows the multiplicative factor $z(t) = x(t) + {\rm j} \cdot y(t)$ of two mobile radio channels (both without multipath propagation) in 2D–representation. The following is assumed: | |
| − | * | + | * The channel $\rm R$ $($the designation results from the color "Red" of the point cloud$)$ is Rayleigh distributed with $\sigma_{\rm R} = 0.5$. |
| − | * | + | * The probability density functions  $\rm (PDF)$ of the magnitude $a(t) = |z(t)|$ or the squared magnitude $p(t) = |z(t)|^2$ are $($with $\sigma = \sigma_{\rm R})$: |
:$$f_a(a) = | :$$f_a(a) = | ||
\left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \\ | \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm | + | \begin{array}{*{1}c} {\rm for}\hspace{0.15cm} a \ge 0 |
| − | \\ {\rm | + | \\ {\rm for}\hspace{0.15cm} a < 0 \\ \end{array} |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
:$$f_p(p) = | :$$f_p(p) = | ||
\left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^{ -{p}/(2\sigma^2)} \\ | \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^{ -{p}/(2\sigma^2)} \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm | + | \begin{array}{*{1}c} {\rm for}\hspace{0.15cm} p \ge 0 |
| − | \\ {\rm | + | \\ {\rm for}\hspace{0.15cm} p < 0 \\ \end{array} |
.$$ | .$$ | ||
| − | * | + | * For channel $\rm B$ ("Blue") only the point cloud is given.  It must be estimated whether Rayleigh fading is also present here, and if YES, how large the parameter $\sigma = \sigma_{\rm B}$ is for this channel. |
| − | * | + | * Finally, subtask '''(3)''' also refers to the PDF $f_{\it \phi}(\phi)$ of the phase function $\phi(t)$ , which is defined as follows: |
:$$\phi(t) = \arctan \hspace{0.15cm} \frac{y(t)}{x(t)} | :$$\phi(t) = \arctan \hspace{0.15cm} \frac{y(t)}{x(t)} | ||
| Line 28: | Line 28: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | * This task belongs to chapter [[Mobile_Communications/Probability_density_of_Rayleigh_fading|Probability density of Rayleigh fading]] of this book. |
| − | * | + | * A similar topic is treated with a different approach in chapter [[Theory_of_Stochastic_Signals/Further_distributions|Further distributions]] of the book "Stochastic Signal Theory". |
| − | * | + | * To check your results, you can use the interactive applet [[Applets:PDF,_CDF_and_Moments_of_Special_Distributions|PDF, CDF and Moments of Special Distributions]] of the book "Stochastic Signal Theory". |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Can the channel $\rm B$ also be modeled as Rayleigh fading? |
|type="()"} | |type="()"} | ||
| − | + | + | + Yes. |
| − | - | + | - No. |
| − | { | + | {Estimate the Rayleigh parameter of channel $\rm B$. Reminder: For channel $\rm R$ this parameter has the value $\sigma_{\rm R} = 0.5$. |
|type="{}"} | |type="{}"} | ||
$\sigma_{\rm B}\ = \ $ { 0.707 3% } | $\sigma_{\rm B}\ = \ $ { 0.707 3% } | ||
| − | { | + | {Are the probability density functions (PDFs) $f_{\it \phi}(\phi)$ of the phases different for channel $\rm R$ and $\rm B$ and if YES, how? |
|type="()"} | |type="()"} | ||
| − | - | + | - Yes. |
| − | + | + | + No. |
| − | { | + | {What is the PDF $f_a(a)$ with $a(t) = |z(t)|$ in both cases? |
|type="()"} | |type="()"} | ||
| − | - | + | - The random variable $a(t)$ is Gaussian distributed. |
| − | + | + | + The random variable $a(t)$ is Rayleigh distributed. |
| − | - | + | - The random variable $a(t)$ is positive and exponentially distributed. |
| − | { | + | {What is the PDF $f_p(p)$ in both cases with $p(t) = |z(t)|^2$? |
|type="()"} | |type="()"} | ||
| − | - | + | - The random variable $p(t)$ is Gaussian distributed. |
| − | - | + | - The random variable $p(t)$ is Rayleigh distributed. |
| − | + | + | + The random variable $p(t)$ is positive and exponentially distributed. |
| − | { | + | {What is the probability that the random variable $a(t) = |z(t)|$ is greater than a given value $A$? |
|type="()"} | |type="()"} | ||
| − | - | + | - ${\rm Pr}(|z(t)|) > A) = {\rm ln}(A/\sigma).$ |
| − | + | + | + ${\rm Pr}(|z(t)|) > A) = {\rm e}^{-A^2/2\sigma^2}.$ |
| − | - | + | - ${\rm Pr}(|z(t)|) > A) = {\rm e}^{-A/\sigma}.$ |
| − | { | + | {Calculate the probability ${\rm Pr}(|z(t)| > 1)$ for both channels. |
|type="{}"} | |type="{}"} | ||
| − | + | Channel $\rm R$:$\hspace{0.4cm} {\rm Pr}(|z(t)| > 1)\ = \ $ { 0.135 3% } | |
| − | + | Channel $\rm B$:$\hspace{0.4cm} {\rm Pr}(|z(t)| > 1)\ = \ $ { 0.368 3% } | |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u> | + | '''(1)''' <u>YES</u>: |
| − | * | + | *You can see the rotational symmetry here, too, if you consider that only $N = 10\hspace{0.05cm}000$ samples were displayed in the complex plane. |
| − | * | + | *Furthermore the following questions would not make sense if you answer "NO". |
| − | '''(2)''' | + | '''(2)''' By measuring the two drawn circles you can see that for the "blue" channel the scattering of real– and imaginary part are larger by a factor of about $1.4$ <br>$($exactly: $\sqrt{2})$ than for the "red" channel: |
| − | + | $$\sigma_{\rm B} = \sigma_{\rm R} \cdot \sqrt{2} = 0.5 \cdot \sqrt{2}= {1}/{\sqrt{2}}\hspace{0.15cm} \underline{\approx 0.707} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(3)''' <u> | + | '''(3)''' <u>NO</u>: |
| − | *In | + | *In both cases $f_{\it \phi}(\phi)$ describes a uniform distribution between $-\pi$ and $+\pi$. |
| − | * | + | *The larger amplitudes of channel $\rm B$ are not important for the phase function $\phi(t)$. |
| − | '''(4)''' | + | '''(4)''' <u>Solution 2</u> is correct: |
| − | * | + | *With Rayleigh fading, the real part $x(t)$ and the imaginary part $y(t)$ are each Gaussian distributed. |
| − | * | + | *The exponential distribution results for the square of the absolute value $p(t) = |z(t)|^2$. |
| − | '''(5)''' | + | '''(5)''' <u>Solution 3</u> is correct, as already explained in the sample solution for '''(4)'''. |
| − | '''(6)''' | + | '''(6)''' The magnitude $a(t)$ is Rayleigh distributed. Therefore, the following holds for the desired probability: |
:$${\rm Pr}(a > A) = \int_{A}^{\infty}\frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \hspace{0.15cm}{\rm d}a \hspace{0.05cm}.$$ | :$${\rm Pr}(a > A) = \int_{A}^{\infty}\frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \hspace{0.15cm}{\rm d}a \hspace{0.05cm}.$$ | ||
| − | *In | + | *In some formula collections you can find the solution for this integral, but not in all. |
| − | * | + | *But it is also valid with the one-sided exponentially distributed random variable $p = a^2$: |
| − | :$${\rm Pr}(a > A) = {\rm Pr}(p > A^2) = \frac{1}{2\sigma^2} \cdot\int_{A^2}^{\infty} | + | :$${\rm Pr}(a > A) = {\rm Pr}(p > A^2) = \frac{1}{2\sigma^2} \cdot\int_{A^2}^{\infty} {\rm e}^{ -{p}/(2\sigma^2)} \hspace{0.15cm}{\rm d}p \hspace{0.05cm}.$$ |
| − | * | + | *This integral is elementary and gives the result: |
| − | :$${\rm Pr}(a > A) = | + | :$${\rm Pr}(a > A) = {\rm e}^{ -{A^2}/(2\sigma^2)} \hspace{0.05cm}.$$ |
| − | + | The correct answer is therefore <u>solution 2</u>. | |
| − | '''(7)''' | + | '''(7)''' For the channel $\rm R$ and $\sigma = 0.5$ ⇒ $\sigma^2 = 0.25$, we have |
| − | :$${\rm Pr}(|z(t)| > 1) = | + | :$${\rm Pr}(|z(t)| > 1) = {\rm e}^{-2} \hspace{0.15cm} \underline{\approx 0.135} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *In | + | *In the upper graph this corresponds to the number of all points outside the circle drawn, based on the number $N = 10,000$ of all points. |
| − | * | + | *For the channel $\rm B$ because of the double variance $\sigma^2 = 0.5$, we have ${\rm Pr}(|z(t)|>1) = {\rm e}^{-1} \ \underline {\approx \ 0.368}$. |
| − | * | + | *The (not drawn) reference circle would also have radius $1$ in the bottom graph. |
| − | * | + | *The circle drawn in the bottom graph has a larger radius than $A = 1$, namely $A = \sqrt{2}\approx 1.414$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^1.2 PDF of Rayleigh Fading^]] |
Latest revision as of 16:43, 28 May 2021
The graph shows the multiplicative factor $z(t) = x(t) + {\rm j} \cdot y(t)$ of two mobile radio channels (both without multipath propagation) in 2D–representation. The following is assumed:
- The channel $\rm R$ $($the designation results from the color "Red" of the point cloud$)$ is Rayleigh distributed with $\sigma_{\rm R} = 0.5$.
- The probability density functions  $\rm (PDF)$ of the magnitude $a(t) = |z(t)|$ or the squared magnitude $p(t) = |z(t)|^2$ are $($with $\sigma = \sigma_{\rm R})$:
- $$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for}\hspace{0.15cm} a \ge 0 \\ {\rm for}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm},$$
- $$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^{ -{p}/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for}\hspace{0.15cm} p \ge 0 \\ {\rm for}\hspace{0.15cm} p < 0 \\ \end{array} .$$
- For channel $\rm B$ ("Blue") only the point cloud is given.  It must be estimated whether Rayleigh fading is also present here, and if YES, how large the parameter $\sigma = \sigma_{\rm B}$ is for this channel.
- Finally, subtask (3) also refers to the PDF $f_{\it \phi}(\phi)$ of the phase function $\phi(t)$ , which is defined as follows:
- $$\phi(t) = \arctan \hspace{0.15cm} \frac{y(t)}{x(t)} \hspace{0.05cm}.$$
Notes:
- This task belongs to chapter Probability density of Rayleigh fading of this book.
- A similar topic is treated with a different approach in chapter Further distributions of the book "Stochastic Signal Theory".
- To check your results, you can use the interactive applet PDF, CDF and Moments of Special Distributions of the book "Stochastic Signal Theory".
Questions
Solution
- You can see the rotational symmetry here, too, if you consider that only $N = 10\hspace{0.05cm}000$ samples were displayed in the complex plane.
- Furthermore the following questions would not make sense if you answer "NO".
(2) By measuring the two drawn circles you can see that for the "blue" channel the scattering of real– and imaginary part are larger by a factor of about $1.4$
$($exactly: $\sqrt{2})$ than for the "red" channel:
$$\sigma_{\rm B} = \sigma_{\rm R} \cdot \sqrt{2} = 0.5 \cdot \sqrt{2}= {1}/{\sqrt{2}}\hspace{0.15cm} \underline{\approx 0.707}
\hspace{0.05cm}.$$
(3) NO:
- In both cases $f_{\it \phi}(\phi)$ describes a uniform distribution between $-\pi$ and $+\pi$.
- The larger amplitudes of channel $\rm B$ are not important for the phase function $\phi(t)$.
(4) Solution 2 is correct:
- With Rayleigh fading, the real part $x(t)$ and the imaginary part $y(t)$ are each Gaussian distributed.
- The exponential distribution results for the square of the absolute value $p(t) = |z(t)|^2$.
(5) Solution 3 is correct, as already explained in the sample solution for (4).
(6) The magnitude $a(t)$ is Rayleigh distributed. Therefore, the following holds for the desired probability:
- $${\rm Pr}(a > A) = \int_{A}^{\infty}\frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \hspace{0.15cm}{\rm d}a \hspace{0.05cm}.$$
- In some formula collections you can find the solution for this integral, but not in all.
- But it is also valid with the one-sided exponentially distributed random variable $p = a^2$:
- $${\rm Pr}(a > A) = {\rm Pr}(p > A^2) = \frac{1}{2\sigma^2} \cdot\int_{A^2}^{\infty} {\rm e}^{ -{p}/(2\sigma^2)} \hspace{0.15cm}{\rm d}p \hspace{0.05cm}.$$
- This integral is elementary and gives the result:
- $${\rm Pr}(a > A) = {\rm e}^{ -{A^2}/(2\sigma^2)} \hspace{0.05cm}.$$
The correct answer is therefore solution 2.
(7) For the channel $\rm R$ and $\sigma = 0.5$ ⇒ $\sigma^2 = 0.25$, we have
- $${\rm Pr}(|z(t)| > 1) = {\rm e}^{-2} \hspace{0.15cm} \underline{\approx 0.135} \hspace{0.05cm}.$$
- In the upper graph this corresponds to the number of all points outside the circle drawn, based on the number $N = 10,000$ of all points.
- For the channel $\rm B$ because of the double variance $\sigma^2 = 0.5$, we have ${\rm Pr}(|z(t)|>1) = {\rm e}^{-1} \ \underline {\approx \ 0.368}$.
- The (not drawn) reference circle would also have radius $1$ in the bottom graph.
- The circle drawn in the bottom graph has a larger radius than $A = 1$, namely $A = \sqrt{2}\approx 1.414$.