Difference between revisions of "Aufgaben:Exercise 1.7: Coding for Broadband ISDN"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/Further_Developments_of_ISDN |
}} | }} | ||
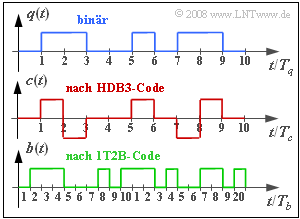
| − | [[File:EN_Bei_A_1_7.png|right|frame|HDB3 | + | [[File:EN_Bei_A_1_7.png|right|frame|HDB3 and 1T2B coding]] |
| − | + | For conventional ISDN over copper lines the HDB3 code is used – see [[Aufgaben:Exercise_1.5:_HDB3_Coding|"Exercise 1.5"]]: | |
| − | + | This was derived from the so-called AMI code, | |
| − | * | + | *is like the latter a pseudo-ternary code, |
| − | * | + | *but avoids more than three consecutive "$0$" symbols, |
| − | * | + | *by deliberately violating the stricter AMI coding rule for longer zero sequences. |
| − | + | The graph shows the HDB3 encoded signal $c(t)$ resulting from the binary redundancy-free source signal $q(t)$. Since there are no more than three consecutive zeros in the source signal, $c(t)$ is identical to the AMI-encoded signal. | |
| − | + | The broadband ISDN planned for the late 1990s was to provide data rates of up to 155 Mbit/s compared with 144 kbit/s of conventional ISDN with two B channels and one D channel. To achieve this higher data rate, it was necessary to | |
| − | * | + | *newer technology (ATM) had to be used, |
| − | * | + | *secondly, the transmission medium had to be changed from copper to fiber optics. |
| − | + | However, since the HDB3-encoded signal $c(t) ∈ \{–1, \ 0, +1\}$ cannot be transmitted by means of light, a second encoding was required. The '''1T2B code''' provided for this purpose replaces each ternary symbol with two binary symbols. The diagram below shows an example of the binary signal $b(t) ∈ \{0, 1\}$, which results from the signal $c(t)$ after this 1T2B coding. | |
| − | + | For this exercise, assume that the bit rate of the redundancy-free source signal $q(t)$ is equal to $R_{q} = 2.048 \ \rm Mbit/s$. The respective symbol durations of the signals $q(t), c(t)$ and $b(t)$ are denoted by $T_{q}$, $T_{c}$ and $T_{b}$. | |
| − | + | The equivalent bit rate of the pseudo-ternary signal $c(t)$ is $R_{c} = {\rm log_2}(3)/T_{c}$, from which the bit rate $R_{q} = 1/T_{q}$ of the source signal can be used to calculate the relative redundancy of the AMI or HDB3 code: | |
:$$r_{\rm HDB3} = \frac{R_c - R_q}{R_c}= 1 - \frac{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_c)} \hspace{0.05cm}.$$ | :$$r_{\rm HDB3} = \frac{R_c - R_q}{R_c}= 1 - \frac{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_c)} \hspace{0.05cm}.$$ | ||
| − | + | A similar equation can be established for the 1T2B code, as well as for the two codes in combination. | |
| Line 34: | Line 34: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The exercise belongs to the chapter [[Examples_of_Communication_Systems/Further_Developments_of_ISDN|"Further Developments of ISDN"]]. |
| − | * | + | * Redundancy is defined and illustrated with examples in the chapter [[Digital_Signal_Transmission/Basics_of_Coded_Transmission|"Basics of Coded Transmission"]] of the book "Digital Signal Transmission". |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the assignment of the '''1T2B''' code? |
|type="()"} | |type="()"} | ||
- $c(t) = +1 \Rightarrow b(t) = 10, \hspace{1cm}c(t) = 0 \Rightarrow b(t) = 00, \hspace{1cm}c(t) = -1 \Rightarrow b(t) = 01,$ | - $c(t) = +1 \Rightarrow b(t) = 10, \hspace{1cm}c(t) = 0 \Rightarrow b(t) = 00, \hspace{1cm}c(t) = -1 \Rightarrow b(t) = 01,$ | ||
| Line 50: | Line 50: | ||
- $c(t) = +1 \Rightarrow b(t) = 01, \hspace{1cm}c(t) = 0 \Rightarrow b(t) = 11, \hspace{1cm}c(t) = -1 \Rightarrow b(t) = 10.$ | - $c(t) = +1 \Rightarrow b(t) = 01, \hspace{1cm}c(t) = 0 \Rightarrow b(t) = 11, \hspace{1cm}c(t) = -1 \Rightarrow b(t) = 10.$ | ||
| − | { | + | {What are the symbol durations of $q(t), c(t)$ and $b(t)$? |
|type="{}"} | |type="{}"} | ||
$T_{q} \ = \ $ { 0.488 3% } $\ \rm µ s$ | $T_{q} \ = \ $ { 0.488 3% } $\ \rm µ s$ | ||
| Line 56: | Line 56: | ||
$T_{b} \ = \ $ { 0.244 3% } $\ \rm µ s$ | $T_{b} \ = \ $ { 0.244 3% } $\ \rm µ s$ | ||
| − | { | + | {Calculate the relative redundancy of the '''HDB3''' code. |
|type="{}"} | |type="{}"} | ||
$r_{\rm HDB3} \ = \ $ { 36.9 3% } $\ \%$ | $r_{\rm HDB3} \ = \ $ { 36.9 3% } $\ \%$ | ||
| − | { | + | {Calculate the relative redundancy of the '''1T2B''' code. |
|type="{}"} | |type="{}"} | ||
$r_{\rm 1T2B} \ = \ $ { 20.7 3% } $\ \%$ | $r_{\rm 1T2B} \ = \ $ { 20.7 3% } $\ \%$ | ||
| − | { | + | {What is the relative redundancy of the signal $b(t)$, i.e. the '''combination''' of HDB3 code and 1T2B code? |
|type="{}"} | |type="{}"} | ||
$r_{\rm HDB3+1T2B} \ = \ $ { 50 3% } $\ \%$ | $r_{\rm HDB3+1T2B} \ = \ $ { 50 3% } $\ \%$ | ||
| Line 70: | Line 70: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Solution 2</u> is correct, as a comparison of the signal characteristics $c(t)$ and $b(t)$ shows. |
| − | '''(2)''' | + | '''(2)''' The symbol duration (bit duration) of $q(t)$ is $T_{q} \hspace{0.15cm}\underline{ = 1/R_{q} = 0.488 \ \rm µ s}$. |
| − | * | + | *The symbol duration of the AMI code (and the HDB3 code) is exactly the same: $T_{c} \hspace{0.15cm}\underline{ = 0.488 \ \rm µ s}$. |
| − | * | + | *In contrast, the symbol duration (bit duration) after 1T2B encoding is only half as large: $T_{b} = T_{c}/2 \hspace{0.15cm}\underline{= 0.244 \ \rm µ s}$. |
| − | '''(3)''' | + | '''(3)''' Using the given equation, with $M_{q} = 2, M_{c} = 3$ and $T_{c} = T_{q}$, we get: |
:$$r_{\rm HDB3} = 1 - \frac{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_c)} = 1 - \frac{1}{{\rm log_2}\hspace{0.1cm}(3)} \hspace{0.15cm}\underline{= 36.9\,\%} \hspace{0.05cm}.$$ | :$$r_{\rm HDB3} = 1 - \frac{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_c)} = 1 - \frac{1}{{\rm log_2}\hspace{0.1cm}(3)} \hspace{0.15cm}\underline{= 36.9\,\%} \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' Fitting the equation to the 1T2B code, we obtain with $M_{c} = 3, M_{b} = 2, T_{b} = T_{c}/2$: |
:$$r_{\rm 1T2B} = 1 - \frac{T_b \cdot {\rm log_2}\hspace{0.1cm}(M_c)}{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_b)} = 1 - \frac{{\rm log_2}\hspace{0.1cm}(3)}{2} \hspace{0.15cm}\underline{= 20.7\,\%} \hspace{0.05cm}.$$ | :$$r_{\rm 1T2B} = 1 - \frac{T_b \cdot {\rm log_2}\hspace{0.1cm}(M_c)}{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_b)} = 1 - \frac{{\rm log_2}\hspace{0.1cm}(3)}{2} \hspace{0.15cm}\underline{= 20.7\,\%} \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' The resulting redundancy of both codes is obtained by relating the given equation to the input signal $q(t)$ and the output signal $c(t)$. With $M_{q} = M_{b} = 2$ and $T_{b} = T_{q}/2$ it follows: |
:$$r_{\rm HDB3+1T2B} = 1 - \frac{T_b \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_b)} = 1 - \frac{T_b}{T_q} \hspace{0.15cm}\underline{= 50\,\%} \hspace{0.05cm}.$$ | :$$r_{\rm HDB3+1T2B} = 1 - \frac{T_b \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_b)} = 1 - \frac{T_b}{T_q} \hspace{0.15cm}\underline{= 50\,\%} \hspace{0.05cm}.$$ | ||
| − | + | The same result is obtained by the calculation | |
:$$1-r_{\rm HDB3+1T2B} \ = \ (1-r_{\rm HDB3}) \cdot (1-r_{\rm 1T2B}) =(1- 1 +\frac{1}{{\rm log_2}\hspace{0.1cm}(3)}) \cdot (1-1+ \frac{{\rm log_2}\hspace{0.1cm}(3)}{2}) = 50\,\% \hspace{0.05cm}.$$ | :$$1-r_{\rm HDB3+1T2B} \ = \ (1-r_{\rm HDB3}) \cdot (1-r_{\rm 1T2B}) =(1- 1 +\frac{1}{{\rm log_2}\hspace{0.1cm}(3)}) \cdot (1-1+ \frac{{\rm log_2}\hspace{0.1cm}(3)}{2}) = 50\,\% \hspace{0.05cm}.$$ | ||
:$$\Rightarrow \hspace{0.3cm}r_{\rm HDB3+1T2B}= 50\,\% \hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm}r_{\rm HDB3+1T2B}= 50\,\% \hspace{0.05cm}.$$ | ||
Revision as of 18:33, 30 October 2022
For conventional ISDN over copper lines the HDB3 code is used – see "Exercise 1.5":
This was derived from the so-called AMI code,
- is like the latter a pseudo-ternary code,
- but avoids more than three consecutive "$0$" symbols,
- by deliberately violating the stricter AMI coding rule for longer zero sequences.
The graph shows the HDB3 encoded signal $c(t)$ resulting from the binary redundancy-free source signal $q(t)$. Since there are no more than three consecutive zeros in the source signal, $c(t)$ is identical to the AMI-encoded signal.
The broadband ISDN planned for the late 1990s was to provide data rates of up to 155 Mbit/s compared with 144 kbit/s of conventional ISDN with two B channels and one D channel. To achieve this higher data rate, it was necessary to
- newer technology (ATM) had to be used,
- secondly, the transmission medium had to be changed from copper to fiber optics.
However, since the HDB3-encoded signal $c(t) ∈ \{–1, \ 0, +1\}$ cannot be transmitted by means of light, a second encoding was required. The 1T2B code provided for this purpose replaces each ternary symbol with two binary symbols. The diagram below shows an example of the binary signal $b(t) ∈ \{0, 1\}$, which results from the signal $c(t)$ after this 1T2B coding.
For this exercise, assume that the bit rate of the redundancy-free source signal $q(t)$ is equal to $R_{q} = 2.048 \ \rm Mbit/s$. The respective symbol durations of the signals $q(t), c(t)$ and $b(t)$ are denoted by $T_{q}$, $T_{c}$ and $T_{b}$.
The equivalent bit rate of the pseudo-ternary signal $c(t)$ is $R_{c} = {\rm log_2}(3)/T_{c}$, from which the bit rate $R_{q} = 1/T_{q}$ of the source signal can be used to calculate the relative redundancy of the AMI or HDB3 code:
- $$r_{\rm HDB3} = \frac{R_c - R_q}{R_c}= 1 - \frac{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_c)} \hspace{0.05cm}.$$
A similar equation can be established for the 1T2B code, as well as for the two codes in combination.
Notes:
- The exercise belongs to the chapter "Further Developments of ISDN".
- Redundancy is defined and illustrated with examples in the chapter "Basics of Coded Transmission" of the book "Digital Signal Transmission".
Questions
Solution
(1) Solution 2 is correct, as a comparison of the signal characteristics $c(t)$ and $b(t)$ shows.
(2) The symbol duration (bit duration) of $q(t)$ is $T_{q} \hspace{0.15cm}\underline{ = 1/R_{q} = 0.488 \ \rm µ s}$.
- The symbol duration of the AMI code (and the HDB3 code) is exactly the same: $T_{c} \hspace{0.15cm}\underline{ = 0.488 \ \rm µ s}$.
- In contrast, the symbol duration (bit duration) after 1T2B encoding is only half as large: $T_{b} = T_{c}/2 \hspace{0.15cm}\underline{= 0.244 \ \rm µ s}$.
(3) Using the given equation, with $M_{q} = 2, M_{c} = 3$ and $T_{c} = T_{q}$, we get:
- $$r_{\rm HDB3} = 1 - \frac{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_c)} = 1 - \frac{1}{{\rm log_2}\hspace{0.1cm}(3)} \hspace{0.15cm}\underline{= 36.9\,\%} \hspace{0.05cm}.$$
(4) Fitting the equation to the 1T2B code, we obtain with $M_{c} = 3, M_{b} = 2, T_{b} = T_{c}/2$:
- $$r_{\rm 1T2B} = 1 - \frac{T_b \cdot {\rm log_2}\hspace{0.1cm}(M_c)}{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_b)} = 1 - \frac{{\rm log_2}\hspace{0.1cm}(3)}{2} \hspace{0.15cm}\underline{= 20.7\,\%} \hspace{0.05cm}.$$
(5) The resulting redundancy of both codes is obtained by relating the given equation to the input signal $q(t)$ and the output signal $c(t)$. With $M_{q} = M_{b} = 2$ and $T_{b} = T_{q}/2$ it follows:
- $$r_{\rm HDB3+1T2B} = 1 - \frac{T_b \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_b)} = 1 - \frac{T_b}{T_q} \hspace{0.15cm}\underline{= 50\,\%} \hspace{0.05cm}.$$
The same result is obtained by the calculation
- $$1-r_{\rm HDB3+1T2B} \ = \ (1-r_{\rm HDB3}) \cdot (1-r_{\rm 1T2B}) =(1- 1 +\frac{1}{{\rm log_2}\hspace{0.1cm}(3)}) \cdot (1-1+ \frac{{\rm log_2}\hspace{0.1cm}(3)}{2}) = 50\,\% \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm}r_{\rm HDB3+1T2B}= 50\,\% \hspace{0.05cm}.$$