Difference between revisions of "Aufgaben:Exercise 1.7: Nearly Causal Gaussian Low-Pass Filter"
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory}} |
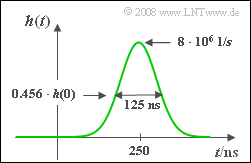
| − | [[File:P_ID863__LZI_A_1_7.png|right|frame| | + | [[File:P_ID863__LZI_A_1_7.png|right|frame|Impulse response of a nearly causal Gaussian lowp-ass filter]] |
| − | + | Measurements have shown that an LTI–system can be well approximated by a Gaussian low-pass filter if an additional runtime $τ$ is taken into account. Thus, the frequency response is: | |
:$$H(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f)^2} \cdot {\rm e}^{-{\rm | :$$H(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f)^2} \cdot {\rm e}^{-{\rm | ||
j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \tau}.$$ | j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \tau}.$$ | ||
| − | + | The two system parameters, | |
| − | * | + | *the equivalent duration of the impulse $Δt = 1/Δf$ and |
| − | * | + | *the delay time $τ$, |
| − | + | can be taken from the impulse response $h(t)$ shown in the graph. | |
| − | * | + | *It is obvious that this model does not correspond exactly to the (causal) reality since the impulse response $h(t)$ does not completely vanish even for $t < 0$ . |
| − | * | + | *Therefore, in subtask '''(3)''' the maximum relative error is aked for and defined as follows: |
:$$\varepsilon_{\rm max} = \frac{\max_{t \hspace{0.02cm}< | :$$\varepsilon_{\rm max} = \frac{\max_{t \hspace{0.02cm}< | ||
\hspace{0.1cm}0}|h(t)|}{h(t = \tau)}.$$ | \hspace{0.1cm}0}|h(t)|}{h(t = \tau)}.$$ | ||
| − | In | + | In words: The maximum relative error $ε_{\rm max}$ is equal to the maximum value of the impulse response $h(t)$ at negative times with respect to the maximum value $h(t = τ)$ of the impulse response. |
| Line 24: | Line 24: | ||
| − | + | ''Please note:'' | |
| − | '' | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory|Some Low-Pass Functions in Systems Theory]]. |
| − | * | + | *In particular, reference is made to the page [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Gaussian_low-pass_filter|Gaussian low-pass filter]]. |
| − | + | *You can use the Gaussian (error) integral to calculate step and rectangle responses: | |
| − | * | ||
| − | * | ||
:$${\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot | :$${\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot | ||
\int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$ | \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$ | ||
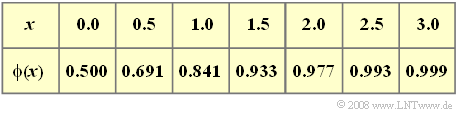
| − | [[File:P_ID864__LZI_A_1_7b.png |center|frame| | + | [[File:P_ID864__LZI_A_1_7b.png |center|frame|Some values of the Gaussian error function]] |
| Line 39: | Line 37: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the equivalent bandwidth $\Delta f $ and the runtime $\tau $? |
|type="{}"} | |type="{}"} | ||
$\Delta f \ = \ $ { 8 3% } $\ \rm MHz$ | $\Delta f \ = \ $ { 8 3% } $\ \rm MHz$ | ||
| Line 48: | Line 46: | ||
| − | { | + | {It holds that $x(t) = 1 \hspace{0.05cm}{\rm V} · \cos(2π · 6\ {\rm MHz }· t)$. What is the output signal $y(t)$? What is the signal value at time $t = 0$? |
|type="{}"} | |type="{}"} | ||
$y(t = 0) \ = \ $ { -0.175--0.165 } $\ \rm V$ | $y(t = 0) \ = \ $ { -0.175--0.165 } $\ \rm V$ | ||
| − | { | + | {Actually, $h(t < 0) = 0$ should hold due to causality. What is the maximum relative error $\varepsilon_{\rm max}$ of the model under consideration? <br>See the definition of $\varepsilon_{\rm max}$ on the information page. |
|type="{}"} | |type="{}"} | ||
$\varepsilon_{\rm max} \ = \ $ { 3.49 5% } $\ \cdot 10^{-6}$ | $\varepsilon_{\rm max} \ = \ $ { 3.49 5% } $\ \cdot 10^{-6}$ | ||
| − | { | + | {Compute the (dimensionless) step response $σ(t)$. What values arise as a result at times $t = 250 \hspace{0.05cm} \rm ns$ and $t = 300 \hspace{0.05cm} \rm ns$? |
|type="{}"} | |type="{}"} | ||
$σ(t = 250\hspace{0.05cm} \rm ns)\ = \ $ { 0.5 5% } | $σ(t = 250\hspace{0.05cm} \rm ns)\ = \ $ { 0.5 5% } | ||
| Line 65: | Line 63: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The equivalent bandwidth $Δf$ is equal to $h(t = τ) \hspace{0.05cm} \rm \underline{= \ 8 \ MHz}$. |
| − | * | + | *This is also the reciprocal of the equivalent impulse duration $Δt = 125 \ \rm ns$. |
| − | * | + | *The phase runtime $τ \hspace{0.15cm} \rm \underline{= \ 250 \ \rm ns}$ can be read directly from the graph, too. |
| − | '''(2)''' | + | '''(2)''' Without consideration of the runtime the result would be a cosine signal with the amplitude |
:$$A_y = 1\,{\rm V} \cdot {\rm e}^{-\pi({ {6\,\rm MHz} }/{ {8\,\rm MHz} })^2}= 0.171\,{\rm V}.$$ | :$$A_y = 1\,{\rm V} \cdot {\rm e}^{-\pi({ {6\,\rm MHz} }/{ {8\,\rm MHz} })^2}= 0.171\,{\rm V}.$$ | ||
| − | * | + | *The runtime causes a phase shift of $3π$: |
:$$ y(t) = A_y \cdot {\rm cos}(2\pi f_0 ( t - \tau) ) = A_y \cdot {\rm cos}(2\pi f_0 t - 2\pi \cdot {6\,\rm MHz}\cdot {250\,\rm ns} ) = A_y \cdot {\rm cos}(2\pi f_0 t - 3\pi ) = -A_y \cdot {\rm cos}(2\pi f_0 t ).$$ | :$$ y(t) = A_y \cdot {\rm cos}(2\pi f_0 ( t - \tau) ) = A_y \cdot {\rm cos}(2\pi f_0 t - 2\pi \cdot {6\,\rm MHz}\cdot {250\,\rm ns} ) = A_y \cdot {\rm cos}(2\pi f_0 t - 3\pi ) = -A_y \cdot {\rm cos}(2\pi f_0 t ).$$ | ||
| − | * | + | *Hence, the searched-for value is $y(t = 0) \hspace{0.05cm} \rm \underline{= \ –0.171 \ V}$. |
| − | '''(3)''' | + | '''(3)''' The impulse response is: |
:$$h(t) = h_{\rm GTP}(t - \tau) =\Delta f \cdot {\rm e}^{-\pi(\frac{t - \tau}{\Delta t})^2} .$$ | :$$h(t) = h_{\rm GTP}(t - \tau) =\Delta f \cdot {\rm e}^{-\pi(\frac{t - \tau}{\Delta t})^2} .$$ | ||
| − | * | + | *Since $h(t)$ increases steadily in the range $t < 0$ the maximum value (at negative times) occurs approximately at $t = 0$ : |
:$$h(t = 0) = \Delta f \cdot {\rm e}^{-\pi(\frac{ \tau}{\Delta t})^2}= \Delta f \cdot {\rm e}^{-4\pi} .$$ | :$$h(t = 0) = \Delta f \cdot {\rm e}^{-\pi(\frac{ \tau}{\Delta t})^2}= \Delta f \cdot {\rm e}^{-4\pi} .$$ | ||
| − | * | + | *Using $h(t = τ) = Δf$ the following is obtained: |
:$$\varepsilon_{\rm max}= {\rm e}^{-4\pi}\hspace{0.15cm}\underline{ \approx 3.49} \cdot 10^{-6} .$$ | :$$\varepsilon_{\rm max}= {\rm e}^{-4\pi}\hspace{0.15cm}\underline{ \approx 3.49} \cdot 10^{-6} .$$ | ||
| − | '''(4)''' | + | '''(4)''' For the moment, we leave the phase runtime $τ$ of the second system out of consideration and compute the step response of the Gaussian low-pass filter: |
:$$\sigma_{\rm GTP}(t) = \frac{1}{\Delta t} \cdot \int_{ -\infty }^{ t } {{\rm e}^{-\pi \left({t\hspace{0.05cm}'}/{\Delta t}\right)^2}} \hspace{0.1cm}{\rm d}t'.$$ | :$$\sigma_{\rm GTP}(t) = \frac{1}{\Delta t} \cdot \int_{ -\infty }^{ t } {{\rm e}^{-\pi \left({t\hspace{0.05cm}'}/{\Delta t}\right)^2}} \hspace{0.1cm}{\rm d}t'.$$ | ||
| − | * | + | *After the substitution $u = t\hspace{0.05cm}' \cdot {\sqrt{2\pi}}/{\Delta t}$ the following arises as a result with the Gaussian (error) integral $ϕ(x)$: |
:$$\sigma_{\rm GTP}(t) = \frac{1}{\sqrt{2 \pi } } \cdot \int_{ -\infty }^{ \sqrt{2\pi}\cdot\hspace{0.05cm} t / \Delta t } { {\rm e}^{-u^2/2} } \hspace{0.1cm}{\rm d}u = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t}{\Delta t }),\hspace{1cm} | :$$\sigma_{\rm GTP}(t) = \frac{1}{\sqrt{2 \pi } } \cdot \int_{ -\infty }^{ \sqrt{2\pi}\cdot\hspace{0.05cm} t / \Delta t } { {\rm e}^{-u^2/2} } \hspace{0.1cm}{\rm d}u = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t}{\Delta t }),\hspace{1cm} | ||
{\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot | {\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot | ||
\int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$ | \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$ | ||
| − | * | + | *Taking into account the runtime $τ$ one thus obtains for the total step response: |
:$$\sigma(t) = \sigma_{\rm GTP}(t - \tau) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t - \tau}{\Delta t }).$$ | :$$\sigma(t) = \sigma_{\rm GTP}(t - \tau) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t - \tau}{\Delta t }).$$ | ||
| − | * | + | *The value at $t = τ = 250 \ \rm ns$ is |
:$$\sigma(t = {250\,\rm ns}) = \sigma_{\rm GTP}(t = 0) =\ \rm \underline{ϕ(0) \ = \ 0.500}.$$ | :$$\sigma(t = {250\,\rm ns}) = \sigma_{\rm GTP}(t = 0) =\ \rm \underline{ϕ(0) \ = \ 0.500}.$$ | ||
| − | * | + | *Accordingly, for $t = τ = 300 \ \rm ns$ the following is obtained: |
:$$\sigma(t = {300\,\rm ns}) = \sigma_{\rm GTP}(t = {50\,\rm ns}) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{ {50\,\rm ns} }{ {125\,\rm ns} })\approx {\rm \phi}(1)\hspace{0.15cm}\underline{ = 0.841}.$$ | :$$\sigma(t = {300\,\rm ns}) = \sigma_{\rm GTP}(t = {50\,\rm ns}) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{ {50\,\rm ns} }{ {125\,\rm ns} })\approx {\rm \phi}(1)\hspace{0.15cm}\underline{ = 0.841}.$$ | ||
Latest revision as of 14:49, 8 September 2021
Measurements have shown that an LTI–system can be well approximated by a Gaussian low-pass filter if an additional runtime $τ$ is taken into account. Thus, the frequency response is:
- $$H(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f)^2} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \tau}.$$
The two system parameters,
- the equivalent duration of the impulse $Δt = 1/Δf$ and
- the delay time $τ$,
can be taken from the impulse response $h(t)$ shown in the graph.
- It is obvious that this model does not correspond exactly to the (causal) reality since the impulse response $h(t)$ does not completely vanish even for $t < 0$ .
- Therefore, in subtask (3) the maximum relative error is aked for and defined as follows:
- $$\varepsilon_{\rm max} = \frac{\max_{t \hspace{0.02cm}< \hspace{0.1cm}0}|h(t)|}{h(t = \tau)}.$$
In words: The maximum relative error $ε_{\rm max}$ is equal to the maximum value of the impulse response $h(t)$ at negative times with respect to the maximum value $h(t = τ)$ of the impulse response.
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- In particular, reference is made to the page Gaussian low-pass filter.
- You can use the Gaussian (error) integral to calculate step and rectangle responses:
- $${\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$
Questions
Solution
- This is also the reciprocal of the equivalent impulse duration $Δt = 125 \ \rm ns$.
- The phase runtime $τ \hspace{0.15cm} \rm \underline{= \ 250 \ \rm ns}$ can be read directly from the graph, too.
(2) Without consideration of the runtime the result would be a cosine signal with the amplitude
- $$A_y = 1\,{\rm V} \cdot {\rm e}^{-\pi({ {6\,\rm MHz} }/{ {8\,\rm MHz} })^2}= 0.171\,{\rm V}.$$
- The runtime causes a phase shift of $3π$:
- $$ y(t) = A_y \cdot {\rm cos}(2\pi f_0 ( t - \tau) ) = A_y \cdot {\rm cos}(2\pi f_0 t - 2\pi \cdot {6\,\rm MHz}\cdot {250\,\rm ns} ) = A_y \cdot {\rm cos}(2\pi f_0 t - 3\pi ) = -A_y \cdot {\rm cos}(2\pi f_0 t ).$$
- Hence, the searched-for value is $y(t = 0) \hspace{0.05cm} \rm \underline{= \ –0.171 \ V}$.
(3) The impulse response is:
- $$h(t) = h_{\rm GTP}(t - \tau) =\Delta f \cdot {\rm e}^{-\pi(\frac{t - \tau}{\Delta t})^2} .$$
- Since $h(t)$ increases steadily in the range $t < 0$ the maximum value (at negative times) occurs approximately at $t = 0$ :
- $$h(t = 0) = \Delta f \cdot {\rm e}^{-\pi(\frac{ \tau}{\Delta t})^2}= \Delta f \cdot {\rm e}^{-4\pi} .$$
- Using $h(t = τ) = Δf$ the following is obtained:
- $$\varepsilon_{\rm max}= {\rm e}^{-4\pi}\hspace{0.15cm}\underline{ \approx 3.49} \cdot 10^{-6} .$$
(4) For the moment, we leave the phase runtime $τ$ of the second system out of consideration and compute the step response of the Gaussian low-pass filter:
- $$\sigma_{\rm GTP}(t) = \frac{1}{\Delta t} \cdot \int_{ -\infty }^{ t } {{\rm e}^{-\pi \left({t\hspace{0.05cm}'}/{\Delta t}\right)^2}} \hspace{0.1cm}{\rm d}t'.$$
- After the substitution $u = t\hspace{0.05cm}' \cdot {\sqrt{2\pi}}/{\Delta t}$ the following arises as a result with the Gaussian (error) integral $ϕ(x)$:
- $$\sigma_{\rm GTP}(t) = \frac{1}{\sqrt{2 \pi } } \cdot \int_{ -\infty }^{ \sqrt{2\pi}\cdot\hspace{0.05cm} t / \Delta t } { {\rm e}^{-u^2/2} } \hspace{0.1cm}{\rm d}u = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t}{\Delta t }),\hspace{1cm} {\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$
- Taking into account the runtime $τ$ one thus obtains for the total step response:
- $$\sigma(t) = \sigma_{\rm GTP}(t - \tau) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t - \tau}{\Delta t }).$$
- The value at $t = τ = 250 \ \rm ns$ is
- $$\sigma(t = {250\,\rm ns}) = \sigma_{\rm GTP}(t = 0) =\ \rm \underline{ϕ(0) \ = \ 0.500}.$$
- Accordingly, for $t = τ = 300 \ \rm ns$ the following is obtained:
- $$\sigma(t = {300\,\rm ns}) = \sigma_{\rm GTP}(t = {50\,\rm ns}) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{ {50\,\rm ns} }{ {125\,\rm ns} })\approx {\rm \phi}(1)\hspace{0.15cm}\underline{ = 0.841}.$$