Difference between revisions of "Aufgaben:Exercise 1.8Z: Cosine-Square Low-Pass Filter"
| (11 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory}} |
| − | }} | ||
| − | [[File:P_ID868__LZI_Z_1_8.png|right|frame| | + | [[File:P_ID868__LZI_Z_1_8.png|right|frame|Concerning the cosine-square low-pass filter]] |
| − | + | When studying digital systems a dirac-shaped input signal $x(t) = T \cdot \delta(t)$ is often assumed such that $X(f) = T$ holds. | |
| − | + | The output spectrum $Y(f)$ is then of equal form compared with the overall frequency response of the transmitter and receiver filter: | |
:$$H(f) = H_{\rm S}(f) \cdot H_{\rm E}(f).$$ | :$$H(f) = H_{\rm S}(f) \cdot H_{\rm E}(f).$$ | ||
| − | + | This frequency response is often assumed to be $\cos^2$-shaped (see graph): | |
| − | * | + | *For $f \cdot T \ge 1$ , $H(f) = 0$ holds. |
| − | * | + | *In the inner region the following holds: $H(f) = \cos^2(f \cdot T \cdot {\pi}/{ 2} ) .$ |
| − | + | Note that the equivalent bandwidth is $\Delta f = 1/{\Delta t}$ . Thus, for the equivalent ${\Delta t}$ of the impulse response one also obtains $T$ and the following holds: | |
:$$y(t) = T \cdot h(t) = {\rm si}(\pi \cdot {t}/{T} )\cdot \frac | :$$y(t) = T \cdot h(t) = {\rm si}(\pi \cdot {t}/{T} )\cdot \frac | ||
{\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2}.$$ | {\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2}.$$ | ||
| − | + | Also, note that the output signal $y(t)$ is dimensionless in cotrast to the impulse response $h(t)$ . This signal can also be represented as follows by applying trigonomic transformations: | |
:$$y(t) = {\pi}/{4} \cdot {\rm si}(\pi \cdot {t}/{T} )\cdot | :$$y(t) = {\pi}/{4} \cdot {\rm si}(\pi \cdot {t}/{T} )\cdot | ||
\big[ {\rm si}\big(\pi \cdot \left({t}/{T}+ 0.5 \right) | \big[ {\rm si}\big(\pi \cdot \left({t}/{T}+ 0.5 \right) | ||
| Line 24: | Line 23: | ||
\big)\big].$$ | \big)\big].$$ | ||
| − | + | For each of the following tasks select the equation that is easier to handle. | |
| − | + | For subtask '''(3)''' it shall be assumed that the signal $s(t)$ is a rectangular pulse in the middle between the two frequency responses $H_{\rm S}(f)$ and $H_{\rm S}(f)$ . Consequently, it must hold: | |
:$$H_{\rm E}(f) = {\rm si }(\pi f T ) .$$ | :$$H_{\rm E}(f) = {\rm si }(\pi f T ) .$$ | ||
| Line 36: | Line 35: | ||
| − | '' | + | ''Please note:'' |
| − | * | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory|Some Low-Pass Functions in Systems Theory]]. |
| − | * | + | *In particular, reference is made to the page [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Cosine–square_low-pass_filter|Cosine–square low-pass filter]]. |
| − | * | + | *You can check your results with the interactive applet [[Applets:Frequenzgang_und_Impulsantwort|Frequency response and impulse response]]. |
| Line 45: | Line 44: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Compute the output signal at times $t = 0$ and $t = T$. |
|type="{}"} | |type="{}"} | ||
$y(t = 0) \ = \ $ { 1 1% } | $y(t = 0) \ = \ $ { 1 1% } | ||
| Line 54: | Line 53: | ||
| − | { | + | {Compute the output signal at times $t = 0.5 T$ and $t = 1.5 T$. |
|type="{}"} | |type="{}"} | ||
$y(t = 0.5 T) \ = \ $ { 0.5 1% } | $y(t = 0.5 T) \ = \ $ { 0.5 1% } | ||
| Line 60: | Line 59: | ||
| − | { | + | {Compute $y(t)$ for large $t$-values. Suitable approximations are allowed and encouraged. What is the signal value at $t = 10.75 T$? |
|type="{}"} | |type="{}"} | ||
$y(t = 10.75 T) \ = \ $ { 32 1% } $ \ \cdot \ 10^{-6}$ | $y(t = 10.75 T) \ = \ $ { 32 1% } $ \ \cdot \ 10^{-6}$ | ||
| − | { | + | {State the required receiver frequency response $H_{\rm E}(f)$ for $H_{\rm S}(f)= {\rm si}(πfT)$ . What are the values for the given frequencies? |
|type="{}"} | |type="{}"} | ||
$H_{\rm E}(f=0) \ = \ $ { 1 1% } | $H_{\rm E}(f=0) \ = \ $ { 1 1% } | ||
| Line 75: | Line 74: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' From the first equation on the information page it directly follows that $y(t = 0) = 1$ and $y(t = T) = y(t = 2T) = \text{...} =0$ due to the $\rm si$–function. |
| − | * | + | *From the second equation these results are obtained, for example |
:$$y(t = 0) = {\pi}/{4} \cdot {\rm si}(0)\cdot \left[ {\rm | :$$y(t = 0) = {\pi}/{4} \cdot {\rm si}(0)\cdot \left[ {\rm | ||
si}(\pi/2)+ {\rm si}(-\pi/2)\right] | si}(\pi/2)+ {\rm si}(-\pi/2)\right] | ||
| Line 88: | Line 87: | ||
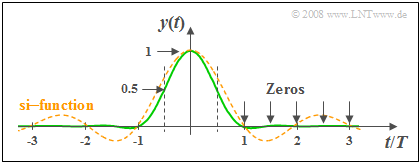
| − | [[File:EN_LZI_Z_1_8_b.png|right|frame| | + | [[File:EN_LZI_Z_1_8_b.png|right|frame|Output signal of the cosine-square low-pass filter]] |
| − | '''(2)''' | + | '''(2)''' The second representation is more suitable for the computation of these signal values: |
:$$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)\cdot \big[ {\rm | :$$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)\cdot \big[ {\rm | ||
si}(\pi)+ {\rm si}(0)\big].$$ | si}(\pi)+ {\rm si}(0)\big].$$ | ||
| − | * | + | *Considering ${\rm si}(0) = 1$ and ${\rm si}(\pi) = 0$ one obtains thus: |
:$$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)= {\pi}/{4} | :$$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)= {\pi}/{4} | ||
\cdot \frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{ = 0.5}.$$ | \cdot \frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{ = 0.5}.$$ | ||
| − | * | + | *Analogously, the following is obtained for $t = 1.5T$: |
:$$y(t = 1.5T) = {\pi}/{4} \cdot {\rm si}(3\pi/2)\cdot \left[ | :$$y(t = 1.5T) = {\pi}/{4} \cdot {\rm si}(3\pi/2)\cdot \left[ | ||
{\rm si}(2\pi)+ {\rm si}(\pi)\right] \hspace{0.15cm}\underline{ = 0}.$$ | {\rm si}(2\pi)+ {\rm si}(\pi)\right] \hspace{0.15cm}\underline{ = 0}.$$ | ||
| − | * | + | *Here, ${\rm si}(\pi) = {\rm si}(2\pi) = 0$ is considered. |
| − | * | + | *Also, at times $t/T = 2.5, 3.5,\text{ ... }$ , $y(t) = 0$ holds as shown in the above graph. |
| − | '''(3)''' | + | '''(3)''' For large values of $t$ the following holds by approximation (neglecting the "1" in the denominator): |
:$$y(t)= {\rm si}(\pi \cdot {t}/{T} )\cdot \frac | :$$y(t)= {\rm si}(\pi \cdot {t}/{T} )\cdot \frac | ||
{\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2} \approx \frac {\sin(\pi \cdot t / T )\cdot \cos(\pi \cdot t / T | {\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2} \approx \frac {\sin(\pi \cdot t / T )\cdot \cos(\pi \cdot t / T | ||
| Line 113: | Line 112: | ||
\cdot t / T )}{ 8 \pi \cdot( t/T )^3}.$$ | \cdot t / T )}{ 8 \pi \cdot( t/T )^3}.$$ | ||
| − | * | + | *This takes into account that $\sin(\alpha) \cdot \cos(\alpha) = \sin(2\alpha)/2$ . |
| − | * | + | *Hence at time $t = 10.75 T$ it holds that: |
:$$\sin(2\pi \cdot t / T ) = \sin (21.5\pi)= \sin (1.5\pi) = -1\hspace{0.3cm} | :$$\sin(2\pi \cdot t / T ) = \sin (21.5\pi)= \sin (1.5\pi) = -1\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} y(t = 10.75 T) = \frac {1 }{ 8 \pi \cdot( 10.75 )^3} \hspace{0.15cm}\underline{= 32 | \Rightarrow \hspace{0.3cm} y(t = 10.75 T) = \frac {1 }{ 8 \pi \cdot( 10.75 )^3} \hspace{0.15cm}\underline{= 32 | ||
| Line 120: | Line 119: | ||
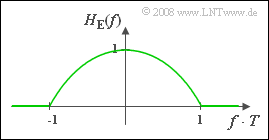
| − | [[File:P_ID872__LZI_Z_1_8_d.png|right|frame| | + | [[File:P_ID872__LZI_Z_1_8_d.png|right|frame|Searched-for receiver frequency response]] |
| − | '''(4)''' | + | '''(4)''' The receiver frequency response is the following for $|f \cdot T| \le 1$: |
:$$H_{\rm E}(f) = \frac{H(f)}{H_{\rm S}(f)}= \frac{\cos^2(\pi f T | :$$H_{\rm E}(f) = \frac{H(f)}{H_{\rm S}(f)}= \frac{\cos^2(\pi f T | ||
/2)}{{\rm si}(\pi fT)}.$$ | /2)}{{\rm si}(\pi fT)}.$$ | ||
| − | * | + | *This function curve is shown in the graph. The following holds or the interpolation values: |
:$$H_{\rm E}(f = 0) = \frac{\cos^2(0)}{{\rm si}(0)} \hspace{0.15cm}\underline{ = 1},$$ | :$$H_{\rm E}(f = 0) = \frac{\cos^2(0)}{{\rm si}(0)} \hspace{0.15cm}\underline{ = 1},$$ | ||
:$$H_{\rm E}(f = {0.5}/T \hspace{-0.15cm} = \hspace{-0.15cm} \frac{\cos^2(\pi/4)}{{\rm si}(\pi/2)}= (\sqrt{2} / 2)^2 \cdot \frac{\pi}{2} | :$$H_{\rm E}(f = {0.5}/T \hspace{-0.15cm} = \hspace{-0.15cm} \frac{\cos^2(\pi/4)}{{\rm si}(\pi/2)}= (\sqrt{2} / 2)^2 \cdot \frac{\pi}{2} | ||
| Line 130: | Line 129: | ||
:$$H_{\rm E}(f = {1}/{T}) = \frac{\cos^2(\pi/2)}{{\rm si}(\pi)} = "0/0"\hspace{0.15cm}\underline{= 0}.$$ | :$$H_{\rm E}(f = {1}/{T}) = \frac{\cos^2(\pi/2)}{{\rm si}(\pi)} = "0/0"\hspace{0.15cm}\underline{= 0}.$$ | ||
| − | + | This result takes into account that in the whole frequency domain $H_{\rm S}(f) \ge H(f) $ holds. Actually, the last calculated value should be determined by a limiting process in a mathematically exact way. We did that too, but not in this sample solution. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 20:43, 9 September 2021
When studying digital systems a dirac-shaped input signal $x(t) = T \cdot \delta(t)$ is often assumed such that $X(f) = T$ holds.
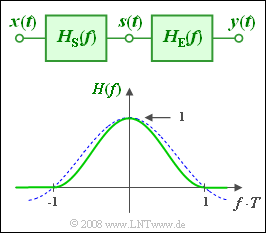
The output spectrum $Y(f)$ is then of equal form compared with the overall frequency response of the transmitter and receiver filter:
- $$H(f) = H_{\rm S}(f) \cdot H_{\rm E}(f).$$
This frequency response is often assumed to be $\cos^2$-shaped (see graph):
- For $f \cdot T \ge 1$ , $H(f) = 0$ holds.
- In the inner region the following holds: $H(f) = \cos^2(f \cdot T \cdot {\pi}/{ 2} ) .$
Note that the equivalent bandwidth is $\Delta f = 1/{\Delta t}$ . Thus, for the equivalent ${\Delta t}$ of the impulse response one also obtains $T$ and the following holds:
- $$y(t) = T \cdot h(t) = {\rm si}(\pi \cdot {t}/{T} )\cdot \frac {\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2}.$$
Also, note that the output signal $y(t)$ is dimensionless in cotrast to the impulse response $h(t)$ . This signal can also be represented as follows by applying trigonomic transformations:
- $$y(t) = {\pi}/{4} \cdot {\rm si}(\pi \cdot {t}/{T} )\cdot \big[ {\rm si}\big(\pi \cdot \left({t}/{T}+ 0.5 \right) \big)+ {\rm si}\big(\pi \cdot \left({t}/{T}- 0.5 \right) \big)\big].$$
For each of the following tasks select the equation that is easier to handle.
For subtask (3) it shall be assumed that the signal $s(t)$ is a rectangular pulse in the middle between the two frequency responses $H_{\rm S}(f)$ and $H_{\rm S}(f)$ . Consequently, it must hold:
- $$H_{\rm E}(f) = {\rm si }(\pi f T ) .$$
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- In particular, reference is made to the page Cosine–square low-pass filter.
- You can check your results with the interactive applet Frequency response and impulse response.
Questions
Solution
- From the second equation these results are obtained, for example
- $$y(t = 0) = {\pi}/{4} \cdot {\rm si}(0)\cdot \left[ {\rm si}(\pi/2)+ {\rm si}(-\pi/2)\right] {\pi}/{2} \cdot {\rm si}(\pi/2) = {\pi}/{2} \cdot \frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{= 1},$$
- $$y(t = T) \hspace{0.15cm}=\hspace{0.15cm}{\pi}/{4} \cdot {\rm si}(\pi)\cdot \left[ {\rm si}(3\pi/2)+ {\rm si}(\pi/2)\right] \hspace{0.15cm}\underline{= 0}.$$
(2) The second representation is more suitable for the computation of these signal values:
- $$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)\cdot \big[ {\rm si}(\pi)+ {\rm si}(0)\big].$$
- Considering ${\rm si}(0) = 1$ and ${\rm si}(\pi) = 0$ one obtains thus:
- $$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)= {\pi}/{4} \cdot \frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{ = 0.5}.$$
- Analogously, the following is obtained for $t = 1.5T$:
- $$y(t = 1.5T) = {\pi}/{4} \cdot {\rm si}(3\pi/2)\cdot \left[ {\rm si}(2\pi)+ {\rm si}(\pi)\right] \hspace{0.15cm}\underline{ = 0}.$$
- Here, ${\rm si}(\pi) = {\rm si}(2\pi) = 0$ is considered.
- Also, at times $t/T = 2.5, 3.5,\text{ ... }$ , $y(t) = 0$ holds as shown in the above graph.
(3) For large values of $t$ the following holds by approximation (neglecting the "1" in the denominator):
- $$y(t)= {\rm si}(\pi \cdot {t}/{T} )\cdot \frac {\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2} \approx \frac {\sin(\pi \cdot t / T )\cdot \cos(\pi \cdot t / T )}{ - (\pi \cdot t/T )(2 \cdot t/T )^2} = - \frac {\sin(2\pi \cdot t / T )}{ 8 \pi \cdot( t/T )^3}.$$
- This takes into account that $\sin(\alpha) \cdot \cos(\alpha) = \sin(2\alpha)/2$ .
- Hence at time $t = 10.75 T$ it holds that:
- $$\sin(2\pi \cdot t / T ) = \sin (21.5\pi)= \sin (1.5\pi) = -1\hspace{0.3cm} \Rightarrow \hspace{0.3cm} y(t = 10.75 T) = \frac {1 }{ 8 \pi \cdot( 10.75 )^3} \hspace{0.15cm}\underline{= 32 \cdot 10^{-6}}.$$
(4) The receiver frequency response is the following for $|f \cdot T| \le 1$:
- $$H_{\rm E}(f) = \frac{H(f)}{H_{\rm S}(f)}= \frac{\cos^2(\pi f T /2)}{{\rm si}(\pi fT)}.$$
- This function curve is shown in the graph. The following holds or the interpolation values:
- $$H_{\rm E}(f = 0) = \frac{\cos^2(0)}{{\rm si}(0)} \hspace{0.15cm}\underline{ = 1},$$
- $$H_{\rm E}(f = {0.5}/T \hspace{-0.15cm} = \hspace{-0.15cm} \frac{\cos^2(\pi/4)}{{\rm si}(\pi/2)}= (\sqrt{2} / 2)^2 \cdot \frac{\pi}{2} = \hspace{-0.15cm} \frac{\pi}{4}\hspace{0.15cm}\underline{ \approx 0.785},$$
- $$H_{\rm E}(f = {1}/{T}) = \frac{\cos^2(\pi/2)}{{\rm si}(\pi)} = "0/0"\hspace{0.15cm}\underline{= 0}.$$
This result takes into account that in the whole frequency domain $H_{\rm S}(f) \ge H(f) $ holds. Actually, the last calculated value should be determined by a limiting process in a mathematically exact way. We did that too, but not in this sample solution.