Difference between revisions of "Aufgaben:Exercise 2.10: Reed-Solomon Error Detection"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes}} |
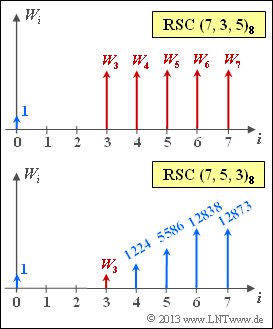
| − | [[File: P_ID2524__KC_A_2_10.png|right|frame| | + | [[File: P_ID2524__KC_A_2_10.png|right|frame|Distance spectra of two different Reed-Solomon codes]] |
| − | + | For a linear block code, up to $e = d_{\rm min} - 1$ errors can be detected. For all Reed–Solomon codes the minimum distance is | |
:$$d_{\rm min} = n-k+1 \hspace{0.05cm}.$$ | :$$d_{\rm min} = n-k+1 \hspace{0.05cm}.$$ | ||
| − | + | One must distinguish the following cases: | |
| − | * | + | * If no more than $e = n - k$ symbol errors occur, the block is always detected as faulty. |
| − | * | + | * Error detection can still work even if more than $n - k$ symbol errors occur, and this is when the received word is not a valid codeword of the Reed–Solomon code: |
:$$\underline {y} \notin C_{\rm RS} = \{ \underline {c}_{\hspace{0.05cm}0}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_i, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_{\hspace{0.05cm}n -1} \} | :$$\underline {y} \notin C_{\rm RS} = \{ \underline {c}_{\hspace{0.05cm}0}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_i, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_{\hspace{0.05cm}n -1} \} | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | * However, if the corrupted received word $(\underline{y} ≠ \underline{c})$ is a valid codeword ⇒ $\underline{y}$, the decoding process will leave the corrupted block undetected. |
| − | + | We define as block error probability: | |
:$${\rm Pr}({\rm Blockfehler}) = {\rm Pr}(\underline {y} \ne \underline {c}) | :$${\rm Pr}({\rm Blockfehler}) = {\rm Pr}(\underline {y} \ne \underline {c}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In | + | In this exercise, this probability is to be determined for the following codes: |
| − | * Reed–Solomon | + | * Reed–Solomon code $(7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5$, |
| − | * Reed–Solomon | + | * Reed–Solomon code $(7, \, 5, \, 3)_8 \ \Rightarrow \ d_{\rm min} = 3$. |
| − | + | Furthermore, let it hold: | |
| − | * | + | * Each symbol is corrupted into another symbol with probability $\varepsilon_{\rm S} = 0.1$ and correctly transferred with probability $1 - \varepsilon_{\rm S} = 0.9$ . |
| − | * | + | * For the distance spectrum of a Reed–Solomon code of length $n$ holds with $d = d_{\rm min}$: |
:$$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$ | :$$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$ | ||
| − | + | Besides, two bounds for the block error probability will be considered and evaluated: | |
| − | * | + | * If the minimum distance alone is known, one can derive an <i>upper bound</i> from it. The weight enumerating factors $W_i$ are to be chosen in such a way, that certainly (that is: with all constellations) applies: |
| − | :$${\rm Pr}({\rm | + | :$${\rm Pr}({\rm Upper\hspace{0.15cm} bound}) \ge {\rm Pr}({\rm Block\hspace{0.15cm}error}) |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | * A <i>lower bound</i> additionally requires knowledge of the weight function $W_i$ for $i = d_{\rm min}$. Thus, the following condition can be satisfied: |
| − | :$${\rm Pr}({\rm | + | :$${\rm Pr}({\rm Upper\hspace{0.15cm} bound}) \le {\rm Pr}({\rm Block\hspace{0.15cm}error}) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 42: | Line 42: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes|"Definition and Properties of Reed-Solomon Codes"]]. |
| − | * | + | *Reference is made in particular to the page [[Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes#Singleton_bound_and_minimum_distance|"Singleton Bound and Minimum Distance"]]. |
| − | * | + | * To be calculated are the weights marked in red in the above graph $W_i$. |
| Line 51: | Line 51: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the distance spectrum for the $\rm RSC \, (7, \, 3, \, 5)_8$. |
|type="{}"} | |type="{}"} | ||
$W_3 \ = \ ${ 0. } | $W_3 \ = \ ${ 0. } | ||
| Line 61: | Line 61: | ||
$W_7 \ = \ ${ 217 } | $W_7 \ = \ ${ 217 } | ||
| − | { | + | {What is the missing weight of the $\rm RSC \, (7, \, 5, \, 3)_8$ in the graph? |
|type="{}"} | |type="{}"} | ||
$W_3 \ = \ ${ 245 } | $W_3 \ = \ ${ 245 } | ||
| − | { | + | {What is the probability that an incorrect block remains undetected? Let the corruption probability of each symbol be $\varepsilon = 0.1$. |
|type="{}"} | |type="{}"} | ||
$\rm RSC \, (7, \, 3, \, 5) \text{:} \hspace{0.4cm} Pr(Blockfehler) \ = \ ${ 0.263 3% } $\ \cdot 10^{-5}$ | $\rm RSC \, (7, \, 3, \, 5) \text{:} \hspace{0.4cm} Pr(Blockfehler) \ = \ ${ 0.263 3% } $\ \cdot 10^{-5}$ | ||
$\rm RSC \, (7, \, 5, \, 3) \text{:} \hspace{0.4cm} Pr(Blockfehler) \ = \ ${ 0.942 3% } $\ \cdot 10^{-5}$ | $\rm RSC \, (7, \, 5, \, 3) \text{:} \hspace{0.4cm} Pr(Blockfehler) \ = \ ${ 0.942 3% } $\ \cdot 10^{-5}$ | ||
| − | { | + | {Calculate and evaluate for both codes the upper bound proposed in the specification $p_{\rm upper} = \rm Pr(Upper \ bound)$. |
|type="{}"} | |type="{}"} | ||
${\rm RSC} \, (7, \, 3, \, 5) \text{:} \hspace{0.4cm} p_{\rm oben} \ = \ ${ 0.81 3% } $\ \cdot 10^{-5}$ | ${\rm RSC} \, (7, \, 3, \, 5) \text{:} \hspace{0.4cm} p_{\rm oben} \ = \ ${ 0.81 3% } $\ \cdot 10^{-5}$ | ||
${\rm RSC} \, (7, \, 5, \, 3) \text{:} \hspace{0.4cm} p_{\rm oben} \ = \ ${ 65.6 3% } $\ \cdot 10^{-5}$ | ${\rm RSC} \, (7, \, 5, \, 3) \text{:} \hspace{0.4cm} p_{\rm oben} \ = \ ${ 65.6 3% } $\ \cdot 10^{-5}$ | ||
| − | { | + | {Calculate and evaluate for both codes the lower bound proposed in the specification $p_{\rm lower} = \rm Pr(Lower \ bound)$. |
|type="{}"} | |type="{}"} | ||
${\rm RSC} \, (7, \, 3, \, 5) \text{:} \hspace{0.4cm} p_{\rm unten} \ = \ ${ 0.233 3% } $\ \cdot 10^{-5}$ | ${\rm RSC} \, (7, \, 3, \, 5) \text{:} \hspace{0.4cm} p_{\rm unten} \ = \ ${ 0.233 3% } $\ \cdot 10^{-5}$ | ||
| Line 81: | Line 81: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Die Gleichung zur Beschreibung der Gewichte $W_i$ lautet (die minimale Distanz $d_{\rm min}$ ist hier mit $d$ abgekürzt): | '''(1)''' Die Gleichung zur Beschreibung der Gewichte $W_i$ lautet (die minimale Distanz $d_{\rm min}$ ist hier mit $d$ abgekürzt): | ||
Revision as of 19:24, 2 September 2022
For a linear block code, up to $e = d_{\rm min} - 1$ errors can be detected. For all Reed–Solomon codes the minimum distance is
- $$d_{\rm min} = n-k+1 \hspace{0.05cm}.$$
One must distinguish the following cases:
- If no more than $e = n - k$ symbol errors occur, the block is always detected as faulty.
- Error detection can still work even if more than $n - k$ symbol errors occur, and this is when the received word is not a valid codeword of the Reed–Solomon code:
- $$\underline {y} \notin C_{\rm RS} = \{ \underline {c}_{\hspace{0.05cm}0}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_i, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_{\hspace{0.05cm}n -1} \} \hspace{0.05cm}. $$
- However, if the corrupted received word $(\underline{y} ≠ \underline{c})$ is a valid codeword ⇒ $\underline{y}$, the decoding process will leave the corrupted block undetected.
We define as block error probability:
- $${\rm Pr}({\rm Blockfehler}) = {\rm Pr}(\underline {y} \ne \underline {c}) \hspace{0.05cm}.$$
In this exercise, this probability is to be determined for the following codes:
- Reed–Solomon code $(7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5$,
- Reed–Solomon code $(7, \, 5, \, 3)_8 \ \Rightarrow \ d_{\rm min} = 3$.
Furthermore, let it hold:
- Each symbol is corrupted into another symbol with probability $\varepsilon_{\rm S} = 0.1$ and correctly transferred with probability $1 - \varepsilon_{\rm S} = 0.9$ .
- For the distance spectrum of a Reed–Solomon code of length $n$ holds with $d = d_{\rm min}$:
- $$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$
Besides, two bounds for the block error probability will be considered and evaluated:
- If the minimum distance alone is known, one can derive an upper bound from it. The weight enumerating factors $W_i$ are to be chosen in such a way, that certainly (that is: with all constellations) applies:
- $${\rm Pr}({\rm Upper\hspace{0.15cm} bound}) \ge {\rm Pr}({\rm Block\hspace{0.15cm}error}) \hspace{0.05cm}. $$
- A lower bound additionally requires knowledge of the weight function $W_i$ for $i = d_{\rm min}$. Thus, the following condition can be satisfied:
- $${\rm Pr}({\rm Upper\hspace{0.15cm} bound}) \le {\rm Pr}({\rm Block\hspace{0.15cm}error}) \hspace{0.05cm}.$$
Hints:
- The exercise belongs to the chapter "Definition and Properties of Reed-Solomon Codes".
- Reference is made in particular to the page "Singleton Bound and Minimum Distance".
- To be calculated are the weights marked in red in the above graph $W_i$.
Questions
Solution
- $$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$
Wegen der minimalen Distanz $d_{\min} = 5$ sind $W_3 \ \underline{= 0}$ und $W_4 \ \underline{= 0}$. Die weiteren Gewichte ergeben sich zu
- $$W_5 = {7 \choose 5} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 \cdot4 \cdot 3}{1 \cdot 2 \cdot 3 \cdot4 \cdot 5} \cdot 7 = 21 \cdot 7 \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$
- $$W_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 6} \cdot \sum_{j = 0}^{1}\hspace{0.15cm}(-1)^j \cdot {6 \choose j} \cdot \big (\hspace{0.03cm}8^{2\hspace{0.03cm}-\hspace{0.03cm}j} -1 \big )=7 \cdot \left [ (8^2 - 1) - 6 \cdot (8^1 - 1)\right ] = 7 \cdot (63-42) \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$
- $$W_7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 7} \cdot \sum_{j = 0}^{2}\hspace{0.15cm}(-1)^j \cdot {7 \choose j} \cdot \big (\hspace{0.03cm}8^{3\hspace{0.03cm}-\hspace{0.03cm}j} -1 \big )= (8^3 - 1) - 7 \cdot (8^2 - 1) +21 \cdot (8^1 - 1) = 511 - 7 \cdot 63 + 21 \cdot 7 \hspace{0.15cm}\underline {= 217}\hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm}W_0 + W_5 + W_6 + W_7 = 1 + 147 + 147 + 217 = 512 = 8^3 = q^k\hspace{0.05cm}.$$
(2) Analog zur Teilaufgabe (1) erhält man:
- $$W_3 = {7 \choose 3} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 }{1 \cdot 2 \cdot 3 } \cdot 7 = 35 \cdot 7 \hspace{0.15cm}\underline {= 245}\hspace{0.05cm}.$$
(3) Die Verfälschungswahrscheinlichkeit eines Symbols ist mit $\varepsilon_{\rm S} = 0.1$ gegeben.
- Dann gilt für die Wahrscheinlichkeit, dass in einem Codewort mit $n = 7$ Codesymbolen
- genau 3 Symbole verfälscht werden:
- $$p_3 = 0.1^3 \cdot 0.9^4 = 0.6561 \cdot 10^{-3} \hspace{0.05cm},$$
- genau 4 Symbole verfälscht werden:
- $$p_4 = 0.1^4 \cdot 0.9^3 = 0.729 \cdot 10^{-4} \hspace{0.05cm},$$
- genau 5 Symbole verfälscht werden:
- $$p_5 = 0.1^5 \cdot 0.9^2 = 0.81 \cdot 10^{-5} \hspace{0.05cm},$$
- genau 6 Symbole verfälscht werden:
- $$p_6 = 0.1^6 \cdot 0.9 = 0.9 \cdot 10^{-6}\hspace{0.05cm},$$
- alle $n = 7$ Symbole verfälscht werden:
- $$p_7 = 0.1^7 = 10^{-7}\hspace{0.05cm}.$$
Beim $\rm RSC \, (7, \, 3, \, 5)_8$ kann das Nullwort durch Symbolfehler in eines von $q^k - 1 = 8^3 - 1 = 511$ anderen Codeworten verfälscht werden.
Damit erhält man mit den Gewichtsfunktionen von Teilaufgabe (1):
- $${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{511} =\frac {147 \cdot 0.81 \cdot 10^{-5} + 147 \cdot 0.9 \cdot 10^{-6} + 217 \cdot 10^{-7}}{511} \hspace{0.15cm}\underline {\approx 0.263 \cdot 10^{-5}} \hspace{0.05cm}.$$
Beim $\rm RSC \, (7, \, 5, \, 3)_8$ muss wegen $k = 5$ über $8^5 - 1 = 32767$ Verfälschungswahrscheinlichkeiten gemittelt werden.
Mit $W_3 = 245$ aus Teilaufgabe (2) und den Gewichten $W_4 = 1224, \ W_5 = 5586, \ W_6 = 12838, \ W_7 = 12873$ gemäß Angabenblatt erhält man hierfür:
- $${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_3 \cdot p_3 + W_4 \cdot p_4 + W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{32767} =\frac {245 \cdot 0.656 \cdot 10^{-3} + \hspace{0.15cm}... \hspace{0.15cm}+ 12873 \cdot 10^{-7}}{32767} \hspace{0.15cm}\underline {\approx 0.942 \cdot 10^{-5}} \hspace{0.05cm}. $$
(4) Bekannt sei nur $d_{\rm min}$ (weiter mit $d$ abgekürzt) und damit auch $p_d = \varepsilon_{\rm S}^d \cdot (1 - \varepsilon_{\rm S})^{n-d}$. Dies ist gleichzeitig die gesuchte obere Schranke:
- ${\rm RSC} \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} {\rm Pr(Obere \ Schranke)} = p_5 = \underline{0.81 \cdot 10^{-5}}$,
- ${\rm RSC} \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} {\rm Pr(Obere \ Schranke)} = p_3 = \underline{65.6 \cdot 10^{-5}}$.
Da das Gewicht $W_d$ als nicht bekannt vorausgesetzt wurde, setzt man dieses auf den maximal möglichen Wert ($W_5 = 511$ bzw. $W_3 = 32767$), so dass die Vorfaktoren in den Gleichungen zur Teilaufgabe (3) verschwinden. Nur so ist eine obere Schranke sichergestellt.
Die obere Schranke liegt in beiden Fällen deutlich über den Ergebnissen der Teilaufgabe (3):
- $\rm RSC \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} 0.810 \cdot 10^{-5}$ statt $0.263 \cdot 10^{-5}$ (Faktor ca. $3$),
- $\rm RSC \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} 65.6 \cdot 10^{-5}$ statt $0.942 \cdot 10^{-5}$ (Faktor ca. $70$).
(5) Mit der Abkürzung $d = d_{\rm min}$ erhält man für die untere Schranke:
- $${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke})= \frac{W_d \cdot p_d}{q^k -1} \hspace{0.05cm}. $$
- Für den $\rm RSC \, (7, \, 3, \, 5)_8$ liegt wegen $W_d = W_5$ und $p_d = p_5$ die unter Schranke um etwa $11\%$ unterhalb des tatsächlichen Wertes $(0.263 \cdot 10^{-5})$:
- $${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) = \frac{147 \cdot 0.81 \cdot 10^{-5}}{511} \hspace{0.15cm}\underline {\approx 0.233 \cdot 10^{-5}}$$
- Für den $\rm RSC \, (7, \, 5, \, 3)_8$ gilt mit $W_d = W_3$ und $p_d = p_3$ weicht die untere Schranke hier vom tatsächlichen Wert $(0.942 \cdot 10^{-5})$stärker ab, weil bei diesem Code die Beiträge der höheren Gewichte $(W_4, \ W_5, \ W_6, \ W_7)$ in Relation zu $W_3$ relevanter sind:
- $${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) = \frac{245 \cdot 0.656 \cdot 10^{-3}}{32767} \hspace{0.15cm}\underline {\approx 0.494 \cdot 10^{-5}}\hspace{0.05cm}.$$