Difference between revisions of "Aufgaben:Exercise 2.1: DSB-AM with Cosine? Or with Sine?"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/ Zweiseitenband-Amplitudenmodula }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice…“) |
m |
||
| (32 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Double-Sideband_Amplitude_Modulation |
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID985__Mod_A_2_1.png|right|frame|Spectrum of the analytical signal]] |
| + | Let us consider the amplitude modulation of the source signal $q(t)$ with the carrier signal $z(t)$. These signals are given by: | ||
| + | :$$q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N})\hspace{0.05cm},$$ | ||
| + | :$$z(t) = \hspace{0.15cm}1 \hspace{0.13cm} \cdot \hspace{0.1cm}\cos(2 \pi f_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$ | ||
| + | The carrier frequency is known to be $f_{\rm T} = 40\text{ kHz}$. The other system parameters $A_{\rm N}$, $f_{\rm N}$, $ϕ_{\rm N}$ and $ϕ_{\rm T}$ are to be determined in this exercise. | ||
| + | *The subscript "N" refers to the message signal (German: "Nachrichtensignal") $q(t)$ | ||
| + | *and "T" to the carrier (German: "Trägersignal") $z(t)$. | ||
| − | === | + | |
| + | The spectrum $S_+(f)$ of the analytical signal $s_+(t)$ at the modulator output is also given (see graph): | ||
| + | :$$S_+(f) = {\rm j}\cdot 2\,{\rm V} \cdot \delta ( f - f_{30} )+ {\rm j}\cdot 2\,{\rm V} \cdot \delta ( f - f_{50} )\hspace{0.05cm}.$$ | ||
| + | Here, the abbreviations $f_{30} = 30\text{ kHz}$ and $f_{50} = 50\text{ kHz}$ are used. | ||
| + | |||
| + | As a reminder: The spectrum $S_+(f)$ is obtained from $S(f)$ by | ||
| + | *truncating the components at negative frequencies and | ||
| + | *doubling positive frequencies. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *This exercise belongs to the chapter [[Modulation_Methods/Double-Sideband_Amplitude_Modulation|Double-Sideband Amplitude Modulation]]. | ||
| + | *Particular reference will be made to the pages [[Modulation_Methods/Double-Sideband_Amplitude_Modulation#Description_in_the_frequency_domain|Description in the frequency domain]] and [[Modulation_Methods/Double-Sideband_Amplitude_Modulation#Description_in_the_time_domain|Description in the time domain]]. | ||
| + | *The following trigonometric identities are given: | ||
| + | :$$\cos(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \big[ \cos(\alpha-\beta) + \cos(\alpha+\beta)\big ] \hspace{0.05cm}, \hspace{0.5cm} \cos(90^{\circ}- \hspace{0.05cm} \alpha) = \sin(\alpha) \hspace{0.05cm}, \hspace{0.5cm} \cos(90^{\circ}+ \hspace{0.05cm} \alpha) = -\sin(\alpha) \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Find the spectrum $S(f)$. Which of the following statements are correct? |
|type="[]"} | |type="[]"} | ||
| − | - | + | + $S(f)$ consists of four Dirac delta functions. |
| − | + | + | - All Dirac weights have the same magnitude $2\text{ V}$. |
| + | + All Dirac weights are imaginary. | ||
| + | |||
| + | |||
| + | {What is the modulated signal $s(t)$? Which statement is true? | ||
| + | |type="()"} | ||
| + | + It is DSB-AM without carrier ⇒ "DSB-AM with carrier suppression". | ||
| + | - It is DSB-AM with carrier. | ||
| + | {State the message signal frequency $f_{\rm N}$. | ||
| + | |type="{}"} | ||
| + | $f_{\rm N} \ = \ $ { 10 3% } $\ \text{kHz}$ | ||
| − | { | + | {Determine the phases of the two signals. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $ϕ_{\rm N} \ = \ $ { 0. } $\ \text{degrees}$ |
| + | $ϕ_{\rm T} \ = \ $ { 90 } $\ \text{degrees}$ | ||
| + | {What is the amplitude of the message signal? | ||
| + | |type="{}"} | ||
| + | $A_{\rm N} \ = \ $ { 4 3% } $\ \text{V}$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' <u>Answers 1 and 3</u> are correct: |
| − | '''2 | + | *At positive frequencies, $S_+(f)$ is obtained from $S(f)$ by doubling. |
| − | '''3 | + | *It follows that the impulse weights of $S(f)$ are each only ${\rm j} · 1 \text{ V}$. |
| − | '''4.''' | + | *Because of the Assignment Theorem, $S(f)$ must be an odd function. |
| − | '''5 | + | *Therefore, $S(f)$ has two more Dirac delta functions at $f = -f_{30}$ and $f = -f_{50}$, each with weight $-{\rm j} · 1 \text{ V}$: |
| − | ''' | + | :$$S(f) = 1\,{\rm V} \cdot \big[ {\rm j}\cdot \delta ( f - f_{30} )-{\rm j} \cdot \delta ( f + f_{30} )+ {\rm j} \cdot \delta ( f - f_{50} )-{\rm j} \cdot \delta ( f + f_{50} )\big] \hspace{0.05cm}.$$ |
| − | ''' | + | |
| + | |||
| + | |||
| + | '''(2)''' The inverse Fourier transform of $S(f)$ with $ω_{30} = 2π · f_{30}$ and $ω_{50} = 2πf_{50}$ leads to the following signal: | ||
| + | :$$ s(t) = -2\,{\rm V} \cdot \sin(\omega_{\rm 30} t )-2\,{\rm V} \cdot \sin(\omega_{\rm 50} t )\hspace{0.05cm}.$$ | ||
| + | *This does not contain any component at the carrier frequency $f_{\rm T} = 40\text{ kHz}$, so the <u>first statement</u> is true. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' For DSB–AM without carrier, $s(t)$ includes only the two frequencies $f_{\rm T} – f_{\rm N}$ and $f_{\rm T} + f_{\rm N}$. | ||
| + | *Hence, with $f_{\rm T} = 40\text{ kHz}$ for the message frequency, it follows that $f_{\rm N} \hspace{0.05cm}\underline {= 10\ \rm kHz}.$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' For DSB–AM without carrier, it holds that: | ||
| + | :$$s(t) = q(t) \cdot z(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} t + \phi_{\rm N})\cdot \cos(\omega_{\rm T} t + \phi_{\rm T})$$ | ||
| + | :$$\Rightarrow \hspace{0.5cm} s(t) = \frac{A_{\rm N}}{2} \cdot \left[ \cos\left((\omega_{\rm T} +\omega_{\rm N})\cdot t + \phi_{\rm T}+ \phi_{\rm N}\right) + \cos\left((\omega_{\rm T} -\omega_{\rm N})\cdot t + \phi_{\rm T}- \phi_{\rm N}\right) \right] \hspace{0.05cm}.$$ | ||
| + | *A comparison with the result from subtask '''(2)''' shows that: | ||
| + | :$$\cos(\omega_{\rm 30} \cdot t + \phi_{\rm T}- \phi_{\rm N}) = -\sin(\omega_{\rm 30} \cdot t )\hspace{0.05cm},$$ | ||
| + | :$$\cos(\omega_{\rm 50} \cdot t + \phi_{\rm T}+ \phi_{\rm N}) = -\sin(\omega_{\rm 50} \cdot t ) \hspace{0.05cm}.$$ | ||
| + | *Both equations can only be satisfied simultaneously with phase $ϕ_{\rm N} \hspace{0.05cm}\underline {= 0}$ . | ||
| + | *Additionally, from the last given trigonometric relation it follows that $ϕ_{\rm T} \hspace{0.05cm}\underline {= 90^\circ} = π/2$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Comparing the results from subtasks '''(2)''' and '''(4)''' leads to $A_{\rm N} \hspace{0.05cm}\underline {= 4 \ \rm V}$. Thus, the equations of the signals involved in the modulation are: | ||
| + | :$$q(t ) = 4\,{\rm V} \cdot \cos (2 \pi \cdot 10\,{\rm kHz} \cdot t) \hspace{0.05cm},$$ | ||
| + | :$$z(t) = 1 \cdot \cos (2 \pi \cdot 40\,{\rm kHz} \cdot t + 90^{\circ}) = -\sin (2 \pi \cdot 40\,{\rm kHz} \cdot t )\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^2.1 Double Sideband Amplitude Modulation^]] |
Latest revision as of 17:31, 24 March 2022
Let us consider the amplitude modulation of the source signal $q(t)$ with the carrier signal $z(t)$. These signals are given by:
- $$q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N})\hspace{0.05cm},$$
- $$z(t) = \hspace{0.15cm}1 \hspace{0.13cm} \cdot \hspace{0.1cm}\cos(2 \pi f_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$
The carrier frequency is known to be $f_{\rm T} = 40\text{ kHz}$. The other system parameters $A_{\rm N}$, $f_{\rm N}$, $ϕ_{\rm N}$ and $ϕ_{\rm T}$ are to be determined in this exercise.
- The subscript "N" refers to the message signal (German: "Nachrichtensignal") $q(t)$
- and "T" to the carrier (German: "Trägersignal") $z(t)$.
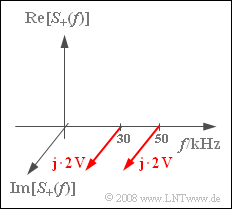
The spectrum $S_+(f)$ of the analytical signal $s_+(t)$ at the modulator output is also given (see graph):
- $$S_+(f) = {\rm j}\cdot 2\,{\rm V} \cdot \delta ( f - f_{30} )+ {\rm j}\cdot 2\,{\rm V} \cdot \delta ( f - f_{50} )\hspace{0.05cm}.$$
Here, the abbreviations $f_{30} = 30\text{ kHz}$ and $f_{50} = 50\text{ kHz}$ are used.
As a reminder: The spectrum $S_+(f)$ is obtained from $S(f)$ by
- truncating the components at negative frequencies and
- doubling positive frequencies.
Hints:
- This exercise belongs to the chapter Double-Sideband Amplitude Modulation.
- Particular reference will be made to the pages Description in the frequency domain and Description in the time domain.
- The following trigonometric identities are given:
- $$\cos(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \big[ \cos(\alpha-\beta) + \cos(\alpha+\beta)\big ] \hspace{0.05cm}, \hspace{0.5cm} \cos(90^{\circ}- \hspace{0.05cm} \alpha) = \sin(\alpha) \hspace{0.05cm}, \hspace{0.5cm} \cos(90^{\circ}+ \hspace{0.05cm} \alpha) = -\sin(\alpha) \hspace{0.05cm}.$$
Questions
Solution
- At positive frequencies, $S_+(f)$ is obtained from $S(f)$ by doubling.
- It follows that the impulse weights of $S(f)$ are each only ${\rm j} · 1 \text{ V}$.
- Because of the Assignment Theorem, $S(f)$ must be an odd function.
- Therefore, $S(f)$ has two more Dirac delta functions at $f = -f_{30}$ and $f = -f_{50}$, each with weight $-{\rm j} · 1 \text{ V}$:
- $$S(f) = 1\,{\rm V} \cdot \big[ {\rm j}\cdot \delta ( f - f_{30} )-{\rm j} \cdot \delta ( f + f_{30} )+ {\rm j} \cdot \delta ( f - f_{50} )-{\rm j} \cdot \delta ( f + f_{50} )\big] \hspace{0.05cm}.$$
(2) The inverse Fourier transform of $S(f)$ with $ω_{30} = 2π · f_{30}$ and $ω_{50} = 2πf_{50}$ leads to the following signal:
- $$ s(t) = -2\,{\rm V} \cdot \sin(\omega_{\rm 30} t )-2\,{\rm V} \cdot \sin(\omega_{\rm 50} t )\hspace{0.05cm}.$$
- This does not contain any component at the carrier frequency $f_{\rm T} = 40\text{ kHz}$, so the first statement is true.
(3) For DSB–AM without carrier, $s(t)$ includes only the two frequencies $f_{\rm T} – f_{\rm N}$ and $f_{\rm T} + f_{\rm N}$.
- Hence, with $f_{\rm T} = 40\text{ kHz}$ for the message frequency, it follows that $f_{\rm N} \hspace{0.05cm}\underline {= 10\ \rm kHz}.$
(4) For DSB–AM without carrier, it holds that:
- $$s(t) = q(t) \cdot z(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} t + \phi_{\rm N})\cdot \cos(\omega_{\rm T} t + \phi_{\rm T})$$
- $$\Rightarrow \hspace{0.5cm} s(t) = \frac{A_{\rm N}}{2} \cdot \left[ \cos\left((\omega_{\rm T} +\omega_{\rm N})\cdot t + \phi_{\rm T}+ \phi_{\rm N}\right) + \cos\left((\omega_{\rm T} -\omega_{\rm N})\cdot t + \phi_{\rm T}- \phi_{\rm N}\right) \right] \hspace{0.05cm}.$$
- A comparison with the result from subtask (2) shows that:
- $$\cos(\omega_{\rm 30} \cdot t + \phi_{\rm T}- \phi_{\rm N}) = -\sin(\omega_{\rm 30} \cdot t )\hspace{0.05cm},$$
- $$\cos(\omega_{\rm 50} \cdot t + \phi_{\rm T}+ \phi_{\rm N}) = -\sin(\omega_{\rm 50} \cdot t ) \hspace{0.05cm}.$$
- Both equations can only be satisfied simultaneously with phase $ϕ_{\rm N} \hspace{0.05cm}\underline {= 0}$ .
- Additionally, from the last given trigonometric relation it follows that $ϕ_{\rm T} \hspace{0.05cm}\underline {= 90^\circ} = π/2$.
(5) Comparing the results from subtasks (2) and (4) leads to $A_{\rm N} \hspace{0.05cm}\underline {= 4 \ \rm V}$. Thus, the equations of the signals involved in the modulation are:
- $$q(t ) = 4\,{\rm V} \cdot \cos (2 \pi \cdot 10\,{\rm kHz} \cdot t) \hspace{0.05cm},$$
- $$z(t) = 1 \cdot \cos (2 \pi \cdot 40\,{\rm kHz} \cdot t + 90^{\circ}) = -\sin (2 \pi \cdot 40\,{\rm kHz} \cdot t )\hspace{0.05cm}.$$