Difference between revisions of "Aufgaben:Exercise 2.2Z: Galois Field GF(5)"
From LNTwww
| Line 2: | Line 2: | ||
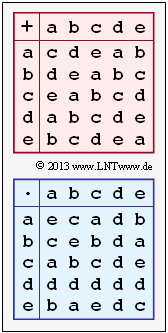
[[File:P_ID2494__KC_Z_2_2.png|right|frame|Additions– und Multiplikationstabelle für $\{a, \, b, \, c, \, d, \, e\}$]] | [[File:P_ID2494__KC_Z_2_2.png|right|frame|Additions– und Multiplikationstabelle für $\{a, \, b, \, c, \, d, \, e\}$]] | ||
| − | Wie in [[Aufgabe A2.2]] betrachten wir einen endlichen Körper der Ordnung $q = 5$ und damit das Galoisfeld | + | Wie in [[Aufgaben:2.2_Eigenschaften_von_Galoisfeldern|Aufgabe A2.2]] betrachten wir einen endlichen Körper der Ordnung $q = 5$ und damit das Galoisfeld |
:$${\rm GF}(5) = \{{a}, { b},{c},{d},{e}\}\hspace{0.05cm}.$$ | :$${\rm GF}(5) = \{{a}, { b},{c},{d},{e}\}\hspace{0.05cm}.$$ | ||
| Line 9: | Line 9: | ||
* eine Multiplikationstabelle modulo 5, | * eine Multiplikationstabelle modulo 5, | ||
| − | Die wichtigsten Eigenschaften eines Galoisfeldes sind auf [[Theorieseite 1]] zusammengestellt. In dieser Aufgabe wird Bezug genommen auf | + | Die wichtigsten Eigenschaften eines Galoisfeldes sind auf [[Kanalcodierung/Einige_Grundlagen_der_Algebra#Definition_eines_Galoisfeldes|Theorieseite 1]] zusammengestellt. In dieser Aufgabe wird Bezug genommen auf |
* das Kommutativ– und das Distributivgesetz, | * das Kommutativ– und das Distributivgesetz, | ||
* die neutralen Elemente von Addition und Multiplikation, | * die neutralen Elemente von Addition und Multiplikation, | ||
Revision as of 10:48, 15 December 2017
Additions– und Multiplikationstabelle für $\{a, \, b, \, c, \, d, \, e\}$
Wie in Aufgabe A2.2 betrachten wir einen endlichen Körper der Ordnung $q = 5$ und damit das Galoisfeld
- $${\rm GF}(5) = \{{a}, { b},{c},{d},{e}\}\hspace{0.05cm}.$$
Über die Elemente werden weiter keine Aussagen getroffen. Es können sowohl ganze Zahlen sein oder irgendwelche mathematische Ausdrücke. Das Galoisfeld wird ausschließlich bestimmt durch
- eine Additionstabelle modulo 5,
- eine Multiplikationstabelle modulo 5,
Die wichtigsten Eigenschaften eines Galoisfeldes sind auf Theorieseite 1 zusammengestellt. In dieser Aufgabe wird Bezug genommen auf
- das Kommutativ– und das Distributivgesetz,
- die neutralen Elemente von Addition und Multiplikation,
- die inversen Elemente von Addition und Multiplikation, sowie
- die Bestimmung primitiver Elemente.
Im vorliegenden Beispiel wäre $\beta$ ein primitives Element, wenn $\beta^2, \ \beta^3$ und $\beta^4$ (allgemein: $\beta^{q-1})$ die übrigen Elemente des Galoisfeldes $\rm GF(5)$ mit Ausnahme des Nullelementes ergeben.
Hinweis: Die Aufgabe bezieht ich auf das Themengebiet des Kapitels Einige Grundlagen der Algebra.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
