Aufgaben:Exercise 2.6Z: 4B3T Code according to Jessop and Waters

• Return to book

Code tables for the 4B3T code according to Jessop/Waters

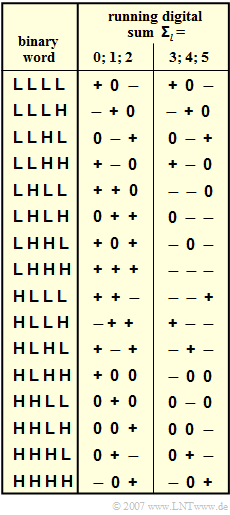
The graphic shows the two code tables for the 4B3T code according to Jessop and Waters. Depending on the current value of the running digital sum

$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.05cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu \hspace{0.05cm}$$

there are for each binary input tuple  $\rm LLLL$ ... $\rm \ HHHH$  two different ternary code sequences.

• In the table, "+" and "-" stand for the amplitude coefficients  $a_{\nu} = +1$  and  $a_{\nu} = –1$.
• The index  $l$  identifies the individual blocks.
• In the exercise, the following six input blocks are assumed:

$$\rm LLHL\hspace{0.1cm} HLLH \hspace{0.1cm}LHHH \hspace{0.1cm}HLLH \hspace{0.1cm}HLHH \hspace{0.1cm}HHLH.$$

• The running digital sum is initialized to  ${\it \Sigma}_{0} = 0$  in subtasks up to and including (2) or to  ${\it \Sigma}_{0} = 5$  in subtask (5).

Notes:

• The exercise belongs to the chapter  "Block Coding with 4B3T Codes".

• In this tutorial, the binary symbols are denoted by L ("Low") and H ("High"). Often you can find the binary symbols L and 0 (instead of H) in the literature. Sometimes, however, L corresponds to our H and 0 to L.
• To avoid such confusion and to prevent the "0" from appearing in both alphabets (binary and ternary) - in addition with different meanings - we have used the nomenclature which admittedly takes some getting used to. We are well aware that our nomenclature will also confuse some readers.
• You can check the results with the interaction module  "Principle of 4B3T coding". 

Questions

1

Code the input sequence $\rm LLHL\hspace{0.1cm} HLLH \hspace{0.1cm}LHHH \hspace{0.1cm}HLLH \hspace{0.1cm}HLHH \hspace{0.1cm}HHLH$ starting from the initial value  ${\it \Sigma}_{0} = 0$.
What is the ternary output sequence?

	$ \text{0 – +} \hspace{0.4cm} \text{– + +} \hspace{0.5cm} \text {– – –} \hspace{0.65cm} \text{– ++} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 +}\hspace{0.1cm}, $
	$ \text{0 – +} \hspace{0.4cm} \text{– + +} \hspace{0.4cm} \text{+ + +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– 0 0} \hspace{0.4cm} \text{0 0 +} \hspace{0.1cm},$
	$ \text{0 – +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– – –} \hspace{0.65cm} \text{– + +} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 –}\hspace{0.1cm}. $

2

What is the value of the running digital sum after coding the six blocks?

${\it \Sigma}_{6} \ = \ $

3

What is the maximum number of ternary values  $+1$  that can succeed each other?

$K_{+1} \ = \ $

4

What is the maximum number of ternary values  $0$  that can succeed each other?

$K_{0} \ = \ $

5

What is the value of the running digital sum after coding the six blocks, assuming  ${\it \Sigma}_{0} = 5$? 

${\it \Sigma}_{6} \ = \ $

Solution

Solution

1  The second solution is correct. The first ternary sequence would result with ${\it \Sigma}_{0} = 2$, the last with ${\it \Sigma}_{0} = 5$.

2  Starting from ${\it \Sigma}_{0} = 0$, the following values result for the running digital sum:

    ${\it \Sigma}_{1} = 0,$     ${\it \Sigma}_{2} = 1,$     ${\it \Sigma}_{3} = 4,$     ${\it \Sigma}_{4}= 3,$     ${\it \Sigma}_{5} = 2,$     ${\it \Sigma}_{6} \ \underline{= 3}.$

3  $K_{+1}\underline{ = 6}$ holds.   Also in the coded sequence of this exercise, one recognizes six consecutive plus signs coming from a total of three blocks:

• Two at the end of the second block,
• then three "$+1$" in block $3$ and
• finally one "$+1$" at the beginning of the fourth block.

Similarly, $K_{-1} = 6$ (see solution suggestion 3 in the first subtask).

4  If ${\it \Sigma}_{l} = 2$, the binary sequence $\rm HLHH\hspace{0.1cm} HHLH$ leads to the ternary sequence $+ 0 0 \hspace{0.1cm}0 0 –$. More than $K_{0}\ \underline{ = 4}$ consecutive zeros are not possible.

5  The ternary sequence here is:   $ \text{0 – +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– – –} \hspace{0.65cm} \text{– + +} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 –}\hspace{0.1cm}. $.

• The running digital sum builds up as follows:
  
  

    ${\it \Sigma}_{1} = 5,$     ${\it \Sigma}_{2} = 4,$     ${\it \Sigma}_{3} = 1,$     ${\it \Sigma}_{4}= 2,$     ${\it \Sigma}_{5} = 3,$     ${\it \Sigma}_{6} \ \underline{= 2}.$