Difference between revisions of "Aufgaben:Exercise 2.6Z: 4B3T Code according to Jessop and Waters"
| Line 70: | Line 70: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1''' The <u>second solution</u> is correct. The first ternary sequence would result with ${\it \Sigma}_{0} = 2$, the last with ${\it \Sigma}_{0} = 5$. | + | '''1''' The <u>second solution</u> is correct. |
| + | *The first ternary sequence would result with ${\it \Sigma}_{0} = 2$, | ||
| + | *the last with ${\it \Sigma}_{0} = 5$. | ||
| − | '''2''' Starting from ${\it \Sigma}_{0} = 0$, the following values result for the running digital sum:<br><br> | + | '''2''' Starting from ${\it \Sigma}_{0} = 0$, the following values result for the running digital sum:<br><br> |
${\it \Sigma}_{1} = 0,$ ${\it \Sigma}_{2} = 1,$ ${\it \Sigma}_{3} = 4,$ ${\it \Sigma}_{4}= 3,$ ${\it \Sigma}_{5} = 2,$ ${\it \Sigma}_{6} \ \underline{= 3}.$ | ${\it \Sigma}_{1} = 0,$ ${\it \Sigma}_{2} = 1,$ ${\it \Sigma}_{3} = 4,$ ${\it \Sigma}_{4}= 3,$ ${\it \Sigma}_{5} = 2,$ ${\it \Sigma}_{6} \ \underline{= 3}.$ | ||
| − | '''3''' $K_{+1}\underline{ = 6}$ holds. Also in the coded sequence of this exercise, one recognizes six consecutive plus signs coming from a total of three blocks: | + | '''3''' $K_{+1}\hspace{0.15cm}\underline{ = 6}$ holds. Also in the coded sequence of this exercise, |
| + | :$$ \text{0 – +} \hspace{0.4cm} \text{– + +} \hspace{0.4cm} \text{+ + +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– 0 0} \hspace{0.4cm} \text{0 0 +} \hspace{0.1cm},$$ | ||
| + | one recognizes six consecutive plus signs coming from a total of three blocks: | ||
*Two at the end of the second block, | *Two at the end of the second block, | ||
| − | *then three "$+1$" in block $3$ and | + | *then three "$+1$" in block $3$, and |
| − | *finally one "$+1$" at the beginning of the fourth block. | + | *finally one "$+1$" at the beginning of the fourth block. |
| − | Similarly, $K_{-1} = 6$ (see solution suggestion 3 in the first subtask). | + | Similarly, $K_{-1} = 6$ (see solution suggestion 3 in the first subtask). |
| − | '''4''' If ${\it \Sigma}_{l} = 2$, the binary sequence $\rm HLHH\hspace{0.1cm} HHLH$ leads to the ternary sequence $+ 0 0 \hspace{0.1cm}0 0 –$. More than $K_{0}\ \underline{ = 4}$ consecutive zeros are not possible. | + | '''4''' If ${\it \Sigma}_{l} = 2$, the binary sequence "$\rm HLHH\hspace{0.1cm} HHLH$" leads to the ternary sequence "$+ 0 0 \hspace{0.1cm}0 0 –$". |
| + | *More than $K_{0}\ \underline{ = 4}$ consecutive zeros are not possible. | ||
| − | '''5''' The ternary sequence here is: $ \text{0 – +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– – –} \hspace{0.65cm} \text{– + +} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 –} | + | '''5''' The ternary sequence here is: "$ \text{0 – +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– – –} \hspace{0.65cm} \text{– + +} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 –} $". |
| − | *The running digital sum builds up as follows: | + | *The running digital sum builds up as follows: ${\it \Sigma}_{1} = 5,$ ${\it \Sigma}_{2} = 4,$ ${\it \Sigma}_{3} = 1,$ ${\it \Sigma}_{4}= 2,$ ${\it \Sigma}_{5} = 3,$ ${\it \Sigma}_{6} \ \underline{= 2}.$ |
| − | |||
Latest revision as of 17:24, 19 May 2022
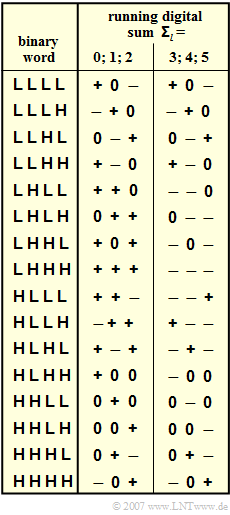
The graphic shows the two code tables for the 4B3T code according to Jessop and Waters.
Depending on the current value of the running digital sum
- $${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.05cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu \hspace{0.05cm}$$
there are for each binary input tuple $\rm LLLL$ ... $\rm \ HHHH$ two different ternary code sequences.
- In the table, "$+$" and "$-$" stand for the amplitude coefficients $a_{\nu} = +1$ and $a_{\nu} = -1$.
- The index $l$ identifies the individual blocks.
- In the exercise, the following six input blocks are assumed:
- $$\rm LLHL\hspace{0.1cm} HLLH \hspace{0.1cm}LHHH \hspace{0.1cm}HLLH \hspace{0.1cm}HLHH \hspace{0.1cm}HHLH.$$
- The running digital sum is initialized to ${\it \Sigma}_{0} = 0$ in subtasks up to and including (2) or to ${\it \Sigma}_{0} = 5$ in subtask (5).
Notes:
- The exercise belongs to the chapter "Block Coding with 4B3T Codes".
- The binary symbols are denoted by $\rm L$ ("Low") and $\rm H$ ("High") in this learning tutorial. Often you can find the binary symbols $\rm L$ and $\rm 0$ $($instead of $\rm H)$ in the literature. Sometimes, however, $\rm L$ corresponds to our $\rm H$ and $\rm 0$ to $\rm L$.
- To avoid such confusion and to prevent the $\rm 0$ from appearing in both alphabets (binary and ternary) - in addition with different meanings - we have used the nomenclature which admittedly takes some getting used to. We are well aware that our nomenclature will also confuse some readers.
- You can check the results with the (German language) SWF applet "Principle of 4B3T coding".
Questions
Solution
- The first ternary sequence would result with ${\it \Sigma}_{0} = 2$,
- the last with ${\it \Sigma}_{0} = 5$.
2 Starting from ${\it \Sigma}_{0} = 0$, the following values result for the running digital sum:
${\it \Sigma}_{1} = 0,$ ${\it \Sigma}_{2} = 1,$ ${\it \Sigma}_{3} = 4,$ ${\it \Sigma}_{4}= 3,$ ${\it \Sigma}_{5} = 2,$ ${\it \Sigma}_{6} \ \underline{= 3}.$
3 $K_{+1}\hspace{0.15cm}\underline{ = 6}$ holds. Also in the coded sequence of this exercise,
- $$ \text{0 – +} \hspace{0.4cm} \text{– + +} \hspace{0.4cm} \text{+ + +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– 0 0} \hspace{0.4cm} \text{0 0 +} \hspace{0.1cm},$$
one recognizes six consecutive plus signs coming from a total of three blocks:
- Two at the end of the second block,
- then three "$+1$" in block $3$, and
- finally one "$+1$" at the beginning of the fourth block.
Similarly, $K_{-1} = 6$ (see solution suggestion 3 in the first subtask).
4 If ${\it \Sigma}_{l} = 2$, the binary sequence "$\rm HLHH\hspace{0.1cm} HHLH$" leads to the ternary sequence "$+ 0 0 \hspace{0.1cm}0 0 –$".
- More than $K_{0}\ \underline{ = 4}$ consecutive zeros are not possible.
5 The ternary sequence here is: "$ \text{0 – +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– – –} \hspace{0.65cm} \text{– + +} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 –} $".
- The running digital sum builds up as follows: ${\it \Sigma}_{1} = 5,$ ${\it \Sigma}_{2} = 4,$ ${\it \Sigma}_{3} = 1,$ ${\it \Sigma}_{4}= 2,$ ${\it \Sigma}_{5} = 3,$ ${\it \Sigma}_{6} \ \underline{= 2}.$