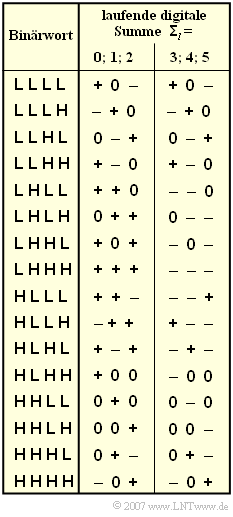
Exercise 2.6Z: 4B3T Code according to Jessop and Waters

Code tables for the 4B3T code according to Jessop/Waters

The graphic shows the two code tables for the 4B3T code according to Jessop and Waters. Depending on the current value of the running digital sum

$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.05cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu \hspace{0.05cm}$$

there are for each binary input tuple $\rm LLLL$ ... $\rm \ HHHH$ two different ternary code sequences.

In the table, "+" and "-" stand for the amplitude coefficients $a_{\nu} = +1$ and $a_{\nu} = –1$.
The index $l$ identifies the individual blocks.
In the exercise, the following six input blocks are assumed:

$$\rm LLHL\hspace{0.1cm} HLLH \hspace{0.1cm}LHHH \hspace{0.1cm}HLLH \hspace{0.1cm}HLHH \hspace{0.1cm}HHLH.$$

The running digital sum is initialized to ${\it \Sigma}_{0} = 0$ in subtasks up to and including (2) or to ${\it \Sigma}_{0} = 5$ in subtask (5).

Notes:

The exercise belongs to the chapter Block Coding with 4B3T Codes.

In this tutorial, the binary symbols are denoted by L ("Low") and H ("High"). Often you can find the binary symbols L and 0 (instead of H) in the literature. Sometimes, however, L corresponds to our H and 0 to L.
To avoid such confusion and to prevent the "0" from appearing in both alphabets (binary and ternary) - in addition with different meanings - we have used the nomenclature which admittedly takes some getting used to. We are well aware that our nomenclature will also confuse some readers.
You can check the results with the interaction module Principle of 4B3T coding.

Questions

	$ \text{0 – +} \hspace{0.4cm} \text{– + +} \hspace{0.5cm} \text {– – –} \hspace{0.65cm} \text{– ++} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 +}\hspace{0.1cm}, $
	$ \text{0 – +} \hspace{0.4cm} \text{– + +} \hspace{0.4cm} \text{+ + +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– 0 0} \hspace{0.4cm} \text{0 0 +} \hspace{0.1cm},$
	$ \text{0 – +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– – –} \hspace{0.65cm} \text{– + +} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 –}\hspace{0.1cm}. $

${\it \Sigma}_{6} \ = \ $

$K_{+1} \ = \ $

$K_{0} \ = \ $

${\it \Sigma}_{6} \ = \ $

Solution

1 The second solution is correct. The first ternary sequence would result with ${\it \Sigma}_{0} = 2$, the last with ${\it \Sigma}_{0} = 5$.

2 Starting from ${\it \Sigma}_{0} = 0$, the following values result for the running digital sum:

${\it \Sigma}_{1} = 0,$ ${\it \Sigma}_{2} = 1,$ ${\it \Sigma}_{3} = 4,$ ${\it \Sigma}_{4}= 3,$ ${\it \Sigma}_{5} = 2,$ ${\it \Sigma}_{6} \ \underline{= 3}.$

3 $K_{+1}\underline{ = 6}$ holds. Also in the coded sequence of this exercise, one recognizes six consecutive plus signs coming from a total of three blocks:

Two at the end of the second block,
then three "$+1$" in block $3$ and
finally one "$+1$" at the beginning of the fourth block.

Similarly, $K_{-1} = 6$ (see solution suggestion 3 in the first subtask).

4 If ${\it \Sigma}_{l} = 2$, the binary sequence $\rm HLHH\hspace{0.1cm} HHLH$ leads to the ternary sequence $+ 0 0 \hspace{0.1cm}0 0 –$. More than $K_{0}\ \underline{ = 4}$ consecutive zeros are not possible.

5 The ternary sequence here is: $ \text{0 – +} \hspace{0.4cm} \text{+ – –} \hspace{0.5cm} \text{– – –} \hspace{0.65cm} \text{– + +} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 –}\hspace{0.1cm}. $.

The running digital sum builds up as follows:

${\it \Sigma}_{1} = 5,$ ${\it \Sigma}_{2} = 4,$ ${\it \Sigma}_{3} = 1,$ ${\it \Sigma}_{4}= 2,$ ${\it \Sigma}_{5} = 3,$ ${\it \Sigma}_{6} \ \underline{= 2}.$