Aufgaben:Exercise 2.7Z: Power-Spectral Density of Pseudo-Ternary Codes

• Return to book

Power-spectral densities of
three different pseudo-ternary codes

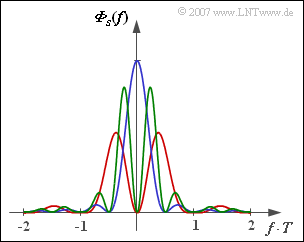
In the graph you can see the power-spectral densities  $\rm (PSD)$  of three different pseudo-ternary codes,  which result from the general description according to  "Exercise 2.7"  by different values of the parameters  $N_{\rm C}$  and  $K_{\rm C}$. 

In different colors the power-spectral densities

$${\it \Phi}_s(f) = \ \frac{s_0^2 \cdot T}{2} \cdot {\rm sinc}^2 (f T) \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ]$$

are shown for the following variants:

• AMI code  $(N_{\rm C} = 1,\ K_{\rm C} = +1)$,
• duobinary code  $(N_{\rm C} = 1,\ K_{\rm C} = -1)$,
• second order bipolar code $ (N_{\rm C} = 2,\ K_{\rm C} = +1)$.

The above PSD equation assumes the use of rectangular NRZ basic transmission pulses.

All pseudo-ternary codes considered here have the same probability distribution:

$${\rm Pr}\big[s(t) = 0\big]= {1}/{2},\hspace{0.2cm}{\rm Pr}\big[s(t) = +s_0\big]= {\rm Pr}\big[s(t) = -s_0\big]={1}/{4}\hspace{0.05cm}.$$

Notes:

• The exercise belongs to the chapter  "Symbolwise Coding with Pseudo-Ternary Codes".

• You can check the results with the  (German language)  SWF applet  "Signals, ACF and PSD of pseudo-ternary codes". 

Questions

1

Which curve belongs to the  AMI code?

	red,
	blue,
	green.

2

Which curve belongs to the  duobinary code?

	red,
	blue,
	green.

3

Which curve belongs to the  second order bipolar code?

	red,
	blue,
	green.

4

Which code has the highest transmit power?

	AMI code,
	duobinary code,
	2nd order bipolar code.
	The transmit power is the same for all codes.

5

Which of these codes has no DC component?

	AMI code,
	duobinary code,
	2nd order bipolar code.

6

Why do you need DC signal free codes for the  "telephone channel"?

	Transformers are needed to connect lines of different impedance.  These have high-pass character.
	Since power is often supplied via the signal line,  the message signal must not contain any DC signal components.

Solution

Solution

(1)  In AMI code, the PSD can be transformed as follows:

$${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$

This curve shape is shown in red. The PSD of the amplitude coefficients is ${\it \Phi}_{a}(f) = \sin^2(\pi fT)$.

(2)  After reshaping, we obtain for the duobinary code:

$${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \cos^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$

In the graph, the duobinary code is drawn in blue. Furthermore, ${\it \Phi}_{a}(f) = \cos^2(\pi fT)$.

(3)  The second order bipolar code differs from the AMI code only by the factor $2$ in the argument of the $\sin^{2}$ function:

$${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (2\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$

The green curve represents this function progression. Compared to AMI code, ${\it \Phi}_{a}(f)$ is exactly half as wide.

(4)  The transmit power $P_{\rm S}$ is equal to the integral over the power-spectral density ${\it \Phi}_{s}(f)$ and is the same for all codes considered here   ⇒   solution 4.

• This also follows from the power calculation by coulter averaging:

$$P_{\rm S} = \ {\rm Pr}[s(t) = +s_0] \cdot (+s_0)^2 + {\rm Pr}[s(t) = -s_0] \cdot (-s_0)^2= {1}/{4}\cdot s_0^2 + {1}/{4}\cdot s_0^2 = {1}/{2}\cdot s_0^2\hspace{0.05cm}.$$

(5)  Solutions 1 and 3 are correct:

• Equal signal freedom exists if the power-spectral density has no component at frequency $f = 0$.
• This is true for the AMI code and the second order bipolar code.
• This statement does not only mean that $s(t)$ has no DC component, i.e. that ${\it \Phi}_{s}(f)$ has no Dirac delta function at $f = 0$.
• Moreover, it also means that the continuous PSD component vanishes at $f = 0$.
• This is achieved exactly when both the long "$+1$" and the long "$–1$" sequences are excluded by the coding rule.

(6)  Both solutions apply in practice.