Difference between revisions of "Aufgaben:Exercise 2.7Z: Power-Spectral Density of Pseudo-Ternary Codes"
m (Text replacement - "Category:Aufgaben zu Digitalsignalübertragung" to "Category:Digital Signal Transmission: Exercises") |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Symbol-Wise_Coding_with_Pseudo_Ternary_Codes |
}} | }} | ||
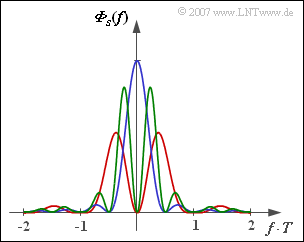
| − | [[File:P_ID1354__Dig_Z_2_7.png|right|frame| | + | [[File:P_ID1354__Dig_Z_2_7.png|right|frame|Power-spectral densities of three different pseudo ternary codes]] |
| − | In | + | In the graph you can see the power-spectral densities of three different pseudo ternary codes, which result from the general description according to [[Aufgaben:2.7_AMI-Code|Aufgabe 2.7]] by different values of the parameters $N_{\rm C}$ and $K_{\rm C}$. In different colors the power-spectral densities |
:$${\it \Phi}_s(f) 0 \ \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 (\pi f T) \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ]$$ | :$${\it \Phi}_s(f) 0 \ \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 (\pi f T) \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ]$$ | ||
| − | + | are shown for the following variants: | |
| − | * | + | *AMI code $(N_{\rm C} = 1, K_{\rm C} = +1)$, |
| − | * | + | *duobinary code $(N_{\rm C} = 1, K_{\rm C} = -1)$, |
| − | * | + | *second order bipolar code $ (N_{\rm C} = 2, K_{\rm C} = +1)$. |
| − | + | The above PSD equation assumes the use of rectangular NRZ basic transmission pulses. | |
| − | + | All pseudo ternary codes considered here have the same probability distribution: | |
:$${\rm Pr}\big[s(t) = 0\big]= {1}/{2},\hspace{0.2cm}{\rm Pr}\big[s(t) = +s_0\big]= {\rm Pr}\big[s(t) = -s_0\big]={1}/{4}\hspace{0.05cm}.$$ | :$${\rm Pr}\big[s(t) = 0\big]= {1}/{2},\hspace{0.2cm}{\rm Pr}\big[s(t) = +s_0\big]= {\rm Pr}\big[s(t) = -s_0\big]={1}/{4}\hspace{0.05cm}.$$ | ||
| Line 23: | Line 23: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Symbol-Wise_Coding_with_Pseudo_Ternary_Codes|Symbol-Wise Coding with Pseudo Ternary Codes]]. |
| − | * | + | *You can check the results with the interactive applet [[Applets:Pseudoternaercodierung|Signals, ACF and PSD of pseudo ternary codes]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which curve belongs to the '''AMI code'''? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + red, |
| − | - | + | - blue, |
| − | - | + | - green. |
| − | { | + | {Which curve belongs to the '''duobinary code'''? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - red, |
| − | + | + | + blue, |
| − | - | + | - green. |
| − | { | + | {Which curve belongs to the '''second order bipolar code'''? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - red, |
| − | - | + | - blue, |
| − | + | + | + green. |
| − | { | + | {Which code has the highest transmit power? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - AMI code, |
| − | - | + | - duobinary code, |
| − | - | + | - 2nd order bipolar code. |
| − | + | + | + The transmit power is the same for all codes. |
| − | { | + | {Which of these codes is equal-signal-free? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + AMI code, |
| − | - | + | - duobinary code, |
| − | + | + | + 2nd order bipolar code. |
| − | { | + | {Why do you need codes without equal signals for the "telephone channel"? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Transformers are needed to connect lines of different impedance. These have high-pass character. |
| − | + | + | + Since power is often supplied via the signal line, the message signal must not contain any DC signal components. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' In AMI code, the PSD can be transformed as follows: |
:$${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$ | :$${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$ | ||
| − | + | This curve shape is shown in <u>red</u>. The PSD of the amplitude coefficients is ${\it \Phi}_{a}(f) = \sin^2(\pi fT)$. | |
| − | '''(2)''' | + | '''(2)''' After reshaping, we obtain for the duobinary code: |
:$${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \cos^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$ | :$${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \cos^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$ | ||
| − | In | + | In the graph, the duobinary code is drawn in <u>blue</u>. Furthermore, ${\it \Phi}_{a}(f) = \cos^2(\pi fT)$. |
| − | '''(3)''' | + | '''(3)''' The second order bipolar code differs from the AMI code only by the factor $2$ in the argument of the $\sin^{2}$ function: |
:$${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (2\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$ | :$${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (2\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$ | ||
| − | + | The <u>green</u> curve represents this function progression. Compared to AMI code, ${\it \Phi}_{a}(f)$ is exactly half as wide. | |
| − | '''(4)''' | + | '''(4)''' The transmit power $P_{\rm S}$ is equal to the integral over the power-spectral density ${\it \Phi}_{s}(f)$ and is the same for all codes considered here ⇒ <u>solution 4</u>. |
| − | * | + | *This also follows from the power calculation by coulter averaging: |
:$$P_{\rm S} = \ {\rm Pr}[s(t) = +s_0] \cdot (+s_0)^2 + {\rm Pr}[s(t) = -s_0] \cdot (-s_0)^2= {1}/{4}\cdot s_0^2 + {1}/{4}\cdot s_0^2 = {1}/{2}\cdot s_0^2\hspace{0.05cm}.$$ | :$$P_{\rm S} = \ {\rm Pr}[s(t) = +s_0] \cdot (+s_0)^2 + {\rm Pr}[s(t) = -s_0] \cdot (-s_0)^2= {1}/{4}\cdot s_0^2 + {1}/{4}\cdot s_0^2 = {1}/{2}\cdot s_0^2\hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' <u>Solutions 1 and 3</u> are correct: |
| − | * | + | *Equal signal freedom exists if the power-spectral density has no component at frequency $f = 0$. |
| − | * | + | *This is true for the AMI code and the second order bipolar code. |
| − | * | + | *This statement does not only mean that $s(t)$ has no DC component, i.e. that ${\it \Phi}_{s}(f)$ has no Dirac delta function at $f = 0$. |
| − | * | + | *Moreover, it also means that the continuous PSD component vanishes at $f = 0$. |
| − | * | + | *This is achieved exactly when both the long "$+1$" and the long "$–1$" sequences are excluded by the coding rule. |
| − | '''(6)''' <u> | + | '''(6)''' <u>Both solutions</u> apply in practice. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 21:31, 22 April 2022
In the graph you can see the power-spectral densities of three different pseudo ternary codes, which result from the general description according to Aufgabe 2.7 by different values of the parameters $N_{\rm C}$ and $K_{\rm C}$. In different colors the power-spectral densities
- $${\it \Phi}_s(f) 0 \ \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 (\pi f T) \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ]$$
are shown for the following variants:
- AMI code $(N_{\rm C} = 1, K_{\rm C} = +1)$,
- duobinary code $(N_{\rm C} = 1, K_{\rm C} = -1)$,
- second order bipolar code $ (N_{\rm C} = 2, K_{\rm C} = +1)$.
The above PSD equation assumes the use of rectangular NRZ basic transmission pulses.
All pseudo ternary codes considered here have the same probability distribution:
- $${\rm Pr}\big[s(t) = 0\big]= {1}/{2},\hspace{0.2cm}{\rm Pr}\big[s(t) = +s_0\big]= {\rm Pr}\big[s(t) = -s_0\big]={1}/{4}\hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter Symbol-Wise Coding with Pseudo Ternary Codes.
- You can check the results with the interactive applet Signals, ACF and PSD of pseudo ternary codes.
Questions
Solution
- $${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$
This curve shape is shown in red. The PSD of the amplitude coefficients is ${\it \Phi}_{a}(f) = \sin^2(\pi fT)$.
(2) After reshaping, we obtain for the duobinary code:
- $${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \cos^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$
In the graph, the duobinary code is drawn in blue. Furthermore, ${\it \Phi}_{a}(f) = \cos^2(\pi fT)$.
(3) The second order bipolar code differs from the AMI code only by the factor $2$ in the argument of the $\sin^{2}$ function:
- $${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (2\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$
The green curve represents this function progression. Compared to AMI code, ${\it \Phi}_{a}(f)$ is exactly half as wide.
(4) The transmit power $P_{\rm S}$ is equal to the integral over the power-spectral density ${\it \Phi}_{s}(f)$ and is the same for all codes considered here ⇒ solution 4.
- This also follows from the power calculation by coulter averaging:
- $$P_{\rm S} = \ {\rm Pr}[s(t) = +s_0] \cdot (+s_0)^2 + {\rm Pr}[s(t) = -s_0] \cdot (-s_0)^2= {1}/{4}\cdot s_0^2 + {1}/{4}\cdot s_0^2 = {1}/{2}\cdot s_0^2\hspace{0.05cm}.$$
(5) Solutions 1 and 3 are correct:
- Equal signal freedom exists if the power-spectral density has no component at frequency $f = 0$.
- This is true for the AMI code and the second order bipolar code.
- This statement does not only mean that $s(t)$ has no DC component, i.e. that ${\it \Phi}_{s}(f)$ has no Dirac delta function at $f = 0$.
- Moreover, it also means that the continuous PSD component vanishes at $f = 0$.
- This is achieved exactly when both the long "$+1$" and the long "$–1$" sequences are excluded by the coding rule.
(6) Both solutions apply in practice.