Difference between revisions of "Aufgaben:Exercise 2.8: Code Comparison: Binary, AMI and 4B3T"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Symbolweise Codierung mit Pseudoternärcodes }} [[File:|right|]] ===Fragebogen=== <quiz display=simple…“) |
|||
| (25 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Symbolwise_Coding_with_Pseudo-Ternary_Codes |
}} | }} | ||
| − | [[File:|right|]] | + | [[File:EN_Dig_A_2_8.png|right|frame|Eye diagrams of different codes]] |
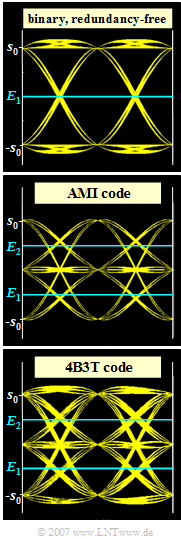
| + | In the graphic three eye diagrams (without noise) are shown, where in each case a rectangular NRZ basic transmission pulse and for the total system frequency response (of transmitter, channel and decoder, without encoder) a cosine rolloff characteristic with rolloff factor $r = 0.8$ are the basis. | ||
| + | For the individual eye diagrams it is furthermore assumed (from top to bottom): | ||
| + | *the redundancy-free binary code, | ||
| + | *the AMI code (approx. $37 \%$ redundancy), | ||
| + | *the 4B3T code (approx. $16 \%$ redundancy). | ||
| − | === | + | |
| + | Further, the following conditions can be assumed: | ||
| + | *AWGN noise is present, where holds: | ||
| + | :$$10 \cdot {\rm lg}\hspace{0.1cm} ({s_0^2 \cdot T}/{N_0}) = 10\, {\rm dB}\hspace{0.05cm}.$$ | ||
| + | *The detection noise power has the following value for the binary system (due to the non-optimal receiver filter $12 \%$ markup): | ||
| + | :$$\sigma_d^2 = 1.12 \cdot {N_0}/({2 T})\hspace{0.05cm}.$$ | ||
| + | *The symbol error probability of the binary system is: | ||
| + | :$$p_{\rm S} = {\rm Q} \left( {s_0}/{ \sigma_d} \right) \hspace{0.05cm}.$$ | ||
| + | *In contrast, for the two redundant pseudo-ternary systems: | ||
| + | :$$p_{\rm S} = {4}/{3} \cdot {\rm Q} \left( s_0/(2 \sigma_d) \right) \hspace{0.05cm}.$$ | ||
| + | *It should be taken into account that the noise rms value $\sigma_{d}$ may well change with respect to the redundancy-free binary system. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Symbolwise_Coding_with_Pseudo-Ternary_Codes|"Symbolwise Coding with Pseudo-Ternary Codes"]]. | ||
| + | |||
| + | *Reference is also made to the chapter [[Digital_Signal_Transmission/Blockweise_Codierung_mit_4B3T-Codes|"Block Coding with 4B3T Codes"]]. | ||
| + | |||
| + | *For numerical evaluation of the Q-function you can use the HTML5/JavaScript applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|"Complementary Gaussian Error Functions"]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| − | |type=" | + | {Calculate the (normalized) noise root mean square for the '''binary system'''. |
| − | - | + | |type="{}"} |
| − | + | $\sigma_{d}/s_{0} \ = \ $ { 0.237 3% } | |
| + | |||
| + | |||
| + | {What is the error probability of the binary system? | ||
| + | |type="{}"} | ||
| + | $\ p_{\rm S} \ = \ $ { 1.22 3% } $\ \cdot 10^{-5}$ | ||
| + | |||
| + | |||
| + | {What is the noise rms value for the system with '''AMI coding'''? | ||
| + | |type="{}"} | ||
| + | $\sigma_{d}/s_{0} \ = \ $ { 0.237 3% } | ||
| − | { | + | {What is the error probability with AMI coding? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\ p_{\rm S} \ = \ $ { 2.32 3% } $\ \%$ |
| + | |||
| + | {What is the noise rms value when using the '''4B3T code'''? | ||
| + | |type="{}"} | ||
| + | $\sigma_{d}/s_{0} \ = \ $ { 0.205 3% } | ||
| + | {What is the error probability of the 4B3T code? | ||
| + | |type="{}"} | ||
| + | $\ p_{\rm S} \ = \ $ { 1.11 3% } $\ \%$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' From the given S/N ratio, we obtain: |
| − | '''(2)''' | + | :$$10 \cdot {\rm lg}\hspace{0.1cm}({s_0^2 \cdot T}/{N_0}) = 10\, {\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{N_0} = { s_0^2 \cdot T}/{10}$$ |
| − | '''(3)''' | + | :$$ \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma_d^2 = 1.12 \cdot {N_0}/({2 T}) = 0.056 \cdot s_0^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{ \sigma_d}/{s_0} \hspace{0.15cm}\underline { = 0.237}\hspace{0.05cm}.$$ |
| − | '''(4)''' | + | |
| − | '''(5)''' | + | |
| − | '''( | + | '''(2)''' From this, it follows for the symbol error probability of the binary redundancy-free reference system: |
| + | :$$p_{\rm S} = {\rm Q} \left( {s_0}/{ \sigma_d} \right)\approx {\rm Q}(4.22)\hspace{0.15cm}\underline { = 1.22 \cdot 10^{-5}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' The symbol duration $T$ of the AMI encoded signal is equal to the bit duration $T_{\rm B}$ of the binary signal. | ||
| + | *Therefore, the bandwidth ratios do not change and the same noise rms value is obtained as calculated in point '''(1)''': | ||
| + | :$${ \sigma_d}/{s_0}\hspace{0.15cm}\underline { = 0.237} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' Due to the ternary decision, the argument of the Q-function is halved: | ||
| + | :$$p_{\rm S} \approx{4}/{3}\cdot {\rm Q}(2.11)={4}/{3} \cdot 1.74 \cdot 10^{-2}\hspace{0.15cm}\underline { = 2.32 \cdot 10^{-2}} \hspace{0.05cm}.$$ | ||
| + | *Here, the factor $4/3$ takes into account that the inner symbol $0$ can be falsified in two directions. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' When 4B3T coding is applied, the symbol rate is reduced by $25 \%$. | ||
| + | *By the same factor $0.75$, this makes the noise power smaller than calculated in '''(1)''' and '''(3)'''. From this follows: | ||
| + | :$${ \sigma_d}/{s_0} = \sqrt{0.75} \cdot 0.237 \hspace{0.15cm}\underline {\approx 0.205} \hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(6)''' Due to the smaller noise rms value, the error probability is now smaller than with the AMI code: | ||
| + | :$$p_{\rm S} \approx {4}/{3} \cdot {\rm Q} \left( \frac{0.5}{ 0.205} \right) = {4}/{3} \cdot 0.833 \cdot 10^{-2}\hspace{0.15cm}\underline { = 1.11 \cdot 10^{-2}} \hspace{0.05cm}.$$ | ||
| + | *But the 4B3T code cannot achieve the significantly smaller error probability of the redundancy-free binary code due to the ternary decision (half eye opening). | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^2.4 Pseudo-Ternary Codes^]] |
Latest revision as of 17:43, 25 May 2022
In the graphic three eye diagrams (without noise) are shown, where in each case a rectangular NRZ basic transmission pulse and for the total system frequency response (of transmitter, channel and decoder, without encoder) a cosine rolloff characteristic with rolloff factor $r = 0.8$ are the basis.
For the individual eye diagrams it is furthermore assumed (from top to bottom):
- the redundancy-free binary code,
- the AMI code (approx. $37 \%$ redundancy),
- the 4B3T code (approx. $16 \%$ redundancy).
Further, the following conditions can be assumed:
- AWGN noise is present, where holds:
- $$10 \cdot {\rm lg}\hspace{0.1cm} ({s_0^2 \cdot T}/{N_0}) = 10\, {\rm dB}\hspace{0.05cm}.$$
- The detection noise power has the following value for the binary system (due to the non-optimal receiver filter $12 \%$ markup):
- $$\sigma_d^2 = 1.12 \cdot {N_0}/({2 T})\hspace{0.05cm}.$$
- The symbol error probability of the binary system is:
- $$p_{\rm S} = {\rm Q} \left( {s_0}/{ \sigma_d} \right) \hspace{0.05cm}.$$
- In contrast, for the two redundant pseudo-ternary systems:
- $$p_{\rm S} = {4}/{3} \cdot {\rm Q} \left( s_0/(2 \sigma_d) \right) \hspace{0.05cm}.$$
- It should be taken into account that the noise rms value $\sigma_{d}$ may well change with respect to the redundancy-free binary system.
Notes:
- The exercise belongs to the chapter "Symbolwise Coding with Pseudo-Ternary Codes".
- Reference is also made to the chapter "Block Coding with 4B3T Codes".
- For numerical evaluation of the Q-function you can use the HTML5/JavaScript applet "Complementary Gaussian Error Functions".
Questions
Solution
- $$10 \cdot {\rm lg}\hspace{0.1cm}({s_0^2 \cdot T}/{N_0}) = 10\, {\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{N_0} = { s_0^2 \cdot T}/{10}$$
- $$ \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma_d^2 = 1.12 \cdot {N_0}/({2 T}) = 0.056 \cdot s_0^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{ \sigma_d}/{s_0} \hspace{0.15cm}\underline { = 0.237}\hspace{0.05cm}.$$
(2) From this, it follows for the symbol error probability of the binary redundancy-free reference system:
- $$p_{\rm S} = {\rm Q} \left( {s_0}/{ \sigma_d} \right)\approx {\rm Q}(4.22)\hspace{0.15cm}\underline { = 1.22 \cdot 10^{-5}} \hspace{0.05cm}.$$
(3) The symbol duration $T$ of the AMI encoded signal is equal to the bit duration $T_{\rm B}$ of the binary signal.
- Therefore, the bandwidth ratios do not change and the same noise rms value is obtained as calculated in point (1):
- $${ \sigma_d}/{s_0}\hspace{0.15cm}\underline { = 0.237} \hspace{0.05cm}.$$
(4) Due to the ternary decision, the argument of the Q-function is halved:
- $$p_{\rm S} \approx{4}/{3}\cdot {\rm Q}(2.11)={4}/{3} \cdot 1.74 \cdot 10^{-2}\hspace{0.15cm}\underline { = 2.32 \cdot 10^{-2}} \hspace{0.05cm}.$$
- Here, the factor $4/3$ takes into account that the inner symbol $0$ can be falsified in two directions.
(5) When 4B3T coding is applied, the symbol rate is reduced by $25 \%$.
- By the same factor $0.75$, this makes the noise power smaller than calculated in (1) and (3). From this follows:
- $${ \sigma_d}/{s_0} = \sqrt{0.75} \cdot 0.237 \hspace{0.15cm}\underline {\approx 0.205} \hspace{0.05cm}.$$
(6) Due to the smaller noise rms value, the error probability is now smaller than with the AMI code:
- $$p_{\rm S} \approx {4}/{3} \cdot {\rm Q} \left( \frac{0.5}{ 0.205} \right) = {4}/{3} \cdot 0.833 \cdot 10^{-2}\hspace{0.15cm}\underline { = 1.11 \cdot 10^{-2}} \hspace{0.05cm}.$$
- But the 4B3T code cannot achieve the significantly smaller error probability of the redundancy-free binary code due to the ternary decision (half eye opening).