Difference between revisions of "Aufgaben:Exercise 3.2: Eye Pattern according to Gaussian Low-Pass"
| (45 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Error_Probability_with_Intersymbol_Interference |
}} | }} | ||
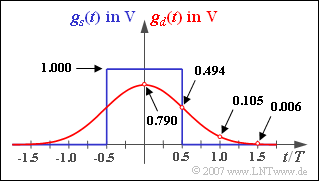
| − | [[File:P_ID1381__Dig_A_3_2.png|right|frame]] | + | [[File:P_ID1381__Dig_A_3_2.png|right|frame|Basic transmission pulse $g_s(t)$ ⇒ blue curve,<br>basic detection pulse $g_d(t)$ ⇒ red curve ]] |
| − | + | Let a binary bipolar redundancy-free baseband system with bit rate $R_{\rm B} = 100\,{\rm Mbit/s}$ be given. Further: | |
| − | * | + | * Rectangular transmission pulses, possible amplitude values $± 1\,{\rm V}$. |
| − | * | + | |
| − | * | + | * The AWGN noise power density $($on the resistor $1 \, \Omega)$: $N_0=10^{\rm -9} \, {\rm V}^2/{\rm Hz}$. |
| + | |||
| + | * Receiver filter is a Gaussian low-pass with cutoff frequency $f_{\rm G} = 50 \, {\rm MHz}$. The frequency response is: | ||
:$$H_{\rm G}(f) = {\rm e}^{- \pi \hspace{0.05cm}\cdot \hspace{0.05cm}{f}^2/({2f_{\rm G}})^2} | :$$H_{\rm G}(f) = {\rm e}^{- \pi \hspace{0.05cm}\cdot \hspace{0.05cm}{f}^2/({2f_{\rm G}})^2} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * The basic detection pulse $g_d(t) = g_s(t) * h_{\rm G}(t)$ is shown in the graph (red curve). <br>Some prominent pulse sample values are indicated. |
| − | * | + | |
| + | * The detection noise power can be calculated using the following equation: | ||
:$$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty} | :$$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty} | ||
|H_{\rm G}(f)|^2 \,{\rm d} f \hspace{0.05cm}.$$ | |H_{\rm G}(f)|^2 \,{\rm d} f \hspace{0.05cm}.$$ | ||
| − | + | The "eye diagram" can be used to determine the bit error probability $($in general: symbol error probability$)$. | |
| − | |||
| − | |||
| − | :$$ | ||
| − | |||
| − | + | # The mean symbol error probability $p_{\rm S}$ is obtained from this after averaging over all possible noiseless detection samples in consideration of the noise rms value $\sigma_d$. | |
| + | # The worst-case error probability serves as an upper bound for $p_{\rm S}$: | ||
| + | ::$$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} | ||
| + | \right) \hspace{0.3cm}{\rm with}\hspace{0.3cm}\frac{\ddot{o}(T_{\rm D})}{ 2}= g_d(t=0) - |g_d(t=T)|- |g_d(t=-T)|-\hspace{0.01cm}\text{ ...}$$ | ||
| − | + | ::Here, $\ddot{o}(T_{\rm D})$ denotes the vertical eye opening. Let the detection time $T_{\rm D} = 0$ be optimally chosen. | |
| − | |||
| − | === | + | |
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Error_Probability_with_Intersymbol_Interference|"Error Probability with Intersymbol Interference"]]. | ||
| + | |||
| + | * Use our HTML5/JavaScript applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|"Complementary Gaussian Error Functions"]] for the numerical evaluation of the Q–function. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the symbol duration? |
| − | |type=" | + | |type="{}"} |
| − | + | $T \ = \ $ { 10 3% } $\ {\rm ns}$ | |
| − | |||
| + | {What is the rms value of the detection noise signal? | ||
| + | |type="{}"} | ||
| + | $\sigma_d\ = \ $ { 0.188 3% } $\ {\rm V}$ | ||
| − | { | + | {What are the basic detection pulse samples $g_{\rm \nu} = g_d(\nu \cdot T)$, in particular |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $g_0\ = \ $ { 0.79 3% } $\ {\rm V}$ |
| + | $g_1\ = \ $ { 0.105 3% } $\ {\rm V}$ | ||
| + | $g_2\ = \ $ { 0 3% } $\ {\rm V}$ | ||
| + | {Calculate the eye opening and the worst-case error probability. | ||
| + | |type="{}"} | ||
| + | $\ddot{o}(T_{\rm D})\ = \ $ { 1.16 3% } $\ {\rm V}$ | ||
| + | $p_{\rm U}\ = \ $ { 1 3% } $\ \cdot 10^{\rm -3}$ | ||
| + | {Calculate the average error probability $p_{\rm S}$ by averaging over the possible noiseless samples. | ||
| + | |type="{}"} | ||
| + | $p_{\rm S}\ = \ $ { 0.256 3% } $\ \cdot 10^{\rm -3}$ | ||
| + | {What would be the minimum increase in transmitted pulse amplitude $s_0$ required to satisfy the condition $p_{\rm S} \ ≤ 10^{\rm -10}$? | ||
| + | |type="{}"} | ||
| + | $s_0\ = \ ${ 1.993 3% } $\ {\rm V}$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The symbol duration is the reciprocal of the bit rate: |
| − | '''(2)''' | + | :$$T = \frac{1}{10^8\,{\rm bit/s}} = 10^{-8}\,{\rm s}\hspace{0.15cm}\underline { = 10\,{\rm ns}} |
| − | '''(3)''' | + | \hspace{0.05cm}.$$ |
| − | '''(4)''' | + | |
| − | '''( | + | '''(2)''' Integration according to the given equation leads to: |
| − | + | :$$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} | |
| + | |H_{\rm G}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm | ||
| + | G}}{\sqrt{2}}= \frac{10^{-9}\,{\rm V/Hz} \cdot 5 \cdot | ||
| + | 10^{7}\,{\rm Hz} }{\sqrt{2}}\approx 0.035\,{\rm V^2}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}\sigma_d \hspace{0.15cm}\underline { = 0.188\,{\rm | ||
| + | V}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(3)''' These values can be obtained from the graph: | ||
| + | :$$g_0 = g_d(0)\hspace{0.15cm}\underline { = 0.790\,{\rm V}}, \hspace{0.2cm}g_1 = g_d(10\,{\rm | ||
| + | ns}) \hspace{0.15cm}\underline {= 0.105\,{\rm V}}= g_{-1}, \hspace{0.2cm}g_2 = g_{-2} \hspace{0.15cm}\underline { \approx | ||
| + | 0} \hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(4)''' Using the basic detection pulse values calculated in '''(3)''', we obtain for the vertical eye opening: | ||
| + | :$$\ddot{o}(T_{\rm D}) = 2 \cdot (g_0 - g_1 - g_{-1}) = 2 \cdot | ||
| + | (0.790\,{\rm V} - 2\cdot 0.105\,{\rm V}) \hspace{0.15cm}\underline {= 1.16\,{\rm | ||
| + | V}}\hspace{0.05cm}.$$ | ||
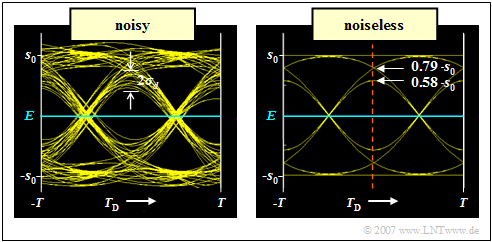
| + | [[File:EN_Dig_A_3_2_neu.png|right|frame|Eye diagram with and without noise]] | ||
| + | *The right graph shows the noisless eye diagram. One can see from this the vertical eye opening in the center of the symbol: | ||
| + | :$$\ddot{o}(T_{\rm D} = 0) = 2 \cdot 0.58 \cdot s_0.$$ | ||
| + | *Together with the noise rms value, we obtain for the worst-case error probability: | ||
| + | :$$p_{\rm U} = {\rm Q} \left( \frac{1.16\,{\rm | ||
| + | V}/2}{ 0.188\,{\rm V}} | ||
| + | \right) \approx {\rm Q}(3.08)\hspace{0.15cm}\underline {\approx 10^{-3}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(5)''' From the noisless eye diagram, one can see that the signal component at the detection time $T_{\rm D} = 0$ can assume six different values. | ||
| + | |||
| + | *In the upper half of the eye, these are: | ||
| + | :$$1.)\hspace{0.2cm} g_0 + g_1 + g_{-1} = 0.790\,{\rm V} + 2\cdot 0.105\,{\rm | ||
| + | V}= 1\,{\rm V} = s_0$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} | ||
| + | p_{\rm 1} = {\rm Q} \left( \frac{1\,{\rm | ||
| + | V}}{ 0.188\,{\rm V}} | ||
| + | \right) \approx 5 \cdot 10^{-8} | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$2.)\hspace{0.2cm} g_0 = 0.790\,{\rm V} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | p_{\rm 2} = {\rm Q} \left( \frac{0.790\,{\rm | ||
| + | V}}{ 0.188\,{\rm V}} | ||
| + | \right) \approx 1.3 \cdot 10^{-5} | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$3.)\hspace{0.2cm} g_0 - g_1 - g_{-1} = 0.580\,{\rm V} = \ddot{o}(T_{\rm | ||
| + | D})/2\hspace{0.3cm}\Rightarrow \hspace{0.3cm}p_{\rm 3} = p_{\rm U} \approx 10^{-3} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Averaging over these values with appropriate weighting $(p_2$ occurs twice as often as $p_1$ and $p_3)$ gives: | ||
| + | :$$p_{\rm S} \ = \ {1}/{4} \cdot (p_{\rm 1} + 2 \cdot p_{\rm 2} + p_{\rm 3}) | ||
| + | = {1}/{4} \cdot (5 \cdot 10^{-8} + 2 \cdot 1.3 \cdot 10^{-5} + 10^{-3}) | ||
| + | \hspace{0.15cm}\underline { \approx 0.256 \cdot 10^{-3}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | *Since $p_1$ and $p_2$ are much smaller than $p_3 = p_{\rm U}$, the average error probability is (almost) a factor of $4$ smaller than $p_{\rm U}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' To reduce the error probability, $s_0$ must be increased. Thus, the approximation $p_{\rm S} ≈ p_{\rm U}/4$ is even more accurate: | ||
| + | :$$p_{\rm S} \le 10^{-10}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}p_{\rm U} = {\rm Q} \left( \frac{0.58 \cdot s_0}{ 0.188\,{\rm V}} | ||
| + | \right)\le 4 \cdot 10^{-10}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} \frac{0.58 \cdot s_0}{ 0.188\,{\rm V}} | ||
| + | \ge 6.15 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}s_0 \ge 1.993\,{\rm V} \hspace{0.15cm}\underline { \approx 2\,{\rm V}} | ||
| + | \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^3.2 BER with Intersymbol Interference^]] |
Latest revision as of 16:36, 28 June 2022
Let a binary bipolar redundancy-free baseband system with bit rate $R_{\rm B} = 100\,{\rm Mbit/s}$ be given. Further:
- Rectangular transmission pulses, possible amplitude values $± 1\,{\rm V}$.
- The AWGN noise power density $($on the resistor $1 \, \Omega)$: $N_0=10^{\rm -9} \, {\rm V}^2/{\rm Hz}$.
- Receiver filter is a Gaussian low-pass with cutoff frequency $f_{\rm G} = 50 \, {\rm MHz}$. The frequency response is:
- $$H_{\rm G}(f) = {\rm e}^{- \pi \hspace{0.05cm}\cdot \hspace{0.05cm}{f}^2/({2f_{\rm G}})^2} \hspace{0.05cm}.$$
- The basic detection pulse $g_d(t) = g_s(t) * h_{\rm G}(t)$ is shown in the graph (red curve).
Some prominent pulse sample values are indicated.
- The detection noise power can be calculated using the following equation:
- $$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f \hspace{0.05cm}.$$
The "eye diagram" can be used to determine the bit error probability $($in general: symbol error probability$)$.
- The mean symbol error probability $p_{\rm S}$ is obtained from this after averaging over all possible noiseless detection samples in consideration of the noise rms value $\sigma_d$.
- The worst-case error probability serves as an upper bound for $p_{\rm S}$:
- $$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} \right) \hspace{0.3cm}{\rm with}\hspace{0.3cm}\frac{\ddot{o}(T_{\rm D})}{ 2}= g_d(t=0) - |g_d(t=T)|- |g_d(t=-T)|-\hspace{0.01cm}\text{ ...}$$
- Here, $\ddot{o}(T_{\rm D})$ denotes the vertical eye opening. Let the detection time $T_{\rm D} = 0$ be optimally chosen.
Notes:
- The exercise belongs to the chapter "Error Probability with Intersymbol Interference".
- Use our HTML5/JavaScript applet "Complementary Gaussian Error Functions" for the numerical evaluation of the Q–function.
Questions
Solution
- $$T = \frac{1}{10^8\,{\rm bit/s}} = 10^{-8}\,{\rm s}\hspace{0.15cm}\underline { = 10\,{\rm ns}} \hspace{0.05cm}.$$
(2) Integration according to the given equation leads to:
- $$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2}}= \frac{10^{-9}\,{\rm V/Hz} \cdot 5 \cdot 10^{7}\,{\rm Hz} }{\sqrt{2}}\approx 0.035\,{\rm V^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\sigma_d \hspace{0.15cm}\underline { = 0.188\,{\rm V}}\hspace{0.05cm}.$$
(3) These values can be obtained from the graph:
- $$g_0 = g_d(0)\hspace{0.15cm}\underline { = 0.790\,{\rm V}}, \hspace{0.2cm}g_1 = g_d(10\,{\rm ns}) \hspace{0.15cm}\underline {= 0.105\,{\rm V}}= g_{-1}, \hspace{0.2cm}g_2 = g_{-2} \hspace{0.15cm}\underline { \approx 0} \hspace{0.05cm}.$$
(4) Using the basic detection pulse values calculated in (3), we obtain for the vertical eye opening:
- $$\ddot{o}(T_{\rm D}) = 2 \cdot (g_0 - g_1 - g_{-1}) = 2 \cdot (0.790\,{\rm V} - 2\cdot 0.105\,{\rm V}) \hspace{0.15cm}\underline {= 1.16\,{\rm V}}\hspace{0.05cm}.$$
- The right graph shows the noisless eye diagram. One can see from this the vertical eye opening in the center of the symbol:
- $$\ddot{o}(T_{\rm D} = 0) = 2 \cdot 0.58 \cdot s_0.$$
- Together with the noise rms value, we obtain for the worst-case error probability:
- $$p_{\rm U} = {\rm Q} \left( \frac{1.16\,{\rm V}/2}{ 0.188\,{\rm V}} \right) \approx {\rm Q}(3.08)\hspace{0.15cm}\underline {\approx 10^{-3}} \hspace{0.05cm}.$$
(5) From the noisless eye diagram, one can see that the signal component at the detection time $T_{\rm D} = 0$ can assume six different values.
- In the upper half of the eye, these are:
- $$1.)\hspace{0.2cm} g_0 + g_1 + g_{-1} = 0.790\,{\rm V} + 2\cdot 0.105\,{\rm V}= 1\,{\rm V} = s_0$$
- $$\Rightarrow \hspace{0.3cm} p_{\rm 1} = {\rm Q} \left( \frac{1\,{\rm V}}{ 0.188\,{\rm V}} \right) \approx 5 \cdot 10^{-8} \hspace{0.05cm},$$
- $$2.)\hspace{0.2cm} g_0 = 0.790\,{\rm V} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm 2} = {\rm Q} \left( \frac{0.790\,{\rm V}}{ 0.188\,{\rm V}} \right) \approx 1.3 \cdot 10^{-5} \hspace{0.05cm},$$
- $$3.)\hspace{0.2cm} g_0 - g_1 - g_{-1} = 0.580\,{\rm V} = \ddot{o}(T_{\rm D})/2\hspace{0.3cm}\Rightarrow \hspace{0.3cm}p_{\rm 3} = p_{\rm U} \approx 10^{-3} \hspace{0.05cm}.$$
- Averaging over these values with appropriate weighting $(p_2$ occurs twice as often as $p_1$ and $p_3)$ gives:
- $$p_{\rm S} \ = \ {1}/{4} \cdot (p_{\rm 1} + 2 \cdot p_{\rm 2} + p_{\rm 3}) = {1}/{4} \cdot (5 \cdot 10^{-8} + 2 \cdot 1.3 \cdot 10^{-5} + 10^{-3}) \hspace{0.15cm}\underline { \approx 0.256 \cdot 10^{-3}} \hspace{0.05cm}.$$
- Since $p_1$ and $p_2$ are much smaller than $p_3 = p_{\rm U}$, the average error probability is (almost) a factor of $4$ smaller than $p_{\rm U}$.
(6) To reduce the error probability, $s_0$ must be increased. Thus, the approximation $p_{\rm S} ≈ p_{\rm U}/4$ is even more accurate:
- $$p_{\rm S} \le 10^{-10}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}p_{\rm U} = {\rm Q} \left( \frac{0.58 \cdot s_0}{ 0.188\,{\rm V}} \right)\le 4 \cdot 10^{-10}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{0.58 \cdot s_0}{ 0.188\,{\rm V}} \ge 6.15 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}s_0 \ge 1.993\,{\rm V} \hspace{0.15cm}\underline { \approx 2\,{\rm V}} \hspace{0.05cm}.$$