Difference between revisions of "Aufgaben:Exercise 3.4: Systematic Convolution Codes"
From LNTwww
m (Text replacement - "Category:Aufgaben zu Kanalcodierung" to "Category:Channel Coding: Exercises") |
|||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Algebraic_and_Polynomial_Description}} |
| − | [[File: | + | [[File:EN_KC_A_3_4.png|right|frame|Predefined filter structures]] |
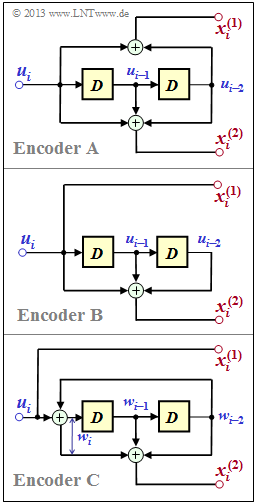
| − | + | One speaks of a "systematic convolutional code" of rate $R = 1/2$ ⇒ $k = 1, \ n = 2$, if the code bit $x_i^{(1)}$ is equal to the currently applied information bit $u_i$. | |
| − | + | *The transfer function matrix of such a code is: | |
:$${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) | :$${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *The encoder $\rm A$ shown in the upper graph is certainly not systematic, since for this $G^{(1)}(D) ≠ 1$ holds. To derive the matrix $\mathbf{G}(D)$ we refer to an [[Channel_Coding/Algebraic_and_Polynomial_Description#Application_of_the_D-transform_to_rate-1. 2Fn-convolution_encoders|$\text{earlier example}$]], where for our standard rate–1/2 encoder with memory $m = 2$ the transfer function matrix was determined: | |
:$${\boldsymbol{\rm G}}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big ( \hspace{0.05cm} G^{(1)}(D)\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) = \big ( \hspace{0.05cm} 1 + D + D^2\hspace{0.05cm} , \hspace{0.2cm} 1 + D^2 \hspace{0.05cm}\big ) | :$${\boldsymbol{\rm G}}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big ( \hspace{0.05cm} G^{(1)}(D)\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) = \big ( \hspace{0.05cm} 1 + D + D^2\hspace{0.05cm} , \hspace{0.2cm} 1 + D^2 \hspace{0.05cm}\big ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | :The encoder $\rm A$ differs from this example only by swapping the two outputs. | |
| − | * | + | *If the transfer function matrix of a code is |
:$${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} G^{(1)}(D)\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) | :$${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} G^{(1)}(D)\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | + | :then the equivalent systematic representation of this rate–1/2 convolutional code holds in general: | |
:$${\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} {G^{(2)}(D)}/{G^{(1)}(D)} \hspace{0.05cm}\big ) | :$${\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} {G^{(2)}(D)}/{G^{(1)}(D)} \hspace{0.05cm}\big ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In | + | In subtask '''(3)''', check which of the systematic arrangements is equivalent to encoder $\rm A$? |
| − | * | + | *Either encoder $\rm B$, |
| − | |||
| − | |||
| + | *or encoder $\rm C$ | ||
| + | |||
| + | *or both. | ||
| Line 33: | Line 34: | ||
| + | Hints: | ||
| + | * This exercise belongs to the chapter [[Channel_Coding/Algebraic_and_Polynomial_Description| "Algebraic and Polynomial Description"]]. | ||
| − | + | * Reference is made in particular to the sections | |
| − | * | + | :* [[Channel_Coding/Algebraic_and_Polynomial_Description#Transfer_Function_Matrix|"Transfer Function Matrix"]] and |
| − | * | + | :* [[Channel_Coding/Algebraic_and_Polynomial_Description#Equivalent_systematic_convolutional_code|"Equivalent systematic convolutional code"]]. |
| − | |||
| − | : | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the transfer function matrix of $\rm A$? |
|type="()"} | |type="()"} | ||
+ $\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$, | + $\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$, | ||
| Line 50: | Line 51: | ||
- $\mathbf{G}(D) = (1, \ 1 + D + D^2)$. | - $\mathbf{G}(D) = (1, \ 1 + D + D^2)$. | ||
| − | { | + | {What is the equivalent systematic transfer function matrix? |
|type="()"} | |type="()"} | ||
- $\mathbf{G}_{\rm sys}(D) = (1 + D + D^2, \ 1 + D^2)$, | - $\mathbf{G}_{\rm sys}(D) = (1 + D + D^2, \ 1 + D^2)$, | ||
| Line 56: | Line 57: | ||
+ $\mathbf{G}_{\rm sys}(D) = (1, \ (1 + D + D^2)/(1 + D^2))$. | + $\mathbf{G}_{\rm sys}(D) = (1, \ (1 + D + D^2)/(1 + D^2))$. | ||
| − | { | + | {Which encoder is equivalent to $\rm A$ and systematic? |
| − | |type=" | + | |type="[]"} |
| − | - | + | - Encoder $\rm B$ , |
| − | + | + | + encoder $\rm C$ . |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is the <u>proposed solution 1</u>: |
| − | * | + | *Proposition 2 would result if the two outputs were swapped, that is, for the [[Channel_Coding/Algebraic_and_Polynomial_Description#Application_of_the_D-transform_to_rate-1.2Fn-convolution_encoders|"rate–1/2 standard code"]] mostly considered in the theory section. |
| − | * | + | *Proposition 3 applies to a systematic code ⇒ $\underline{x}^{(1)} = \underline{u}$. However, the coder $\rm A$ considered here does not exhibit this property. |
| − | '''(2)''' | + | '''(2)''' To go from a nonsystematic $(n, \ k)$ code with matrix $\mathbf{G}(D)$ to the equivalent systematic code ⇒ matrix $\mathbf{G}_{\rm sys}(D)$, one must generally split $\mathbf{G}(D)$ into a $k × k$ matrix $\mathbf{T}(D)$ and a remainder matrix $\mathbf{Q}(D)$. |
| − | * | + | *The desired result is then with the $k × k$ identity matrix $\mathbf{I}_k$: |
:$${\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D)\hspace{0.05cm}\big ) | :$${\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D)\hspace{0.05cm}\big ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *We assume here the $\mathbf{G}(D)$ matrix for the coder $\rm A$. Because of $k = 1$ here both $\mathbf{T}(D)$ and $\mathbf{Q}(D)$ have dimension $1 × 1$, so strictly speaking they are not matrices at all: |
| − | |||
:$${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} {\boldsymbol{\rm T}}(D)\hspace{0.05cm} ; \hspace{0.2cm} {\boldsymbol{\rm Q}}(D)\hspace{0.05cm}\big ) | :$${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} {\boldsymbol{\rm T}}(D)\hspace{0.05cm} ; \hspace{0.2cm} {\boldsymbol{\rm Q}}(D)\hspace{0.05cm}\big ) | ||
\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\boldsymbol{\rm T}}(D) = \big ( 1+D^2\big )\hspace{0.05cm} , \hspace{0.2cm} | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\boldsymbol{\rm T}}(D) = \big ( 1+D^2\big )\hspace{0.05cm} , \hspace{0.2cm} | ||
{\boldsymbol{\rm Q}}(D) = \big ( 1+D+D^2\big )\hspace{0.05cm} .$$ | {\boldsymbol{\rm Q}}(D) = \big ( 1+D+D^2\big )\hspace{0.05cm} .$$ | ||
| − | * | + | *For the two elements of the systematic transfer function matrix, we obtain: |
:$$G^{(1)}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\boldsymbol{\rm T}}(D) \cdot {\boldsymbol{\rm T}}^{-1}(D) = 1 C,\hspace{0.8cm} | :$$G^{(1)}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\boldsymbol{\rm T}}(D) \cdot {\boldsymbol{\rm T}}^{-1}(D) = 1 C,\hspace{0.8cm} | ||
G^{(2)}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\boldsymbol{\rm Q}}(D) \cdot {\boldsymbol{\rm T}}^{-1}(D) = \frac{1+D+D^2}{1+D^2}$$ | G^{(2)}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\boldsymbol{\rm Q}}(D) \cdot {\boldsymbol{\rm T}}^{-1}(D) = \frac{1+D+D^2}{1+D^2}$$ | ||
| Line 89: | Line 89: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | So the <u>last proposed solution</u> is correct: | |
| − | * | + | *Proposed solution 1 does not describe a systematic code. |
| − | * | + | |
| + | *A code according to solution suggestion 2 is systematic, but not equivalent to the coder $\rm A$ according to the given circuit and transfer function matrix $\mathbf{G}(D)$. | ||
| − | '''(3)''' | + | '''(3)''' The generator function matrix of encoder $\rm B$ is: |
:$${\boldsymbol{\rm G}}_{\rm B}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} {1+D+D^2} \hspace{0.05cm}\big ) | :$${\boldsymbol{\rm G}}_{\rm B}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} {1+D+D^2} \hspace{0.05cm}\big ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *So this encoder is not equivalent to encoder $\rm A$. |
| − | * | + | |
| + | *Let us now consider the encoder $\rm C$. Here the second matrix element of $\mathbf{G}(D)$: | ||
:$$w_i \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_i + w_{i-2} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} | :$$w_i \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_i + w_{i-2} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} | ||
{U}(D) = W(D) \cdot (1 + D^2 ) \hspace{0.05cm},\hspace{0.8cm} | {U}(D) = W(D) \cdot (1 + D^2 ) \hspace{0.05cm},\hspace{0.8cm} | ||
| Line 106: | Line 108: | ||
:$$\Rightarrow \hspace{0.3cm} G^{(2)}(D) = \frac{{X}^{(2)}(D)}{{U}(D)} = \frac{1+D+D^2}{1+D^2}\hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} G^{(2)}(D) = \frac{{X}^{(2)}(D)}{{U}(D)} = \frac{1+D+D^2}{1+D^2}\hspace{0.05cm}.$$ | ||
| − | + | *This corresponds exactly to the result of subtask '''(2)''' ⇒ <u>Proposed solution 2</u>. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Channel Coding: Exercises|^3.2 | + | [[Category:Channel Coding: Exercises|^3.2 Polynomial Description^]] |
Latest revision as of 19:34, 10 November 2022
One speaks of a "systematic convolutional code" of rate $R = 1/2$ ⇒ $k = 1, \ n = 2$, if the code bit $x_i^{(1)}$ is equal to the currently applied information bit $u_i$.
- The transfer function matrix of such a code is:
- $${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) \hspace{0.05cm}.$$
- The encoder $\rm A$ shown in the upper graph is certainly not systematic, since for this $G^{(1)}(D) ≠ 1$ holds. To derive the matrix $\mathbf{G}(D)$ we refer to an $\text{earlier example}$, where for our standard rate–1/2 encoder with memory $m = 2$ the transfer function matrix was determined:
- $${\boldsymbol{\rm G}}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big ( \hspace{0.05cm} G^{(1)}(D)\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) = \big ( \hspace{0.05cm} 1 + D + D^2\hspace{0.05cm} , \hspace{0.2cm} 1 + D^2 \hspace{0.05cm}\big ) \hspace{0.05cm}.$$
- The encoder $\rm A$ differs from this example only by swapping the two outputs.
- If the transfer function matrix of a code is
- $${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} G^{(1)}(D)\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) \hspace{0.05cm},$$
- then the equivalent systematic representation of this rate–1/2 convolutional code holds in general:
- $${\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} {G^{(2)}(D)}/{G^{(1)}(D)} \hspace{0.05cm}\big ) \hspace{0.05cm}.$$
In subtask (3), check which of the systematic arrangements is equivalent to encoder $\rm A$?
- Either encoder $\rm B$,
- or encoder $\rm C$
- or both.
Hints:
- This exercise belongs to the chapter "Algebraic and Polynomial Description".
- Reference is made in particular to the sections
Questions
Solution
(1) Correct is the proposed solution 1:
- Proposition 2 would result if the two outputs were swapped, that is, for the "rate–1/2 standard code" mostly considered in the theory section.
- Proposition 3 applies to a systematic code ⇒ $\underline{x}^{(1)} = \underline{u}$. However, the coder $\rm A$ considered here does not exhibit this property.
(2) To go from a nonsystematic $(n, \ k)$ code with matrix $\mathbf{G}(D)$ to the equivalent systematic code ⇒ matrix $\mathbf{G}_{\rm sys}(D)$, one must generally split $\mathbf{G}(D)$ into a $k × k$ matrix $\mathbf{T}(D)$ and a remainder matrix $\mathbf{Q}(D)$.
- The desired result is then with the $k × k$ identity matrix $\mathbf{I}_k$:
- $${\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D)\hspace{0.05cm}\big ) \hspace{0.05cm}.$$
- We assume here the $\mathbf{G}(D)$ matrix for the coder $\rm A$. Because of $k = 1$ here both $\mathbf{T}(D)$ and $\mathbf{Q}(D)$ have dimension $1 × 1$, so strictly speaking they are not matrices at all:
- $${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} {\boldsymbol{\rm T}}(D)\hspace{0.05cm} ; \hspace{0.2cm} {\boldsymbol{\rm Q}}(D)\hspace{0.05cm}\big ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\boldsymbol{\rm T}}(D) = \big ( 1+D^2\big )\hspace{0.05cm} , \hspace{0.2cm} {\boldsymbol{\rm Q}}(D) = \big ( 1+D+D^2\big )\hspace{0.05cm} .$$
- For the two elements of the systematic transfer function matrix, we obtain:
- $$G^{(1)}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\boldsymbol{\rm T}}(D) \cdot {\boldsymbol{\rm T}}^{-1}(D) = 1 C,\hspace{0.8cm} G^{(2)}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\boldsymbol{\rm Q}}(D) \cdot {\boldsymbol{\rm T}}^{-1}(D) = \frac{1+D+D^2}{1+D^2}$$
- $$\Rightarrow \hspace{0.3cm}{\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.1cm} \frac{1+D+D^2}{1+D^2} \hspace{0.05cm}\big ) \hspace{0.05cm}.$$
So the last proposed solution is correct:
- Proposed solution 1 does not describe a systematic code.
- A code according to solution suggestion 2 is systematic, but not equivalent to the coder $\rm A$ according to the given circuit and transfer function matrix $\mathbf{G}(D)$.
(3) The generator function matrix of encoder $\rm B$ is:
- $${\boldsymbol{\rm G}}_{\rm B}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} {1+D+D^2} \hspace{0.05cm}\big ) \hspace{0.05cm}.$$
- So this encoder is not equivalent to encoder $\rm A$.
- Let us now consider the encoder $\rm C$. Here the second matrix element of $\mathbf{G}(D)$:
- $$w_i \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_i + w_{i-2} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {U}(D) = W(D) \cdot (1 + D^2 ) \hspace{0.05cm},\hspace{0.8cm} x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} w_i + w_{i-1} + w_{i-2} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {X}^{(2)}(D) = W(D) \cdot (1 +D + D^2 )$$
- $$\Rightarrow \hspace{0.3cm} G^{(2)}(D) = \frac{{X}^{(2)}(D)}{{U}(D)} = \frac{1+D+D^2}{1+D^2}\hspace{0.05cm}.$$
- This corresponds exactly to the result of subtask (2) ⇒ Proposed solution 2.