Exercise 3.4Z: Eye Opening and Level Number
In this exercise, a redundancy-free binary system and a redundancy-free quaternary system are compared with respect to vertical eye opening. The same boundary conditions apply to the two transmission systems:
- The basic transmission pulse $g_s(t)$ is NRZ rectangular in each case and has the height $s_0 = 1 \, {\rm V}$.
- The (equivalent) bit rate is $R_{\rm B} = 100 \, {\rm Mbit/s}$.
- The AWGN noise has the noise power density $N_0$.
- Let the receiver filter be a Gaussian low-pass filter with cutoff frequency $f_{\rm G} = 30 \, {\rm MHz}$:
- $$H_{\rm G}(f) = {\rm e}^{{- \pi \cdot f^2}/{(2f_{\rm G})^2}}\hspace{0.05cm}.$$
- The decision thresholds are optimal. The detection time is $T_{\rm D} = 0$.
For the half-eye opening of an M-level transmission system, the following holds in general:
- $${\ddot{o}(T_{\rm D})}/{ 2} = \frac{g_0}{ M-1} - \sum_{\nu = 1}^{\infty} |g_\nu | - \sum_{\nu = 1}^{\infty} |g_{-\nu} |\hspace{0.05cm}.$$
Here, $g_0 = g_d(t = 0)$ is the main value of the basic transmitter pulse $g_d(t) = g_s(t) * h_{\rm G}(t)$. The second term describes the trailer $g_{\rm \nu} = g_d(t = \nu T)$ and the last term the precursor $g_{\rm -\nu} = g_d(t = -\nu T)$.
Note that in the present configuration with Gaussian low-pass
- all the basic transmitter pulse values $\text{...} \, g_{\rm -1}, \, g_0, \, g_1, \, \text{...}$ are positive,
- the (infinite) sum $\text{...} \, + \, g_{\rm -1} + g_0 + g_1\,\text{...}$ gives the constant value $s_0$,
- the main value can be calculated with the complementary Gaussian error function ${\rm Q}(x)$:
- $$g_0 = s_0 \cdot\big [ 1- 2 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\big] \hspace{0.05cm}.$$
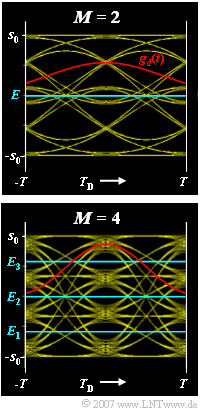
The graph shows the eye diagrams of the binary and quaternary systems and, in red, the corresponding basic transmitter pulses $g_d(t)$:
- The optimal decision thresholds $E$ $($for $M = 2)$ and $E_1$, $E_2$, $E_3$ $($for $M = 4)$ are also drawn.
- In subtask (7) these are to be determined numerically.
Notes:
- The exercise belongs to the chapter Intersymbol Interference for Multi-Level Transmission.
- For the complementary Gaussian error function applies:
- $${\rm Q}(0.25) = 0.4013,\hspace{0.2cm}{\rm Q}(0.50) = 0.3085,\hspace{0.2cm}{\rm Q}(0.75) = 0.2266,\hspace{0.2cm}{\rm Q}(1.00) = 0.1587,$$
- $${\rm Q}(1.25) = 0.1057,\hspace{0.2cm}{\rm Q}(1.50) = 0.0668,\hspace{0.2cm}{\rm Q}(1.75) = 0.0401,\hspace{0.2cm}{\rm Q}(2.00) = 0.0228.$$
Questions
Solution
- $$T = \frac{1}{R_{\rm B}}= \frac{1}{100\,{\rm Mbit/s}}\hspace{0.15cm}\underline {= 10\,{\rm ns}}\hspace{0.05cm}.$$
The symbol duration of the quaternary system is twice as large:
- $$T = \frac{{\rm log_2}\hspace{0.1cm}4}{R_{\rm B}}\hspace{0.15cm}\underline {= 20\,{\rm ns}}\hspace{0.05cm}.$$
(2) According to the given equation, the following holds for the binary system:
- $$g_0 \ = \ s_0 \cdot\left [ 1- 2 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right]= 1\,{\rm V} \cdot\left [ 1- 2 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot 30\,{\rm MHz} \cdot 10\,{\rm ns} \right)\right] $$
- $$\Rightarrow \hspace{0.3cm} g_0 \ \approx \ 1\,{\rm V} \cdot\left [ 1- 2 \cdot {\rm Q} \left( 0.75 \right)\right] = 1\,{\rm V} \cdot\left [ 1- 2 \cdot 0.2266 \right]\hspace{0.15cm}\underline { = 0.547\,{\rm V}} \hspace{0.05cm}.$$
(3) Due to the double symbol duration, the same cutoff frequency for $M = 4$:
- $$g_0 \ = 1\,{\rm V} \cdot\left [ 1- 2 \cdot {\rm Q} \left( 1.5 \right)\right] = 1\,{\rm V} \cdot\left [ 1- 2 \cdot 0.0668 \right] \hspace{0.15cm}\underline {= 0.867\,{\rm V}} \hspace{0.05cm}.$$
(4) Extending the given equation by $±g_0$, we obtain:
- $${\ddot{o}(T_{\rm D})}/{ 2} = \frac{g_0}{ M-1} + g_0 - g_0 - \sum_{\nu = 1}^{\infty} g_\nu - \sum_{\nu = 1}^{\infty} g_{-\nu} = \frac{M}{ M-1} \cdot g_0 - s_0 \hspace{0.05cm}.$$
Here is taken into account:
- In the case of the Gaussian low-pass filter, the magnitude formation can be omitted.
- The sum over all detection pulse values is equal to $s_0$.
The first, but also the last solution is correct:
- $${\ddot{o}(T_{\rm D})}/{ 2} \ = \ \frac{M}{ M-1} \cdot g_0 - s_0 = \frac{M}{ M-1} \cdot s_0 \cdot\left [ 1- 2 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right]- s_0 $$
- $$\Rightarrow \hspace{0.3cm} {\ddot{o}(T_{\rm D})}/{ 2} \ = \ \frac{s_0}{ M-1} \cdot \left [ 1- 2 \cdot M \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right] \hspace{0.05cm}.$$
Using the relation $T = {\rm log_2} \,(M)/R_{\rm B}$, we arrive at the third proposed solution, which is also applicable.
(5) Using the results from (2) and (4) and $M = 2$, one obtains:
- $${\ddot{o}(T_{\rm D})} = 2 \cdot (2 \cdot g_0 - s_0) = 2 \cdot (2 \cdot 0.547\,{\rm V} - 1\,{\rm V}) \hspace{0.15cm}\underline {= 0.188\,{\rm V}} \hspace{0.05cm}.$$
(6) On the other hand, with $g_0 = 0.867 \, {\rm V}$, $s_0 = 1 \, {\rm V}$ and $M = 4$, we get:
- $${\ddot{o}(T_{\rm D})} = 2 \cdot ({4}/{3} \cdot 0.867\,{\rm V} - 1\,{\rm V}) \hspace{0.15cm}\underline {= 0.312\,{\rm V}} \hspace{0.05cm}.$$
(7) According to subtask (3), $g_0 = 0.867 \, {\rm V}$ and correspondingly $g_{\rm VN} = 0.133 \, {\rm V}$ (sum of all precursors and trailers).
- The eye opening is $\ddot{o} = 0.312 \, {\rm V}$.
- From the sketch on the information section, we can see that the upper boundary of the upper eye has the following value (for $T_{\rm D} = 0$):
- $$o = s_0 - 2 \cdot g_{\rm VN}= g_0 - g_{\rm VN}= 0.867\,{\rm V} - 0.133\,{\rm V} = 0.734\,{\rm V} \hspace{0.05cm}.$$
- The lower limit is at:
- $$u = o -{\ddot{o}} = 0.734\,{\rm V} - 0.312\,{\rm V} = 0.422\,{\rm V} \hspace{0.05cm}.$$
- From this follows for the optimal decision threshold of the upper eye:
- $$E_3 = \frac{o + u}{2} = \frac{0.734\,{\rm V} + 0.422\,{\rm V}}{2} { = 0.578\,{\rm V}} \hspace{0.05cm}.$$
- The sought threshold (for the lower eye) is $E_1 \, \underline {= \, –0.578 \, V}$.
- The average decision threshold is $E_2 = 0$ for symmetry reasons.