Difference between revisions of "Aufgaben:Exercise 4.12Z: 4-QAM Systems again"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Quadratur–Amplitudenmodulation }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice…“) |
|||
| (33 intermediate revisions by 5 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
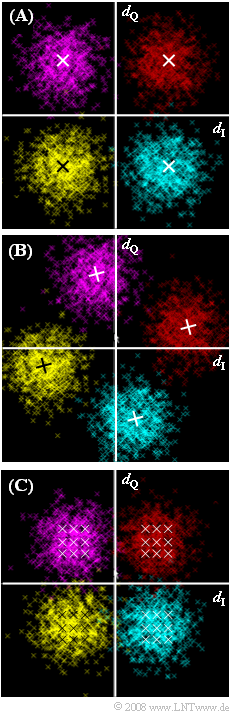
| − | [[File:|right|]] | + | [[File:P_ID1724__Mod_Z_4_11.png|right|frame|Phase diagrams for 4–QAM, ideal and with degradations]] |
| + | Graph $\rm (A)$ shows the phase diagram of the 4-QAM after the matched filter, where an optimal realization form was chosen in the case of AWGN noise under the constraint of "peak limiting": | ||
| + | * rectangular basic transmision pulse of symbol duration $T$, | ||
| + | * rectangular impulse response of the matched filter of the same width $T$. | ||
| − | === | + | |
| + | All phase diagrams presented here – $\rm (A)$ and $\rm (B)$ and $\rm (C)$ – refer to the detection time points only. Thus, the transitions between the individual discrete-time points are not plotted in this phase diagram. | ||
| + | |||
| + | *An AWGN channel with $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ is present. | ||
| + | *Accordingly, for the bit error probability of the first system considered $\rm (A)$ : | ||
| + | :$$p_{\rm B} = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right )\hspace{0.05cm}.$$ | ||
| + | |||
| + | The phase diagrams $\rm (B)$ and $\rm (C)$ belong to two systems where the 4-QAM was not optimally realized. AWGN noise with $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ is also assumed in each of these. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *This exercise belongs to the chapter [[Modulation_Methods/Quadrature_Amplitude_Modulation|"Quadrature Amplitude Modulation"]]. | ||
| + | *Reference is also made to the page [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation#Phase_offset_between_transmitter_and_receiver|"Phase offset between transmitter and receiver"]] in the book "Digital Signal Transmission". | ||
| + | *Causes and Effects of intersymbol interference are explained in the [[Digital_Signal_Transmission/Causes_and_Effects_of_Intersymbol_Interference|section with the same name]] of the book "Digital Signal Transmission". | ||
| + | *The crosses in the graphs mark possible points in the phase diagrams if no AWGN noise were present. | ||
| + | *The point clouds due to the AWGN noise all have the same diameter. The red cloud appears slightly smaller than the others only because "red" is harder to see on a black background. | ||
| + | *As a sufficiently good approximation for the complementary Gaussian error integral, you can use: | ||
| + | :$${\rm erfc}(x) \approx \frac{1}{\sqrt{\pi}\cdot x} \cdot {\rm e}^{-x^2}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Using the given approximation, calculate the bit error probability of system $\rm (A)$. |
| + | |type="{}"} | ||
| + | System $\rm (A):\ \ p_{\rm B} \ = \ $ { 3.5 3% } $\ \cdot 10^{-5}$ | ||
| + | |||
| + | |||
| + | |||
| + | {What are the properties of system $\rm (B)$ ? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | + There is a phase offset between transmitter and receiver. |
| − | + | - The receiver filter results in intersymbol interference. | |
| + | - There is no degradation compared to system $\rm (A)$. | ||
| + | { What are the properties of system $\rm (C)$ ? | ||
| + | |type="[]"} | ||
| + | - There is a phase offset between transmitter and receiver. | ||
| + | + The receiver filter results in intersymbol interference. | ||
| + | - There is no degradation compared to system $\rm (A)$. | ||
| − | { | + | { Which statements about the error probabilities are correct ? |
| − | |type=" | + | |type="[]"} |
| − | $\ | + | - All three systems have the same bit error probability. |
| + | + The error probability of system $\rm (A)$ is the smallest. | ||
| + | + System $\rm (B)$ has a larger bit error probability than system $\rm (C)$. | ||
| Line 23: | Line 63: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' From $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ ⇒ ${E_{\rm B}}/{N_0} = 10^{0.9}\approx 7.95 \hspace{0.05cm}$ follows:$ |
| − | '''2 | + | *With the given approximation, it further holds: |
| − | '''3 | + | :$$p_{\rm B} = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \approx \frac{1}{2 \cdot\sqrt{\pi \cdot{E_{\rm B}}/{N_0}} } \cdot {\rm e}^{-{E_{\rm B}}/{N_0}} = {1}/{2 \cdot\sqrt{7.95 \cdot \pi }} \cdot {\rm e}^{-7.95}\approx \hspace{0.15cm}\underline {3.5 \cdot 10^{-5}\hspace{0.05cm}}.$$ |
| − | '''4 | + | *The exact value $p_{\rm B}\hspace{0.15cm}\underline { = 3.3 · 10^{–5}}$ is only slightly smaller. |
| − | + | ||
| − | + | ||
| − | + | ||
| + | '''(2)''' <u>Answer 1</u> is correct: | ||
| + | *Due to a phase shift of $Δϕ_{\rm T} = 30^\circ$, the phase diagram was rotated, resulting in degradation. | ||
| + | *The two components $\rm I$ and $\rm Q$ influence each other, but there is no intersymbol interference as in system $\rm (C)$. | ||
| + | *A "Nyquist system" never leads to intersymbol interference. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' <u>Answer 2</u> is correct: | ||
| + | *In particular, the nine crosses in each quadrant of the phase diagram $\rm (C)$, which mark the noise-free case, show the influence of intersymbol interference. | ||
| + | *Instead of the optimal receiver filter for a rectangular basic transmission pulse $g_s(t)$ ⇒ rectangular impulse response $h_{\rm E}(t)$ , a [[Signal_Representation/Special_Cases_of_Pulses#Gaussian_pulse|Gaussian low-pass filter]] with (normalized) cutoff frequency $f_{\rm G} · T = 0.6$ was used here. | ||
| + | *This causes intersymbol interference. Even without noise, there are nine crosses in each quadrant indicating one leader and one follower per component. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' <u>Answers 2 and 3</u> are correct: | ||
| + | *Systems $\rm (B)$ and $\rm (C)$ are not optimal. This already shows that statement 1 is not correct. | ||
| + | * In contrast, Answer 2 is right. Every 4-QAM system, which follows the matched filter principle and additionally fulfills the first Nyquist criterion, has the error probability given above: | ||
| + | :$$p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$ | ||
| + | *Thus, the so-called "root-Nyquist configuration", which was treated for example in Exercise 4.12, has exactly the same error probability as system $\rm (A)$ and also the same phase diagram at the detection times. The transitions between the individual points are nevertheless different. | ||
| + | *The third statement is also true. One can already recognize incorrect decisions from the phase diagram of system $\rm (B)$, and this will always be the case when the points do not match the quadrants in terms of color. | ||
| + | |||
| + | |||
| + | The error probabilities of system $\rm (B)$ and system $\rm (C)$ are derived in the book "Digital Signal Transmission". The results of a system simulation confirm the above statements: | ||
| + | * System $\rm (A)$: $p_{\rm B} ≈ 3.3 · 10^{–5}$ (see Question 1), | ||
| + | * System $\rm (B)$: $p_{\rm B} ≈ 3.5 · 10^{–2}$, | ||
| + | * System $\rm (C)$: $p_{\rm B} ≈ 2.4 · 10^{–4}$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^4.3 Quadrature Amplitude Modulation^]] |
Latest revision as of 16:53, 19 April 2022
Graph $\rm (A)$ shows the phase diagram of the 4-QAM after the matched filter, where an optimal realization form was chosen in the case of AWGN noise under the constraint of "peak limiting":
- rectangular basic transmision pulse of symbol duration $T$,
- rectangular impulse response of the matched filter of the same width $T$.
All phase diagrams presented here – $\rm (A)$ and $\rm (B)$ and $\rm (C)$ – refer to the detection time points only. Thus, the transitions between the individual discrete-time points are not plotted in this phase diagram.
- An AWGN channel with $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ is present.
- Accordingly, for the bit error probability of the first system considered $\rm (A)$ :
- $$p_{\rm B} = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right )\hspace{0.05cm}.$$
The phase diagrams $\rm (B)$ and $\rm (C)$ belong to two systems where the 4-QAM was not optimally realized. AWGN noise with $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ is also assumed in each of these.
Hints:
- This exercise belongs to the chapter "Quadrature Amplitude Modulation".
- Reference is also made to the page "Phase offset between transmitter and receiver" in the book "Digital Signal Transmission".
- Causes and Effects of intersymbol interference are explained in the section with the same name of the book "Digital Signal Transmission".
- The crosses in the graphs mark possible points in the phase diagrams if no AWGN noise were present.
- The point clouds due to the AWGN noise all have the same diameter. The red cloud appears slightly smaller than the others only because "red" is harder to see on a black background.
- As a sufficiently good approximation for the complementary Gaussian error integral, you can use:
- $${\rm erfc}(x) \approx \frac{1}{\sqrt{\pi}\cdot x} \cdot {\rm e}^{-x^2}.$$
Questions
Solution
- With the given approximation, it further holds:
- $$p_{\rm B} = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \approx \frac{1}{2 \cdot\sqrt{\pi \cdot{E_{\rm B}}/{N_0}} } \cdot {\rm e}^{-{E_{\rm B}}/{N_0}} = {1}/{2 \cdot\sqrt{7.95 \cdot \pi }} \cdot {\rm e}^{-7.95}\approx \hspace{0.15cm}\underline {3.5 \cdot 10^{-5}\hspace{0.05cm}}.$$
- The exact value $p_{\rm B}\hspace{0.15cm}\underline { = 3.3 · 10^{–5}}$ is only slightly smaller.
(2) Answer 1 is correct:
- Due to a phase shift of $Δϕ_{\rm T} = 30^\circ$, the phase diagram was rotated, resulting in degradation.
- The two components $\rm I$ and $\rm Q$ influence each other, but there is no intersymbol interference as in system $\rm (C)$.
- A "Nyquist system" never leads to intersymbol interference.
(3) Answer 2 is correct:
- In particular, the nine crosses in each quadrant of the phase diagram $\rm (C)$, which mark the noise-free case, show the influence of intersymbol interference.
- Instead of the optimal receiver filter for a rectangular basic transmission pulse $g_s(t)$ ⇒ rectangular impulse response $h_{\rm E}(t)$ , a Gaussian low-pass filter with (normalized) cutoff frequency $f_{\rm G} · T = 0.6$ was used here.
- This causes intersymbol interference. Even without noise, there are nine crosses in each quadrant indicating one leader and one follower per component.
(4) Answers 2 and 3 are correct:
- Systems $\rm (B)$ and $\rm (C)$ are not optimal. This already shows that statement 1 is not correct.
- In contrast, Answer 2 is right. Every 4-QAM system, which follows the matched filter principle and additionally fulfills the first Nyquist criterion, has the error probability given above:
- $$p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$
- Thus, the so-called "root-Nyquist configuration", which was treated for example in Exercise 4.12, has exactly the same error probability as system $\rm (A)$ and also the same phase diagram at the detection times. The transitions between the individual points are nevertheless different.
- The third statement is also true. One can already recognize incorrect decisions from the phase diagram of system $\rm (B)$, and this will always be the case when the points do not match the quadrants in terms of color.
The error probabilities of system $\rm (B)$ and system $\rm (C)$ are derived in the book "Digital Signal Transmission". The results of a system simulation confirm the above statements:
- System $\rm (A)$: $p_{\rm B} ≈ 3.3 · 10^{–5}$ (see Question 1),
- System $\rm (B)$: $p_{\rm B} ≈ 3.5 · 10^{–2}$,
- System $\rm (C)$: $p_{\rm B} ≈ 2.4 · 10^{–4}$.