Difference between revisions of "Aufgaben:Exercise 4.3: PDF Comparison with Regard to Differential Entropy"
m (Text replacement - "„" to """) |
|||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Differential_Entropy |
}} | }} | ||
| − | [[File: | + | [[File:EN_Inf_A_4_3_v2.png|right|frame|$h(X)$ for four probability density functions]] |
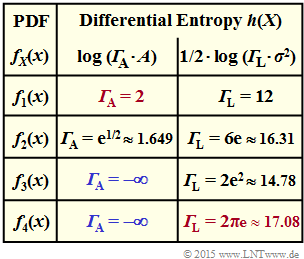
| − | + | The adjacent table shows the comparison result with respect to the differential entropy $h(X)$ for | |
| − | * | + | * the [[Theory_of_Stochastic_Signals/Gleichverteilte_Zufallsgrößen|uniform distribution]] ⇒ $f_X(x) = f_1(x)$: |
| − | :$$f_1(x) = \left\{ \begin{array}{c} 1/(2A) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |x| \le A \\ {\rm | + | :$$f_1(x) = \left\{ \begin{array}{c} 1/(2A) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |x| \le A \\ {\rm else} \\ \end{array} |
,$$ | ,$$ | ||
| − | * | + | * the [[Aufgaben:Exercise_3.1Z:_Triangular_PDF|triangular distribution]] ⇒ $f_X(x) = f_2(x)$: |
| − | :$$f_2(x) = \left\{ \begin{array}{c} 1/A \cdot \big [1 - |x|/A \big ] \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |x| \le A \\ {\rm | + | :$$f_2(x) = \left\{ \begin{array}{c} 1/A \cdot \big [1 - |x|/A \big ] \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |x| \le A \\ {\rm else} \\ \end{array} |
,$$ | ,$$ | ||
| − | * | + | * the [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#Two-sided_exponential_distribution_-_Laplace_distribution|Laplace distribution]] ⇒ $f_X(x) = f_3(x)$: |
:$$f_3(x) = \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm} \cdot \hspace{0.05cm}|x|}\hspace{0.05cm}.$$ | :$$f_3(x) = \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm} \cdot \hspace{0.05cm}|x|}\hspace{0.05cm}.$$ | ||
| − | + | The values for the [[Theory_of_Stochastic_Signals/Gaußverteilte_Zufallsgrößen|Gaussian distribution]] ⇒ $f_X(x) = f_4(x)$ with | |
:$$f_4(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \cdot {\rm e}^{ | :$$f_4(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \cdot {\rm e}^{ | ||
- \hspace{0.05cm}{x ^2}/{(2 \sigma^2})}$$ | - \hspace{0.05cm}{x ^2}/{(2 \sigma^2})}$$ | ||
| − | + | are not yet entered here. These are to be determined in subtasks '''(1)''' to '''(3)''' . | |
| − | + | Each probability density function $\rm (PDF)$ considered here is | |
| − | * | + | * symmetric about $x = 0$ ⇒ $f_X(-x) = f_X(x)$ |
| − | * | + | * and thus zero mean ⇒ $m_1 = 0$. |
| − | In | + | In all cases considered here, the differential entropy can be represented as follows: |
| − | * | + | *Under the constraint $|X| ≤ A$ ⇒ [[Information_Theory/Differentielle_Entropie#Proof:_Maximum_differential_entropy_with_peak_constraint|peak constraint]] $($German: "Spitzenwertbegrenzung" or "Amplitudenbegrenzung" ⇒ Identifier: $\rm A)$: |
:$$h(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm}\rm A} \cdot A) | :$$h(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm}\rm A} \cdot A) | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * | + | *Under the constraint ${\rm E}\big [|X – m_1|^2 \big ] ≤ σ^2$ ⇒ [[Information_Theory/Differentielle_Entropie#Proof:_Maximum_differential_entropy_with_power_constraint|power constraint]] $($German: "Leistungsbegrenzung" ⇒ Identifier: $\rm L)$: |
:$$h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm}\rm L} \cdot \sigma^2) | :$$h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm}\rm L} \cdot \sigma^2) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The larger the respective parameter ${\it \Gamma}_{\hspace{-0.01cm}\rm A}$ or ${\it \Gamma}_{\hspace{-0.01cm}\rm L}$ is, the more favorable is the present PDF in terms of differential entropy for the agreed constraint. | |
| Line 40: | Line 40: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Information_Theory/Differentielle_Entropie|Differential Entropy]]. |
| − | * | + | *Useful hints for solving this task can be found in particular on the pages |
| − | ::[[Information_Theory/Differentielle_Entropie# | + | ::[[Information_Theory/Differentielle_Entropie#Differential_entropy_of_some_peak-constrained_random_variables|Differential entropy of some peak-constrained random variables]], |
| − | ::[[Information_Theory/Differentielle_Entropie# | + | ::[[Information_Theory/Differentielle_Entropie#Differential_entropy_of_some_power-constrained_random_variables|Differential entropy of some power-constrained random variables]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which equation is valid for the logarithm of the Gaussian PDF? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + It holds: $\ln \big[f_X(x) \big] = \ln (A) - x^2/(2 \sigma^2)$ with $A = f_X(x=0)$. |
| − | - Es | + | - Es It holds: $\ln \big [f_X(x) \big] = A - \ln (x^2/(2 \sigma^2)$ with $A = f_X(x=0)$. |
| − | { | + | {Which equation holds for the differential entropy of the Gaussian PDF? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + It holds: $h(X)= 1/2 \cdot \ln (2\pi\hspace{0.05cm}{\rm e}\hspace{0.01cm}\cdot\hspace{0.01cm}\sigma^2)$ with the pseudo-unit "nat". |
| − | + | + | + It holds: $h(X)= 1/2 \cdot \log_2 (2\pi\hspace{0.05cm}{\rm e}\hspace{0.01cm}\cdot\hspace{0.01cm}\sigma^2)$ with the pseudo-unit "bit". |
| − | { | + | {Complete the missing entry for the Gaussian PDF in the above table. |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_{\rm L} \ = \ $ { 17.08 3% } | ${\it \Gamma}_{\rm L} \ = \ $ { 17.08 3% } | ||
| − | { | + | {What values are obtained for the Gaussian PDF with the DC component $m_1 = \sigma = 1$? |
|type="{}"} | |type="{}"} | ||
$P/\sigma^2 \ = \ $ { 2 3% } | $P/\sigma^2 \ = \ $ { 2 3% } | ||
$h(X) \ = \ $ { 2.047 3% } $\ \rm bit$ | $h(X) \ = \ $ { 2.047 3% } $\ \rm bit$ | ||
| − | { | + | {Which of the statements are true for the differential entropy $h(X)$ considering the "power constraint" ${\rm E}\big[|X – m_1|^2\big] ≤ σ^2$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The Gaussian PDF ⇒ $f_4(x)$ leads to the maximum $h(X)$. |
| − | - | + | - The uniform PDF ⇒ $f_1(x)$ leads to the maximum $h(X)$. |
| − | - | + | - The triangular PDF ⇒ $f_2(x)$ is very unfavorable because it is peak-constrained. |
| − | + | + | + The triangular PDF ⇒ $f_2(x)$ is more favorable than the Laplace PDF ⇒ $f_3(x)$. |
| − | { | + | {Which of the statements are true for "peak constraint" to the range $|X| ≤ A$. The maximum differential entropy $h(X)$ is obtained for |
|type="[]"} | |type="[]"} | ||
| − | - | + | - a Gaussian PDF ⇒ $f_4(x)$ followed by a constraint ⇒ $|X| ≤ A$, |
| − | + | + | + the uniform PDF ⇒ $f_1(x)$, |
| − | - | + | - the triangular PDF ⇒ $f_2(x)$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' We assume the zero mean Gaussian PDF: |
:$$f_X(x) = f_4(x) =A \cdot {\rm exp} [ | :$$f_X(x) = f_4(x) =A \cdot {\rm exp} [ | ||
- \hspace{0.05cm}\frac{x ^2}{2 \sigma^2}] | - \hspace{0.05cm}\frac{x ^2}{2 \sigma^2}] | ||
| − | \hspace{0.5cm}{\rm | + | \hspace{0.5cm}{\rm with}\hspace{0.5cm} |
A = \frac{1}{\sqrt{2\pi \sigma^2}}\hspace{0.05cm}.$$ | A = \frac{1}{\sqrt{2\pi \sigma^2}}\hspace{0.05cm}.$$ | ||
| − | * | + | *Logarithmizing this function, the result is <u>proposed solution 1</u>: |
:$${\rm ln}\hspace{0.1cm} \big [f_X(x) \big ] = {\rm ln}\hspace{0.1cm}(A) + | :$${\rm ln}\hspace{0.1cm} \big [f_X(x) \big ] = {\rm ln}\hspace{0.1cm}(A) + | ||
{\rm ln}\hspace{0.1cm}\left [{\rm exp} ( | {\rm ln}\hspace{0.1cm}\left [{\rm exp} ( | ||
| Line 101: | Line 101: | ||
| − | '''(2)''' <u> | + | '''(2)''' <u>Both proposed solutions</u> are correct: |
| − | * | + | *Using the result from '''(1)''' we obtain for the differential entropy in "nat": |
:$$h_{\rm nat}(X)= -\hspace{-0.1cm} \int_{-\infty}^{+\infty} \hspace{-0.15cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x = | :$$h_{\rm nat}(X)= -\hspace{-0.1cm} \int_{-\infty}^{+\infty} \hspace{-0.15cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x = | ||
- {\rm ln}\hspace{0.1cm}(A) \cdot | - {\rm ln}\hspace{0.1cm}(A) \cdot | ||
| Line 108: | Line 108: | ||
+ \frac{1}{2 \sigma^2} \cdot \int_{-\infty}^{+\infty} \hspace{-0.15cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x = - {\rm ln}\hspace{0.1cm}(A) + {1}/{2} | + \frac{1}{2 \sigma^2} \cdot \int_{-\infty}^{+\infty} \hspace{-0.15cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x = - {\rm ln}\hspace{0.1cm}(A) + {1}/{2} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Here it is taken into account that the first integral is equal to $1$ (PDF area). |
| − | * | + | *The second integral also gives the variance $\sigma^2$ (if, as here, the equal part $m_1 = 0$ ). |
| − | * | + | *Substituting the abbreviation variable $A$, we obtain: |
:$$h_{\rm nat}(X) \hspace{-0.15cm} = \hspace{-0.15cm} - {\rm ln}\hspace{0.05cm}\left (\frac{1}{\sqrt{2\pi \sigma^2}} \right ) + {1}/{2} = {1}/{2}\cdot {\rm ln}\hspace{0.05cm}\left ({2\pi \sigma^2} \right ) + {1}/{2} \cdot {\rm ln}\hspace{0.05cm}\left ( {\rm e} \right ) = {1}/{2} \cdot {\rm ln}\hspace{0.05cm}\left ({{2\pi {\rm e} \cdot \sigma^2}} \right ) | :$$h_{\rm nat}(X) \hspace{-0.15cm} = \hspace{-0.15cm} - {\rm ln}\hspace{0.05cm}\left (\frac{1}{\sqrt{2\pi \sigma^2}} \right ) + {1}/{2} = {1}/{2}\cdot {\rm ln}\hspace{0.05cm}\left ({2\pi \sigma^2} \right ) + {1}/{2} \cdot {\rm ln}\hspace{0.05cm}\left ( {\rm e} \right ) = {1}/{2} \cdot {\rm ln}\hspace{0.05cm}\left ({{2\pi {\rm e} \cdot \sigma^2}} \right ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *If the differential entropy $h(X)$ is not to be given in "nat" but in "bit", choose base $2$ for the logarithm: |
:$$h_{\rm bit}(X) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ({{2\pi {\rm e} \cdot \sigma^2}} \right ) | :$$h_{\rm bit}(X) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ({{2\pi {\rm e} \cdot \sigma^2}} \right ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 119: | Line 119: | ||
| − | '''(3)''' | + | '''(3)''' Thus, according to the implicit definition $h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm}\rm L} \cdot \sigma^2)$ , the parameter is: |
:$${\it \Gamma}_{\rm L} = 2\pi {\rm e} \hspace{0.15cm}\underline{\approx 17.08} | :$${\it \Gamma}_{\rm L} = 2\pi {\rm e} \hspace{0.15cm}\underline{\approx 17.08} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 125: | Line 125: | ||
| − | '''(4)''' | + | '''(4)''' We now consider a Gaussian probability density function with mean $m_1$: |
:$$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \cdot {\rm exp}\left [ | :$$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \cdot {\rm exp}\left [ | ||
- \hspace{0.05cm}\frac{(x -m_1)^2}{2 \sigma^2} \right ] | - \hspace{0.05cm}\frac{(x -m_1)^2}{2 \sigma^2} \right ] | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * The second moment $m_2 = {\rm E}\big [X ^2 \big ]$ can also be called the power $P$, while for the variance holds (this is also the second central moment): |
:$$\sigma^2 = {\rm E}\big [|X – m_1|^2 \big ] = \mu_2.$$ | :$$\sigma^2 = {\rm E}\big [|X – m_1|^2 \big ] = \mu_2.$$ | ||
| − | * | + | *According to Steiner's theorem, $P = m_2 = m_1^2 + \sigma^2$. Thus, assuming $m_1 = \sigma = 1$ ⇒ $\underline{P/\sigma^2 = 2}$. |
| − | * | + | *Due to the DC component, the power is indeed doubled. However, this does not change anything in the differential entropy. Thus, it is still valid: |
:$$h(X) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ({{2\pi {\rm e} \cdot \sigma^2}} \right )= {1}/{2} \cdot {\rm log}_2\hspace{0.05cm} (17.08)\hspace{0.15cm}\underline{\approx 2.047\,{\rm bit}} | :$$h(X) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ({{2\pi {\rm e} \cdot \sigma^2}} \right )= {1}/{2} \cdot {\rm log}_2\hspace{0.05cm} (17.08)\hspace{0.15cm}\underline{\approx 2.047\,{\rm bit}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | [[File: | + | [[File:EN_Inf_A_4_3_M_v2L.png|right|frame|Completed results table for $h(X)$]] |
| − | '''(5)''' | + | '''(5)''' Correct are the proposed solutions '''(1)''' and '''(4)'''. The numerical values of the characteristics ${\it \Gamma}_{\rm L}$ and ${\it \Gamma}_{\rm A}$ are also entered in the completed table on the right. |
| − | + | A probability density function $f_X(x)$ is always particularly favorable under power constraints if the value ${\it \Gamma}_{\rm L}$ (right column) is as large as possible. Then the differential entropy $h(X)$ is also large. | |
| − | + | The numerical results can be interpreted as follows: | |
| − | * | + | * As is proved in the theory part, the Gaussian PDF $f_4(x)$ leads here to the largest possible ${\it \Gamma}_{\rm L} ≈ 17.08$ ⇒ the <u>proposed solution 1</u> is correct (the value in the last column is marked in red). |
| − | * | + | * For the uniform PDF $f_1(x)$ the parameter ${\it \Gamma}_{\rm L} = 12$ is the smallest in the whole table ⇒ the proposed solution 2 is wrong. |
| − | * | + | * The triangular PDF $f_2(x)$ with ${\it \Gamma}_{\rm L} = 16.31$ is more favorable than the uniform PDF ⇒ the proposed solution 3 is wrong. |
| − | * | + | *The triangular PDF $f_2(x)$ is also better than the Laplace PDF $f_2(x) \ \ ({\it \Gamma}_{\rm L} = 14.78)$ ⇒ the <u>proposed solution 4</u> is correct. |
| − | '''(6)''' | + | '''(6)''' Correct is the proposed solution '''(2)'''. A PDF $f_X(x)$ is favorable in terms of differential entropy $h(X)$ under the peak constraint ⇒ $|X| ≤ A$, if the weighting factor ${\it \Gamma}_{\rm A}$ (middle column) is as large as possible: |
| − | * | + | * As shown in the theory section, the uniform distribution $f_1(x)$ leads here to the largest possible ${\it \Gamma}_{\rm A}= 2$ ⇒ the <u>proposed solution 2</u> is correct (the value in the middle column is marked in red). |
| − | * | + | * The triangular PDF $f_2(x)$, which is also peak-constrained, is characterized by a somewhat smaller ${\it \Gamma}_{\rm A}= 1.649$ ⇒ dthe proposed solution 3 is incorrect. |
| − | * | + | * The Gaussian PDF $f_4(x)$ is infinitely extended. A peak constraint on $|X| ≤ A$ leads here to Dirac functions in the PDF ⇒ $h(X) \to - \infty$, see sample solution to Exercise 4.2Z, subtask '''(4)'''. |
| − | * | + | * The same would be true for the Laplace PDF $f_3(x)$ . |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 163: | Line 163: | ||
| − | [[Category:Information Theory: Exercises|^4.1 | + | [[Category:Information Theory: Exercises|^4.1 Differential Entropy^]] |
Latest revision as of 14:08, 28 September 2021
The adjacent table shows the comparison result with respect to the differential entropy $h(X)$ for
- the uniform distribution ⇒ $f_X(x) = f_1(x)$:
- $$f_1(x) = \left\{ \begin{array}{c} 1/(2A) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |x| \le A \\ {\rm else} \\ \end{array} ,$$
- the triangular distribution ⇒ $f_X(x) = f_2(x)$:
- $$f_2(x) = \left\{ \begin{array}{c} 1/A \cdot \big [1 - |x|/A \big ] \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |x| \le A \\ {\rm else} \\ \end{array} ,$$
- the Laplace distribution ⇒ $f_X(x) = f_3(x)$:
- $$f_3(x) = \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm} \cdot \hspace{0.05cm}|x|}\hspace{0.05cm}.$$
The values for the Gaussian distribution ⇒ $f_X(x) = f_4(x)$ with
- $$f_4(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{x ^2}/{(2 \sigma^2})}$$
are not yet entered here. These are to be determined in subtasks (1) to (3) .
Each probability density function $\rm (PDF)$ considered here is
- symmetric about $x = 0$ ⇒ $f_X(-x) = f_X(x)$
- and thus zero mean ⇒ $m_1 = 0$.
In all cases considered here, the differential entropy can be represented as follows:
- Under the constraint $|X| ≤ A$ ⇒ peak constraint $($German: "Spitzenwertbegrenzung" or "Amplitudenbegrenzung" ⇒ Identifier: $\rm A)$:
- $$h(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm}\rm A} \cdot A) \hspace{0.05cm},$$
- Under the constraint ${\rm E}\big [|X – m_1|^2 \big ] ≤ σ^2$ ⇒ power constraint $($German: "Leistungsbegrenzung" ⇒ Identifier: $\rm L)$:
- $$h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm}\rm L} \cdot \sigma^2) \hspace{0.05cm}.$$
The larger the respective parameter ${\it \Gamma}_{\hspace{-0.01cm}\rm A}$ or ${\it \Gamma}_{\hspace{-0.01cm}\rm L}$ is, the more favorable is the present PDF in terms of differential entropy for the agreed constraint.
Hints:
- The exercise belongs to the chapter Differential Entropy.
- Useful hints for solving this task can be found in particular on the pages
Questions
Solution
- $$f_X(x) = f_4(x) =A \cdot {\rm exp} [ - \hspace{0.05cm}\frac{x ^2}{2 \sigma^2}] \hspace{0.5cm}{\rm with}\hspace{0.5cm} A = \frac{1}{\sqrt{2\pi \sigma^2}}\hspace{0.05cm}.$$
- Logarithmizing this function, the result is proposed solution 1:
- $${\rm ln}\hspace{0.1cm} \big [f_X(x) \big ] = {\rm ln}\hspace{0.1cm}(A) + {\rm ln}\hspace{0.1cm}\left [{\rm exp} ( - \hspace{0.05cm}\frac{x ^2}{2 \sigma^2}) \right ] = {\rm ln}\hspace{0.1cm}(A) - \frac{x ^2}{2 \sigma^2}\hspace{0.05cm}.$$
(2) Both proposed solutions are correct:
- Using the result from (1) we obtain for the differential entropy in "nat":
- $$h_{\rm nat}(X)= -\hspace{-0.1cm} \int_{-\infty}^{+\infty} \hspace{-0.15cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x = - {\rm ln}\hspace{0.1cm}(A) \cdot \int_{-\infty}^{+\infty} \hspace{-0.15cm} f_X(x) \hspace{0.1cm}{\rm d}x + \frac{1}{2 \sigma^2} \cdot \int_{-\infty}^{+\infty} \hspace{-0.15cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x = - {\rm ln}\hspace{0.1cm}(A) + {1}/{2} \hspace{0.05cm}.$$
- Here it is taken into account that the first integral is equal to $1$ (PDF area).
- The second integral also gives the variance $\sigma^2$ (if, as here, the equal part $m_1 = 0$ ).
- Substituting the abbreviation variable $A$, we obtain:
- $$h_{\rm nat}(X) \hspace{-0.15cm} = \hspace{-0.15cm} - {\rm ln}\hspace{0.05cm}\left (\frac{1}{\sqrt{2\pi \sigma^2}} \right ) + {1}/{2} = {1}/{2}\cdot {\rm ln}\hspace{0.05cm}\left ({2\pi \sigma^2} \right ) + {1}/{2} \cdot {\rm ln}\hspace{0.05cm}\left ( {\rm e} \right ) = {1}/{2} \cdot {\rm ln}\hspace{0.05cm}\left ({{2\pi {\rm e} \cdot \sigma^2}} \right ) \hspace{0.05cm}.$$
- If the differential entropy $h(X)$ is not to be given in "nat" but in "bit", choose base $2$ for the logarithm:
- $$h_{\rm bit}(X) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ({{2\pi {\rm e} \cdot \sigma^2}} \right ) \hspace{0.05cm}.$$
(3) Thus, according to the implicit definition $h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm}\rm L} \cdot \sigma^2)$ , the parameter is:
- $${\it \Gamma}_{\rm L} = 2\pi {\rm e} \hspace{0.15cm}\underline{\approx 17.08} \hspace{0.05cm}.$$
(4) We now consider a Gaussian probability density function with mean $m_1$:
- $$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \cdot {\rm exp}\left [ - \hspace{0.05cm}\frac{(x -m_1)^2}{2 \sigma^2} \right ] \hspace{0.05cm}.$$
- The second moment $m_2 = {\rm E}\big [X ^2 \big ]$ can also be called the power $P$, while for the variance holds (this is also the second central moment):
- $$\sigma^2 = {\rm E}\big [|X – m_1|^2 \big ] = \mu_2.$$
- According to Steiner's theorem, $P = m_2 = m_1^2 + \sigma^2$. Thus, assuming $m_1 = \sigma = 1$ ⇒ $\underline{P/\sigma^2 = 2}$.
- Due to the DC component, the power is indeed doubled. However, this does not change anything in the differential entropy. Thus, it is still valid:
- $$h(X) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ({{2\pi {\rm e} \cdot \sigma^2}} \right )= {1}/{2} \cdot {\rm log}_2\hspace{0.05cm} (17.08)\hspace{0.15cm}\underline{\approx 2.047\,{\rm bit}} \hspace{0.05cm}.$$
(5) Correct are the proposed solutions (1) and (4). The numerical values of the characteristics ${\it \Gamma}_{\rm L}$ and ${\it \Gamma}_{\rm A}$ are also entered in the completed table on the right.
A probability density function $f_X(x)$ is always particularly favorable under power constraints if the value ${\it \Gamma}_{\rm L}$ (right column) is as large as possible. Then the differential entropy $h(X)$ is also large.
The numerical results can be interpreted as follows:
- As is proved in the theory part, the Gaussian PDF $f_4(x)$ leads here to the largest possible ${\it \Gamma}_{\rm L} ≈ 17.08$ ⇒ the proposed solution 1 is correct (the value in the last column is marked in red).
- For the uniform PDF $f_1(x)$ the parameter ${\it \Gamma}_{\rm L} = 12$ is the smallest in the whole table ⇒ the proposed solution 2 is wrong.
- The triangular PDF $f_2(x)$ with ${\it \Gamma}_{\rm L} = 16.31$ is more favorable than the uniform PDF ⇒ the proposed solution 3 is wrong.
- The triangular PDF $f_2(x)$ is also better than the Laplace PDF $f_2(x) \ \ ({\it \Gamma}_{\rm L} = 14.78)$ ⇒ the proposed solution 4 is correct.
(6) Correct is the proposed solution (2). A PDF $f_X(x)$ is favorable in terms of differential entropy $h(X)$ under the peak constraint ⇒ $|X| ≤ A$, if the weighting factor ${\it \Gamma}_{\rm A}$ (middle column) is as large as possible:
- As shown in the theory section, the uniform distribution $f_1(x)$ leads here to the largest possible ${\it \Gamma}_{\rm A}= 2$ ⇒ the proposed solution 2 is correct (the value in the middle column is marked in red).
- The triangular PDF $f_2(x)$, which is also peak-constrained, is characterized by a somewhat smaller ${\it \Gamma}_{\rm A}= 1.649$ ⇒ dthe proposed solution 3 is incorrect.
- The Gaussian PDF $f_4(x)$ is infinitely extended. A peak constraint on $|X| ≤ A$ leads here to Dirac functions in the PDF ⇒ $h(X) \to - \infty$, see sample solution to Exercise 4.2Z, subtask (4).
- The same would be true for the Laplace PDF $f_3(x)$ .