Aufgaben:Exercise 4.3Z: Dirac-shaped "2D-PDF"

• Return to book

Dirac-shaped 2D– PDF

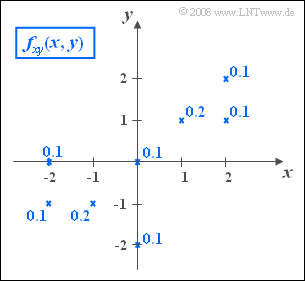
The graph shows the two-dimensional probability density function $f_{xy}(x, y)$  of two discrete random variables  $x$,  $y$.

• This 2D–PDF consists of eight Dirac points,  marked by crosses. 
• The numerical values indicate the corresponding probabilities.
• It can be seen that both  $x$  and  $y$  can take all integer values between the limits  $-2$  and  $+2$.
• The variances of the two random variables are given as follows:   $\sigma_x^2 = 2$,   $\sigma_y^2 = 1.4$.

Hints:

• The exercise belongs to the chapter  Two-Dimensional Random Variables.
• Reference is also made to the chapter  Moments of a Discrete Random Variable

Questions

1

Which of the following statements are true regarding the random variable  $x$?

	The probabilities for  $-2$,  $-1$,    $0$,  $+1$  and  $+2$  are equal.
	The random variable  $x$  is mean-free  $(m_x = 0)$.
	The probability  ${\rm Pr}(x \le 1)=0.9$.

2

Which of the following statements are true with respect to the random variable  $y$?

	The probabilities for  $-2$,  $-1$,    $0$,  $+1$  and  $+2$  are equal.
	The random variable  $y$  is mean-free  $(m_y = 0)$.
	The probability  ${\rm Pr}(y \le 1)=0.9$.

3

Calculate the value of the two-dimensional cumulative distribution function  $\rm (CDF)$  at location  $(+1, +1)$.

$F_{xy}(+1, +1) \ = \ $

4

Calculate the probability that  $x \le 1$  holds,  conditioned on  $y \le 1$  simultaneously.

${\rm Pr}(x ≤ 1\hspace{0.05cm} | \hspace{0.05cm}y ≤ 1)\ = \ $

5

Calculate the joint moment  $m_{xy}$  of the random variables  $x$  and  $y$.

$m_{xy}\ = \ $

6

Calculate the correlation coefficient  $\rho_{xy}$.  Give the equation of the correlation line  $K(x)$  What is its angle to the  $x$–axis?

$\rho_{xy}\ = \ $

$\theta_{y\hspace{0.05cm}→\hspace{0.05cm} x}\ = \ $ $\ \rm degrees$

7

Which of the following statements are true?

	The random variables  $x$  and  $y$  are statistically independent.
	It can already be seen from the given 2D–PDF that  $x$  and  $y$  are statistically dependent on each other.
	From the calculated correlation coefficient  $\rho_{xy}$  one can conclude the statistical dependence between  $x$  and  $y$ .

Solution

Solution

(1)  Correct are the first two answers:

• The marginal probability density function $f_{x}(x)$  is obtained from the 2D PDF $f_{xy}(x, y)$  by integration over  $y$.
• For all possible values  $ x \in \{-2, -1, \ 0, +1, +2\}$  the probabilities are equal  $0.2$.
• It holds  ${\rm Pr}(x \le 1)= 0.8$  and the mean is  $m_x = 0$.

Discrete marginal PDF $f_{y}(y)$

(2)  Correct are the proposed solutions 2 and 3:

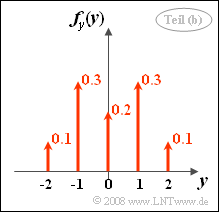
• By integration over  $x$  one obtains the PDF $f_{y}(y)$ sketched on the right.
• Due to symmetry, the mean value  $m_y = 0$ is obtained.
• The probability we are looking for is  ${\rm Pr}(y \le 1)= 0.9$.

(3)  By definition:

$$F_{xy}(r_x, r_y) = {\rm Pr} \big [(x \le r_x)\cap(y\le r_y)\big ].$$

• For  $r_x = r_y = 1$  it follows:

$$F_{xy}(+1, +1) = {\rm Pr}\big [(x \le 1)\cap(y\le 1)\big ].$$

• As can be seen from the 2D PDF on the details page, this probability is  ${\rm Pr}\big [(x \le 1)\cap(y\le 1)\big ]\hspace{0.15cm}\underline{=0.8}$.

(4)  For this, Bayes' theorem can also be used to write:

$$ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = \frac{ \rm Pr\big [(\it x \le \rm 1)\cap(\it y\le \rm 1)\big ]}{ \rm Pr(\it y\le \rm 1)} = \it \frac{F_{xy} \rm (1, \rm 1)}{F_{y}\rm (1)}.$$

• With the results from  (2)  and  (3)  it follows  $ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = 0.8/0.9 = 8/9 \hspace{0.15cm}\underline{=0.889}$.

(5)  According to the definition, the common moment is:

$$m_{xy} = {\rm E}\big[x\cdot y \big] = \sum\limits_{i} {\rm Pr}( x_i \cap y_i)\cdot x_i\cdot y_i. $$

• There remain five Dirac functions with  $x_i \cdot y_i \ne 0$:

$$m_{xy} = \rm 0.1\cdot (-2) (-1) + 0.2\cdot(-1) (-1)+ 0.2\cdot 1\cdot 1 + 0.1\cdot 2\cdot 1+ 0.1\cdot 2\cdot 2\hspace{0.15cm}\underline{=\rm 1.2}.$$

2D PDF and correlation line  $y = K(x)$

(6)  For the correlation coefficient:

$$\rho_{xy} = \frac{\mu_{xy}}{\sigma_x\cdot \sigma_y} = \frac{1.2}{\sqrt{2}\cdot\sqrt{1.4}}\hspace{0.15cm}\underline{=0.717}.$$

• This takes into account that because  $m_x = m_y = 0$  the covariance  $\mu_{xy}$  is equal to the moment  $m_{xy}$  .

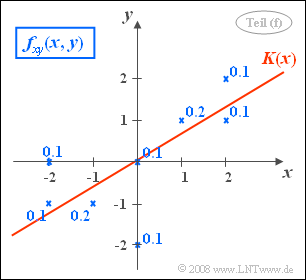
• The equation of the correlation line is:

$$y=\frac{\sigma_y}{\sigma_x}\cdot \rho_{xy}\cdot x = \frac{\mu_{xy}}{\sigma_x^{\rm 2}}\cdot x = \rm 0.6\cdot \it x.$$

• In the picture the straight line  $y = K(x)$  is drawn.  The angle between correlation straight line and  $x$-axis amounts to.

$$\theta_{y\hspace{0.05cm}→\hspace{0.05cm} x} = \arctan(0.6) \hspace{0.15cm}\underline{=31^\circ}.$$

(7)  The correct solutions are solutions 2 and 3:

• If statistically independent, $f_{xy}(x, y) = f_{x}(x) \cdot f_{y}(y)$  should hold, which is not done here.
• From correlatedness  $($follows from  $\rho_{xy} \ne 0)$  it is possible to directly infer statistical dependence,
• because correlation means a special form of statistical dependence,
• namely linear statistical dependence.