Difference between revisions of "Aufgaben:Exercise 5.3Z: Non-Recursive Filter"
| (One intermediate revision by the same user not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
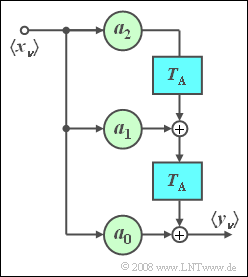
| − | [[File:P_ID608__Sto_Z_5_3.png|right|frame| | + | [[File:P_ID608__Sto_Z_5_3.png|right|frame|Non-recursive filter]] |
Consider the adjacent non-recursive filter with the filter coefficients | Consider the adjacent non-recursive filter with the filter coefficients | ||
:$$a_0 = 1,\quad a_1 = 2,\quad a_2 = 1.$$ | :$$a_0 = 1,\quad a_1 = 2,\quad a_2 = 1.$$ | ||
| Line 9: | Line 9: | ||
We are looking for the respective output sequences $\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle$ when the following value sequences are applied to the input: | We are looking for the respective output sequences $\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle$ when the following value sequences are applied to the input: | ||
| − | *the " | + | *the "DC sequence": |
| − | :$$\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{g_\nu } \right\rangle = \left\langle {\;1,\;1,\;1,\;1,\;1,\;1,\;1,\;1,\;\text{...} } \hspace{0.05cm} \right\rangle | + | :$$\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{g_\nu } \right\rangle = \left\langle {\;1,\;1,\;1,\;1,\;1,\;1,\;1,\;1,\;\text{...} } \hspace{0.05cm} \right\rangle ,$$ |
| − | *the "sinusoidal sequence" with period $T_0 = 4 \cdot T_{\rm A}$: | + | *the "sinusoidal sequence" with period $T_0 = 4 \cdot T_{\rm A}$: |
:$$\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{s_\nu } \right\rangle = \left\langle {\;0,\;1,\;0, - 1,\;0,\;1,\;0, - 1,\;\text{...} } \hspace{0.05cm}\right\rangle .$$ | :$$\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{s_\nu } \right\rangle = \left\langle {\;0,\;1,\;0, - 1,\;0,\;1,\;0, - 1,\;\text{...} } \hspace{0.05cm}\right\rangle .$$ | ||
| Line 19: | Line 19: | ||
| − | + | Notes: | |
| − | |||
| − | |||
| − | |||
*The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Digital_Filters|Digital Filters]] in this book. | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Digital_Filters|Digital Filters]] in this book. | ||
*Reference is also made to some chapters in the book [[Signal Representation]]. | *Reference is also made to some chapters in the book [[Signal Representation]]. | ||
| + | *The HTML5/JavaScript applet [[Applets:Digital_Filters|"Digital Filters"]] illustrates the subject matter of this chapter. | ||
| Line 42: | Line 40: | ||
| − | {What is the output sequence $\left\langle \hspace{0.05cm} {y_\nu } \hspace{0.05cm} \right\rangle$ for the DC sequence $\left\langle \hspace{0.05cm} {g_\nu } \hspace{0.05cm}\right\rangle$ at its input? Interpret this result considering the last subtask. <br>What is the output value for $\nu = 4 $? | + | {What is the output sequence $\left\langle \hspace{0.05cm} {y_\nu } \hspace{0.05cm} \right\rangle$ for the "DC sequence" $\left\langle \hspace{0.05cm} {g_\nu } \hspace{0.05cm}\right\rangle$ at its input? Interpret this result considering the last subtask. <br>What is the output value for $\nu = 4 $? |
|type="{}"} | |type="{}"} | ||
$y_4 \ = \ $ { 4 3% } | $y_4 \ = \ $ { 4 3% } | ||
| − | {What output sequence $\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle$ results for the | + | {What output sequence $\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle$ results for the "sinusoidal sequence" $\left\langle \hspace{0.05cm}{s_\nu } \hspace{0.05cm}\right\rangle$ at its input? <br>What output value results for $\nu = 4 $? |
|type="{}"} | |type="{}"} | ||
$y_4 \ = \ $ { -2.06--1.94 } | $y_4 \ = \ $ { -2.06--1.94 } | ||
| Line 57: | Line 55: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' The impulse response is: $h(t) = \delta (t) + 2 \cdot \delta ( {t - T_{\rm A} } ) + \delta ( {t - 2T_{\rm A} } ).$ | '''(1)''' The impulse response is: $h(t) = \delta (t) + 2 \cdot \delta ( {t - T_{\rm A} } ) + \delta ( {t - 2T_{\rm A} } ).$ | ||
| − | *The maximum is at $T_{\rm A}$ | + | *The maximum is at $T_{\rm A}$ ⇒ $\underline{\nu = 1}$. |
'''(2)''' The frequency response $H(f)$ is the Fourier transform of the impulse response $h(t)$. | '''(2)''' The frequency response $H(f)$ is the Fourier transform of the impulse response $h(t)$. | ||
| − | *The impulse response shifted to the left by $T_{\rm A}$ | + | *The impulse response shifted to the left by $T_{\rm A}$, |
| − | :$$h\hspace{0.05cm}'(t) = \delta ( {t + T_{\rm A} } ) + 2 \cdot \delta ( t ) + \delta ( {t - T_{\rm A} } )$$ | + | ::$$h\hspace{0.05cm}'(t) = \delta ( {t + T_{\rm A} } ) + 2 \cdot \delta ( t ) + \delta ( {t - T_{\rm A} } ),$$ |
:is symmetric at $t= 0$ and accordingly has the purely real frequency response | :is symmetric at $t= 0$ and accordingly has the purely real frequency response | ||
| − | :$$H\hspace{0.05cm}'(f) = 2\big [ {1 + \cos ( {2{\rm{\pi }}fT_{\rm A} } )} \big ].$$ | + | ::$$H\hspace{0.05cm}'(f) = 2\big [ {1 + \cos ( {2{\rm{\pi }}fT_{\rm A} } )} \big ].$$ |
| − | *By applying the shifting theorem, it further follows: | + | *By applying the shifting theorem, it further follows: |
:$$H(f) = 2\big [ {1 + \cos ( {2{\rm{\pi }}fT_{\rm A} } )} \big ] \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}fT_{\rm A} } .$$ | :$$H(f) = 2\big [ {1 + \cos ( {2{\rm{\pi }}fT_{\rm A} } )} \big ] \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}fT_{\rm A} } .$$ | ||
| − | *Consequently, the value of the frequency response at frequency $f=0$ is $H(f = 0)\hspace{0.15cm}\underline{ = 4}$ | + | *Consequently, the value of the frequency response at frequency $f=0$ is |
| + | :$$H(f = 0)\hspace{0.15cm}\underline{ = 4}.$$ | ||
| Line 86: | Line 85: | ||
:$$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{\;0,\;1,\;2,\;0,\; - 2,\;0,\;2,\;0,\; - 2,\;0,\;...\;}\hspace{0.05cm} \right\rangle .$$ | :$$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{\;0,\;1,\;2,\;0,\; - 2,\;0,\;2,\;0,\; - 2,\;0,\;...\;}\hspace{0.05cm} \right\rangle .$$ | ||
| − | *Thus, the value we are looking for is $y_4\hspace{0.15cm}\underline{ = -2}$. | + | *Thus, the value we are looking for is $y_4\hspace{0.15cm}\underline{ = -2}$. |
<b>Another solution:</b> | <b>Another solution:</b> | ||
| − | *The input sequence $\left\langle \hspace{0.05cm}{s_\nu }\hspace{0.05cm} \right\rangle$ is sinusoidal with period $4 \cdot T_{\rm A}$. Accordingly, the | + | *The input sequence $\left\langle \hspace{0.05cm}{s_\nu }\hspace{0.05cm} \right\rangle$ is sinusoidal with period $4 \cdot T_{\rm A}$. Accordingly, the basic frequency is $f_0 = 1/(4 \cdot T_{\rm A})$. |
*At this frequency, the frequency response $H(f)$ has the following value according to subtask '''(2)''': | *At this frequency, the frequency response $H(f)$ has the following value according to subtask '''(2)''': | ||
:$$H( {f = f_0 } ) = 2\big[ {1 + \cos ( {{{\rm{\pi }}}/{2}} )} \big] \cdot {\rm{e}}^{ - {\rm{j\pi /2}}} = 2 \cdot {\rm{e}}^{ - {\rm{j\pi /2}}} .$$ | :$$H( {f = f_0 } ) = 2\big[ {1 + \cos ( {{{\rm{\pi }}}/{2}} )} \big] \cdot {\rm{e}}^{ - {\rm{j\pi /2}}} = 2 \cdot {\rm{e}}^{ - {\rm{j\pi /2}}} .$$ | ||
| − | *Leaving the transient $($completed at $t = T_{\rm A})$ out of consideration, the following relationship between the input and output signals is obtained with $\tau = T_{\rm A}$ $($phase: $90^\circ)$: | + | *Leaving the transient $($completed at $t = T_{\rm A})$ out of consideration, the following relationship between the input and the output signals is obtained with $\tau = T_{\rm A}$ $($phase: $90^\circ)$: |
:$$y(t) = 2 \cdot x( {t - T_{\rm A} } ).$$ | :$$y(t) = 2 \cdot x( {t - T_{\rm A} } ).$$ | ||
| − | *That means: The sine function becomes the | + | *That means: <u>The sine function becomes the function "minus-cosine" with the amplitude 2</u>. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 19:16, 10 February 2022
Consider the adjacent non-recursive filter with the filter coefficients
- $$a_0 = 1,\quad a_1 = 2,\quad a_2 = 1.$$
We are looking for the respective output sequences $\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle$ when the following value sequences are applied to the input:
- the "DC sequence":
- $$\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{g_\nu } \right\rangle = \left\langle {\;1,\;1,\;1,\;1,\;1,\;1,\;1,\;1,\;\text{...} } \hspace{0.05cm} \right\rangle ,$$
- the "sinusoidal sequence" with period $T_0 = 4 \cdot T_{\rm A}$:
- $$\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{s_\nu } \right\rangle = \left\langle {\;0,\;1,\;0, - 1,\;0,\;1,\;0, - 1,\;\text{...} } \hspace{0.05cm}\right\rangle .$$
Notes:
- The exercise belongs to the chapter Digital Filters in this book.
- Reference is also made to some chapters in the book Signal Representation.
- The HTML5/JavaScript applet "Digital Filters" illustrates the subject matter of this chapter.
Questions
Solution
- The maximum is at $T_{\rm A}$ ⇒ $\underline{\nu = 1}$.
(2) The frequency response $H(f)$ is the Fourier transform of the impulse response $h(t)$.
- The impulse response shifted to the left by $T_{\rm A}$,
- $$h\hspace{0.05cm}'(t) = \delta ( {t + T_{\rm A} } ) + 2 \cdot \delta ( t ) + \delta ( {t - T_{\rm A} } ),$$
- is symmetric at $t= 0$ and accordingly has the purely real frequency response
- $$H\hspace{0.05cm}'(f) = 2\big [ {1 + \cos ( {2{\rm{\pi }}fT_{\rm A} } )} \big ].$$
- By applying the shifting theorem, it further follows:
- $$H(f) = 2\big [ {1 + \cos ( {2{\rm{\pi }}fT_{\rm A} } )} \big ] \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}fT_{\rm A} } .$$
- Consequently, the value of the frequency response at frequency $f=0$ is
- $$H(f = 0)\hspace{0.15cm}\underline{ = 4}.$$
(3) The discrete-time convolution of the input sequence $\left\langle \hspace{0.05cm}{g_\nu } \hspace{0.05cm} \right\rangle$ with the impulse response $\left\langle \hspace{0.05cm}{h_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{1, 2, 1 } \hspace{0.05cm}\right\rangle$ results in
- $$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;3,\;4,\;4,\;4,\;4,\;4,\;4,\;4,\;4,\;4,\; \text{...} \;} \right\rangle $$
- In particular, $y_4\hspace{0.15cm}\underline{ = 4}$.
- With the exception of the values $y_0$ and $y_1$ (transient), we also obtain a synchronous sequence at the output with the constant value 4:
- $$y(t) = H( {f = 0} ) \cdot x( t ) = 4 \cdot 1 = 4.$$
(4) Analogous to subtask (3), we now obtain by shifting, weighting with $a_1$, $a_2$, $a_3$ and subsequent superposition:
- $$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{\;0,\;1,\;2,\;0,\; - 2,\;0,\;2,\;0,\; - 2,\;0,\;...\;}\hspace{0.05cm} \right\rangle .$$
- Thus, the value we are looking for is $y_4\hspace{0.15cm}\underline{ = -2}$.
Another solution:
- The input sequence $\left\langle \hspace{0.05cm}{s_\nu }\hspace{0.05cm} \right\rangle$ is sinusoidal with period $4 \cdot T_{\rm A}$. Accordingly, the basic frequency is $f_0 = 1/(4 \cdot T_{\rm A})$.
- At this frequency, the frequency response $H(f)$ has the following value according to subtask (2):
- $$H( {f = f_0 } ) = 2\big[ {1 + \cos ( {{{\rm{\pi }}}/{2}} )} \big] \cdot {\rm{e}}^{ - {\rm{j\pi /2}}} = 2 \cdot {\rm{e}}^{ - {\rm{j\pi /2}}} .$$
- Leaving the transient $($completed at $t = T_{\rm A})$ out of consideration, the following relationship between the input and the output signals is obtained with $\tau = T_{\rm A}$ $($phase: $90^\circ)$:
- $$y(t) = 2 \cdot x( {t - T_{\rm A} } ).$$
- That means: The sine function becomes the function "minus-cosine" with the amplitude 2.