Difference between revisions of "Aufgaben:Exercise 5.4:Is the BSC Model Renewing?"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Binary_Symmetric_Channel_(BSC)}} |
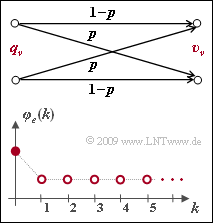
| − | [[File:P_ID1833__Dig_A_5_4.png|right|frame| | + | [[File:P_ID1833__Dig_A_5_4.png|right|frame|Error correlation function (ECF) <br>of the BSC model]] |
| − | + | For the description of digital channel models are mainly used: | |
| − | * | + | * the error distance distribution (EDD) |
:$$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm},$$ | :$$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm},$$ | ||
| − | * | + | * the error correlation function (ECF) |
:$$\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}] | :$$\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}] | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | For a large class of channel models, there is a simple relationship between these descriptive quantities, viz. | |
:$$\varphi_{e}(k) = | :$$\varphi_{e}(k) = | ||
\left\{ \begin{array}{c} \varphi_{e}(0) \\ | \left\{ \begin{array}{c} \varphi_{e}(0) \\ | ||
\sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa)\end{array} \right.\quad | \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa)\end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} f{\rm | + | \begin{array}{*{1}c} f{\rm or }\hspace{0.15cm}k = 0 \hspace{0.05cm}, |
| − | \\ f{\rm | + | \\ f{\rm or }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}$$ |
| − | + | Such channel models are called '''renewing'''. They are characterized by the fact that in them the individual error distances are statistically independent of each other, so that to generate the error sequence the often faster way can be followed via the generation of the error distances, as described in [[Aufgaben:Exercise_5.5:_Error_Sequence_and_Error_Distance_Sequence| "Exercise 5.5"]]. | |
| − | In | + | In this exercise, we want to check whether the BSC model is renewing according to the upper graph. |
| − | * | + | *The error correlation function $\varphi_e(k)$ is shown in the bottom graph. |
| − | * | + | *The probabilities of the individual error distances are given by the BSC model as follows: |
:$${\rm Pr}(a = k) = (1-p)^{k-1}\cdot p \hspace{0.05cm}.$$ | :$${\rm Pr}(a = k) = (1-p)^{k-1}\cdot p \hspace{0.05cm}.$$ | ||
| Line 28: | Line 28: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | * The exercise belongs to the chapter [[Digital_Signal_Transmission/Binary_Symmetric_Channel_(BSC)|"Binary Symmetric Channel (BSC)"]]. |
| − | * | + | * Use the BSC parameter $p = 0.01$ for numerical calculations. |
| − | * | + | * The mean error probability $p_{\rm M}$ then has the same value. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the ECF value $\varphi_e(k = 0)$. |
|type="{}"} | |type="{}"} | ||
$\varphi_e(k = 0) \ = \ ${ 1 3% } $\ \cdot 10^{\rm -2} $ | $\varphi_e(k = 0) \ = \ ${ 1 3% } $\ \cdot 10^{\rm -2} $ | ||
| − | { | + | {Calculate the ECF value $\varphi_e(k = 1)$. |
|type="{}"} | |type="{}"} | ||
$\varphi_e(k = 1) \ = \ ${ 0.01 3% } $\ \cdot 10^{\rm -2} $ | $\varphi_e(k = 1) \ = \ ${ 0.01 3% } $\ \cdot 10^{\rm -2} $ | ||
| − | { | + | {Calculate the ECF value $\varphi_e(k = 2)$. |
|type="{}"} | |type="{}"} | ||
$\varphi_e(k = 2) \ = \ ${ 0.01 3% } $\ \cdot 10^{\rm -2} $ | $\varphi_e(k = 2) \ = \ ${ 0.01 3% } $\ \cdot 10^{\rm -2} $ | ||
| − | { | + | {Provide a reasoned summary of this exercise. |
|type="()"} | |type="()"} | ||
| − | + | + | + The BSC model is renewing. |
| − | - | + | - The BSC model is non-renewing. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Nach der allgemeinen Definition ist $\varphi_e(k = 0) = {\rm E}[e_{\nu}^2]$. | '''(1)''' Nach der allgemeinen Definition ist $\varphi_e(k = 0) = {\rm E}[e_{\nu}^2]$. | ||
Revision as of 16:00, 26 August 2022
For the description of digital channel models are mainly used:
- the error distance distribution (EDD)
- $$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm},$$
- the error correlation function (ECF)
- $$\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}] \hspace{0.05cm}.$$
For a large class of channel models, there is a simple relationship between these descriptive quantities, viz.
- $$\varphi_{e}(k) = \left\{ \begin{array}{c} \varphi_{e}(0) \\ \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa)\end{array} \right.\quad \begin{array}{*{1}c} f{\rm or }\hspace{0.15cm}k = 0 \hspace{0.05cm}, \\ f{\rm or }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}$$
Such channel models are called renewing. They are characterized by the fact that in them the individual error distances are statistically independent of each other, so that to generate the error sequence the often faster way can be followed via the generation of the error distances, as described in "Exercise 5.5".
In this exercise, we want to check whether the BSC model is renewing according to the upper graph.
- The error correlation function $\varphi_e(k)$ is shown in the bottom graph.
- The probabilities of the individual error distances are given by the BSC model as follows:
- $${\rm Pr}(a = k) = (1-p)^{k-1}\cdot p \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Binary Symmetric Channel (BSC)".
- Use the BSC parameter $p = 0.01$ for numerical calculations.
- The mean error probability $p_{\rm M}$ then has the same value.
Questions
Solution
- Wegen $e_{\nu} ∈ \{0, 1\}$ gilt aber gleichzeitig $\varphi_e(k = 0) = {\rm E}[e_\nu]$, was der mittleren Fehlerwahrscheinlichkeit $p_{\rm M} = p$ entspricht ⇒ $\varphi_e(k = 0) \ \underline { = 0.01}$.
(2) Nach der allgemeinen FKF–Definition gilt unter Berücksichtigung des BSC–Modells:
- $$\varphi_{e}(k = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm E}[e_{\nu} \cdot e_{\nu + 1}]={\rm Pr}[e_{\nu} = 1 \cap e_{\nu + 1} = 1] = p \cdot p = p^2 \hspace{0.15cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$
Zum gleichen Ergebnis kommt man über die nur für erneuernde Kanalmodelle gültige Gleichung:
- $$\varphi_{e}(k = 1) = {\rm Pr}(a=1) \cdot \varphi_{e}(0) = p \cdot p = p^2 = 10^{-4}\hspace{0.05cm}.$$
Das bedeutet: Der FKF–Wert $\varphi_e(1)$ spricht nicht dagegen, dass das BSC–Modell erneuernd ist.
(3) Aus der Grafik erkennt man bereits, dass $\varphi_e(k = 2) = \varphi_e(k = 1) = 10^{–4}$ gelten wird. Die explizite Berechnung bestätigt dieses Ergebnis:
- $$\varphi_{e}(k \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2) = {\rm Pr}[e_{\nu} = 1 \cap e_{\nu + 2} = 1] = {\rm Pr}[e_{\nu} = 1 \cap e_{\nu + 1} = 1 \cap e_{\nu + 2} = 1] + {\rm Pr}[e_{\nu} = 1 \cap e_{\nu + 1} = 0 \cap e_{\nu + 2} = 1] \hspace{0.05cm}.$$
- Der erste Term lautet beim BSC-Modell mit den bedingten Wahrscheinlichkeiten (nur erste Ordnung erforderlich):
- $${\rm Pr}[1\hspace{0.1cm}1 \hspace{0.1cm} 1] \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}[e_{\nu +2} = 1 \hspace{0.1cm}|\hspace{0.1cm} e_{\nu + 1} = 1] \cdot {\rm Pr}[e_{\nu +1} = 1 \hspace{0.1cm}|\hspace{0.1cm} e_{\nu } = 1] \cdot {\rm Pr}[ e_{\nu } = 1]=p \cdot p \cdot p = p^3\hspace{0.05cm}.$$
- Entsprechend gilt für den zweiten Term:
- $${\rm Pr}[1\hspace{0.1cm}0 \hspace{0.1cm} 1] \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}[e_{\nu +2} = 1 \hspace{0.1cm}|\hspace{0.1cm} e_{\nu + 1} = 0] \cdot {\rm Pr}[e_{\nu +1} = 0 \hspace{0.1cm}|\hspace{0.1cm} e_{\nu } = 1] \cdot {\rm Pr}[ e_{\nu } = 1]=p \cdot (1-p) \cdot p = p^2 -p^3\hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm} \varphi_{e}(k = 2) = {\rm Pr}[1\hspace{0.1cm}1 \hspace{0.1cm} 1] + {\rm Pr}[1\hspace{0.1cm}0 \hspace{0.1cm} 1] = (p^3) + (p^2 -p^3)= p^2\hspace{0.15cm}\underline { = 10^{-4}}\hspace{0.05cm}.$$
- Mit der nur für erneuernde Kanalmodelle gültigen Gleichung erhält man:
- $$\varphi_{e}(k = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(a=1) \cdot \varphi_{e}(k= 1) + {\rm Pr}(a=2) \cdot \varphi_{e}(k= 0)= p \cdot p^2 + (1-p) \cdot p \cdot p = p^2 \hspace{0.05cm}.$$
- Auch dieses Ergebnis spricht also nicht dagegen, dass das BSC–Modell erneuernd ist.
(4) Die bisherigen Ergebnisse lassen schon darauf schließen, dass das BSC–Modell erneuernd ist. Und auch die Tatsache, dass hier die einzelnen Fehlerabstände statistisch unabhängig voneinander sind, spricht für diese These.
- Als letzten Beweis zeigen wird, dass die Gleichung
- $$\varphi_{e}(k) = \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa)= \varphi_{e}(0) \cdot {\rm Pr}(a = k)+ \sum_{\kappa = 1}^{k-1} \varphi_{e}(k - \kappa) \cdot {\rm Pr}(a = \kappa)$$
- das richtige Ergebnis liefert, wenn $\varphi_e(0) = p$ und $\varphi_e(1) = \ \text{...} \ = \varphi_e(k–1) = p^2$ eingesetzt wird.
- Man erhält
- $$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p \cdot (1-p)^{k-1} \cdot p + p^2 \cdot \sum_{\kappa = 1}^{k-1} (1-p)^{\kappa-1} \cdot p =p^2 \cdot (1-p)^{k-1} + p^3 \cdot \sum_{\kappa = 0}^{k-2} (1-p)^{\kappa}\hspace{0.05cm}.$$
- Mit der Summenformel einer geometrischen Reihe
- $$\sum_{\kappa = 0}^{n} x^{\kappa} = \frac{1 - x^{n+1}}{1 - x}\hspace{0.05cm},$$
- lässt sich dieser Ausdruck wie folgt darstellen:
- $$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p^2 \cdot (1-p)^{k-1} + p^3 \cdot \frac{1 - (1-p)^{k-1}}{1 - (1-p)}= p^2 \cdot \left [ (1-p)^{k-1} + 1 - (1-p)^{k-1} \right ] = p^2\hspace{0.05cm}.$$
- Das bedeutet: Das BSC–Modell ist tatsächlich erneuernd ⇒ Lösungsvorschlag 1.