Difference between revisions of "Aufgaben:Exercise 5.4:Is the BSC Model Renewing?"
From LNTwww
m (Text replacement - "Category:Aufgaben zu Digitalsignalübertragung" to "Category:Digital Signal Transmission: Exercises") |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Binary_Symmetric_Channel_(BSC)}} |
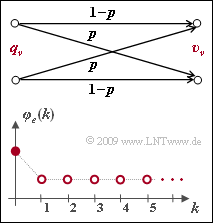
| − | [[File:P_ID1833__Dig_A_5_4.png|right|frame| | + | [[File:P_ID1833__Dig_A_5_4.png|right|frame|Error correlation function $\rm (ECF)$ of the BSC model]] |
| − | + | For the description of digital channel models are mainly used: | |
| − | * | + | * the error distance distribution $\rm (EDD)$ |
:$$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm},$$ | :$$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm},$$ | ||
| − | * | + | * the error correlation function $\rm (ECF)$ |
:$$\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}] | :$$\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}] | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | For a large class of channel models, there is a simple relationship between these descriptive quantities, viz. | |
:$$\varphi_{e}(k) = | :$$\varphi_{e}(k) = | ||
\left\{ \begin{array}{c} \varphi_{e}(0) \\ | \left\{ \begin{array}{c} \varphi_{e}(0) \\ | ||
\sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa)\end{array} \right.\quad | \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa)\end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} f{\rm | + | \begin{array}{*{1}c} f{\rm or }\hspace{0.15cm}k = 0 \hspace{0.05cm}, |
| − | \\ f{\rm | + | \\ f{\rm or }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}$$ |
| − | + | Such channel models are called "'''renewing'''". | |
| − | In | + | *They are characterized by the fact that in them the individual error distances are statistically independent of each other, |
| − | * | + | *so that to generate the error sequence the often faster way can be followed via the generation of the error distances, as described in [[Aufgaben:Exercise_5.5:_Error_Sequence_and_Error_Distance_Sequence| "Exercise 5.5"]]. |
| − | * | + | |
| + | |||
| + | In this exercise, we want to check whether the BSC model is renewing according to the upper graph. | ||
| + | *The error correlation function $\varphi_e(k)$ is shown in the bottom graph. | ||
| + | |||
| + | *The probabilities of the individual error distances are given by the BSC model as follows: | ||
:$${\rm Pr}(a = k) = (1-p)^{k-1}\cdot p \hspace{0.05cm}.$$ | :$${\rm Pr}(a = k) = (1-p)^{k-1}\cdot p \hspace{0.05cm}.$$ | ||
| Line 28: | Line 33: | ||
| − | + | <u>Notes:</u> | |
| − | * | + | * The exercise belongs to the chapter [[Digital_Signal_Transmission/Binary_Symmetric_Channel_(BSC)|"Binary Symmetric Channel"]]. |
| − | * | + | |
| − | + | * Use the BSC parameter $p = 0.01$ for numerical calculations. The mean error probability $p_{\rm M}$ then has the same value. | |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the ECF value $\varphi_e(k = 0)$. |
|type="{}"} | |type="{}"} | ||
$\varphi_e(k = 0) \ = \ ${ 1 3% } $\ \cdot 10^{\rm -2} $ | $\varphi_e(k = 0) \ = \ ${ 1 3% } $\ \cdot 10^{\rm -2} $ | ||
| − | { | + | {Calculate the ECF value $\varphi_e(k = 1)$. |
|type="{}"} | |type="{}"} | ||
$\varphi_e(k = 1) \ = \ ${ 0.01 3% } $\ \cdot 10^{\rm -2} $ | $\varphi_e(k = 1) \ = \ ${ 0.01 3% } $\ \cdot 10^{\rm -2} $ | ||
| − | { | + | {Calculate the ECF value $\varphi_e(k = 2)$. |
|type="{}"} | |type="{}"} | ||
$\varphi_e(k = 2) \ = \ ${ 0.01 3% } $\ \cdot 10^{\rm -2} $ | $\varphi_e(k = 2) \ = \ ${ 0.01 3% } $\ \cdot 10^{\rm -2} $ | ||
| − | { | + | {Provide a reasoned summary of this exercise. |
|type="()"} | |type="()"} | ||
| − | + | + | + The BSC model is renewing. |
| − | - | + | - The BSC model is non-renewing. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' According to the general definition, $\varphi_e(k = 0) = {\rm E}[e_{\nu}^2]$. |
| − | * | + | *However, because of $e_{\nu} ∈ \{0, 1\}$ ⇒ $\varphi_e(k = 0) = {\rm E}[e_\nu]$, holds simultaneously, which corresponds to the mean error probability $p_{\rm M} = p$ ⇒ $\varphi_e(k = 0) \ \underline { = 0.01}$. |
| − | '''(2)''' | + | '''(2)''' According to the general ECF definition, considering the BSC model: |
:$$\varphi_{e}(k = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm E}[e_{\nu} \cdot e_{\nu + 1}]={\rm Pr}[e_{\nu} = 1 \cap | :$$\varphi_{e}(k = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm E}[e_{\nu} \cdot e_{\nu + 1}]={\rm Pr}[e_{\nu} = 1 \cap | ||
e_{\nu + 1} = 1] = p \cdot p = p^2 \hspace{0.15cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$ | e_{\nu + 1} = 1] = p \cdot p = p^2 \hspace{0.15cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$ | ||
| − | + | *The same result is obtained via the equation valid only for renewing channel models: | |
:$$\varphi_{e}(k = 1) = {\rm Pr}(a=1) \cdot \varphi_{e}(0) = p \cdot | :$$\varphi_{e}(k = 1) = {\rm Pr}(a=1) \cdot \varphi_{e}(0) = p \cdot | ||
p = p^2 = 10^{-4}\hspace{0.05cm}.$$ | p = p^2 = 10^{-4}\hspace{0.05cm}.$$ | ||
| − | + | *That means: The ECF value $\varphi_e(1)$ does not argue against the BSC model being renewing. | |
| − | '''(3)''' | + | '''(3)''' From the graph, we can already see that $\varphi_e(k = 2) = \varphi_e(k = 1) = 10^{–4}$ will hold. The explicit calculation confirms this result: |
:$$\varphi_{e}(k \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2) = {\rm | :$$\varphi_{e}(k \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2) = {\rm | ||
Pr}[e_{\nu} = 1 \cap e_{\nu + 2} = 1] = | Pr}[e_{\nu} = 1 \cap e_{\nu + 2} = 1] = | ||
| Line 82: | Line 87: | ||
e_{\nu + 1} = 0 \cap e_{\nu + 2} = 1] \hspace{0.05cm}.$$ | e_{\nu + 1} = 0 \cap e_{\nu + 2} = 1] \hspace{0.05cm}.$$ | ||
| − | * | + | *The first term in the BSC model with the conditional probabilities $($only first order required$)$ is: |
:$${\rm Pr}[1\hspace{0.1cm}1 \hspace{0.1cm} 1] \hspace{-0.1cm} \ = \ | :$${\rm Pr}[1\hspace{0.1cm}1 \hspace{0.1cm} 1] \hspace{-0.1cm} \ = \ | ||
\hspace{-0.1cm}{\rm Pr}[e_{\nu +2} = 1 | \hspace{-0.1cm}{\rm Pr}[e_{\nu +2} = 1 | ||
| Line 90: | Line 95: | ||
p^3\hspace{0.05cm}.$$ | p^3\hspace{0.05cm}.$$ | ||
| − | * | + | *Correspondingly, for the second term: |
:$${\rm Pr}[1\hspace{0.1cm}0 \hspace{0.1cm} 1] \hspace{-0.1cm} \ = \ | :$${\rm Pr}[1\hspace{0.1cm}0 \hspace{0.1cm} 1] \hspace{-0.1cm} \ = \ | ||
\hspace{-0.1cm}{\rm Pr}[e_{\nu +2} = 1 | \hspace{-0.1cm}{\rm Pr}[e_{\nu +2} = 1 | ||
| Line 102: | Line 107: | ||
10^{-4}}\hspace{0.05cm}.$$ | 10^{-4}}\hspace{0.05cm}.$$ | ||
| − | * | + | *Using the equation valid only for renewing channel models, we obtain: |
:$$\varphi_{e}(k = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm | :$$\varphi_{e}(k = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm | ||
Pr}(a=1) \cdot \varphi_{e}(k= 1) + {\rm Pr}(a=2) \cdot | Pr}(a=1) \cdot \varphi_{e}(k= 1) + {\rm Pr}(a=2) \cdot | ||
| Line 108: | Line 113: | ||
\cdot p = p^2 \hspace{0.05cm}.$$ | \cdot p = p^2 \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, this result also does not argue against the BSC model being renewing. |
| − | '''(4)''' | + | '''(4)''' The previous results already suggest that the BSC model is renewing. |
| − | * | + | *And also the fact that here the individual error distances are statistically independent of each other speaks in favor of this thesis. |
| + | |||
| + | *As a final proof, we show that the equation | ||
:$$\varphi_{e}(k) = \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot | :$$\varphi_{e}(k) = \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot | ||
\varphi_{e}(k - \kappa)= \varphi_{e}(0) \cdot {\rm Pr}(a = k)+ | \varphi_{e}(k - \kappa)= \varphi_{e}(0) \cdot {\rm Pr}(a = k)+ | ||
| Line 121: | Line 128: | ||
\kappa)$$ | \kappa)$$ | ||
| − | : | + | :yields the correct result when $\varphi_e(0) = p$ and $\varphi_e(1) = \ \text{...} \ = \varphi_e(k–1) = p^2$ are used. |
| − | * | + | |
| + | *One obtains | ||
:$$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p \cdot | :$$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p \cdot | ||
(1-p)^{k-1} \cdot p + p^2 \cdot \sum_{\kappa = 1}^{k-1} | (1-p)^{k-1} \cdot p + p^2 \cdot \sum_{\kappa = 1}^{k-1} | ||
| Line 128: | Line 136: | ||
\cdot \sum_{\kappa = 0}^{k-2} (1-p)^{\kappa}\hspace{0.05cm}.$$ | \cdot \sum_{\kappa = 0}^{k-2} (1-p)^{\kappa}\hspace{0.05cm}.$$ | ||
| − | * | + | *Using the summation formula of a geometric series |
:$$\sum_{\kappa = 0}^{n} x^{\kappa} = \frac{1 - x^{n+1}}{1 - | :$$\sum_{\kappa = 0}^{n} x^{\kappa} = \frac{1 - x^{n+1}}{1 - | ||
x}\hspace{0.05cm},$$ | x}\hspace{0.05cm},$$ | ||
| − | : | + | :this expression can be represented as follows: |
:$$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p^2 \cdot | :$$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p^2 \cdot | ||
(1-p)^{k-1} + p^3 \cdot \frac{1 - (1-p)^{k-1}}{1 - | (1-p)^{k-1} + p^3 \cdot \frac{1 - (1-p)^{k-1}}{1 - | ||
| Line 138: | Line 146: | ||
(1-p)^{k-1} + 1 - (1-p)^{k-1} \right ] = p^2\hspace{0.05cm}.$$ | (1-p)^{k-1} + 1 - (1-p)^{k-1} \right ] = p^2\hspace{0.05cm}.$$ | ||
| − | * | + | *This means: The BSC model is in fact renewing ⇒ <u>solution 1</u>. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Digital Signal Transmission: Exercises|^5.2 Binary Symmetric Channel | + | [[Category:Digital Signal Transmission: Exercises|^5.2 Binary Symmetric Channel^]] |
Latest revision as of 16:29, 5 September 2022
For the description of digital channel models are mainly used:
- the error distance distribution $\rm (EDD)$
- $$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm},$$
- the error correlation function $\rm (ECF)$
- $$\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}] \hspace{0.05cm}.$$
For a large class of channel models, there is a simple relationship between these descriptive quantities, viz.
- $$\varphi_{e}(k) = \left\{ \begin{array}{c} \varphi_{e}(0) \\ \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa)\end{array} \right.\quad \begin{array}{*{1}c} f{\rm or }\hspace{0.15cm}k = 0 \hspace{0.05cm}, \\ f{\rm or }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}$$
Such channel models are called "renewing".
- They are characterized by the fact that in them the individual error distances are statistically independent of each other,
- so that to generate the error sequence the often faster way can be followed via the generation of the error distances, as described in "Exercise 5.5".
In this exercise, we want to check whether the BSC model is renewing according to the upper graph.
- The error correlation function $\varphi_e(k)$ is shown in the bottom graph.
- The probabilities of the individual error distances are given by the BSC model as follows:
- $${\rm Pr}(a = k) = (1-p)^{k-1}\cdot p \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Binary Symmetric Channel".
- Use the BSC parameter $p = 0.01$ for numerical calculations. The mean error probability $p_{\rm M}$ then has the same value.
Questions
Solution
(1) According to the general definition, $\varphi_e(k = 0) = {\rm E}[e_{\nu}^2]$.
- However, because of $e_{\nu} ∈ \{0, 1\}$ ⇒ $\varphi_e(k = 0) = {\rm E}[e_\nu]$, holds simultaneously, which corresponds to the mean error probability $p_{\rm M} = p$ ⇒ $\varphi_e(k = 0) \ \underline { = 0.01}$.
(2) According to the general ECF definition, considering the BSC model:
- $$\varphi_{e}(k = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm E}[e_{\nu} \cdot e_{\nu + 1}]={\rm Pr}[e_{\nu} = 1 \cap e_{\nu + 1} = 1] = p \cdot p = p^2 \hspace{0.15cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$
- The same result is obtained via the equation valid only for renewing channel models:
- $$\varphi_{e}(k = 1) = {\rm Pr}(a=1) \cdot \varphi_{e}(0) = p \cdot p = p^2 = 10^{-4}\hspace{0.05cm}.$$
- That means: The ECF value $\varphi_e(1)$ does not argue against the BSC model being renewing.
(3) From the graph, we can already see that $\varphi_e(k = 2) = \varphi_e(k = 1) = 10^{–4}$ will hold. The explicit calculation confirms this result:
- $$\varphi_{e}(k \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2) = {\rm Pr}[e_{\nu} = 1 \cap e_{\nu + 2} = 1] = {\rm Pr}[e_{\nu} = 1 \cap e_{\nu + 1} = 1 \cap e_{\nu + 2} = 1] + {\rm Pr}[e_{\nu} = 1 \cap e_{\nu + 1} = 0 \cap e_{\nu + 2} = 1] \hspace{0.05cm}.$$
- The first term in the BSC model with the conditional probabilities $($only first order required$)$ is:
- $${\rm Pr}[1\hspace{0.1cm}1 \hspace{0.1cm} 1] \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}[e_{\nu +2} = 1 \hspace{0.1cm}|\hspace{0.1cm} e_{\nu + 1} = 1] \cdot {\rm Pr}[e_{\nu +1} = 1 \hspace{0.1cm}|\hspace{0.1cm} e_{\nu } = 1] \cdot {\rm Pr}[ e_{\nu } = 1]=p \cdot p \cdot p = p^3\hspace{0.05cm}.$$
- Correspondingly, for the second term:
- $${\rm Pr}[1\hspace{0.1cm}0 \hspace{0.1cm} 1] \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}[e_{\nu +2} = 1 \hspace{0.1cm}|\hspace{0.1cm} e_{\nu + 1} = 0] \cdot {\rm Pr}[e_{\nu +1} = 0 \hspace{0.1cm}|\hspace{0.1cm} e_{\nu } = 1] \cdot {\rm Pr}[ e_{\nu } = 1]=p \cdot (1-p) \cdot p = p^2 -p^3\hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm} \varphi_{e}(k = 2) = {\rm Pr}[1\hspace{0.1cm}1 \hspace{0.1cm} 1] + {\rm Pr}[1\hspace{0.1cm}0 \hspace{0.1cm} 1] = (p^3) + (p^2 -p^3)= p^2\hspace{0.15cm}\underline { = 10^{-4}}\hspace{0.05cm}.$$
- Using the equation valid only for renewing channel models, we obtain:
- $$\varphi_{e}(k = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(a=1) \cdot \varphi_{e}(k= 1) + {\rm Pr}(a=2) \cdot \varphi_{e}(k= 0)= p \cdot p^2 + (1-p) \cdot p \cdot p = p^2 \hspace{0.05cm}.$$
- Thus, this result also does not argue against the BSC model being renewing.
(4) The previous results already suggest that the BSC model is renewing.
- And also the fact that here the individual error distances are statistically independent of each other speaks in favor of this thesis.
- As a final proof, we show that the equation
- $$\varphi_{e}(k) = \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa)= \varphi_{e}(0) \cdot {\rm Pr}(a = k)+ \sum_{\kappa = 1}^{k-1} \varphi_{e}(k - \kappa) \cdot {\rm Pr}(a = \kappa)$$
- yields the correct result when $\varphi_e(0) = p$ and $\varphi_e(1) = \ \text{...} \ = \varphi_e(k–1) = p^2$ are used.
- One obtains
- $$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p \cdot (1-p)^{k-1} \cdot p + p^2 \cdot \sum_{\kappa = 1}^{k-1} (1-p)^{\kappa-1} \cdot p =p^2 \cdot (1-p)^{k-1} + p^3 \cdot \sum_{\kappa = 0}^{k-2} (1-p)^{\kappa}\hspace{0.05cm}.$$
- Using the summation formula of a geometric series
- $$\sum_{\kappa = 0}^{n} x^{\kappa} = \frac{1 - x^{n+1}}{1 - x}\hspace{0.05cm},$$
- this expression can be represented as follows:
- $$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p^2 \cdot (1-p)^{k-1} + p^3 \cdot \frac{1 - (1-p)^{k-1}}{1 - (1-p)}= p^2 \cdot \left [ (1-p)^{k-1} + 1 - (1-p)^{k-1} \right ] = p^2\hspace{0.05cm}.$$
- This means: The BSC model is in fact renewing ⇒ solution 1.