Difference between revisions of "Aufgaben:Exercise 5.7Z: McCullough Model once more"
| Line 62: | Line 62: | ||
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the probabilities $\alpha_{\rm G}$ and $\alpha_{\rm B}$ that the MC model is in the state "Good" and the state "Bad". |
|type="{}"} | |type="{}"} | ||
$\alpha_{\rm G} \hspace{0.05cm} = \ ${ 0.5975 3% } | $\alpha_{\rm G} \hspace{0.05cm} = \ ${ 0.5975 3% } | ||
$\alpha_{\rm B} \ = \ ${ 0.4025 3% } | $\alpha_{\rm B} \ = \ ${ 0.4025 3% } | ||
| − | { | + | {Determine the mean error distance of the MC model. |
|type="{}"} | |type="{}"} | ||
${\rm E}\big[a\big] \ = \ ${ 100.1 3% } | ${\rm E}\big[a\big] \ = \ ${ 100.1 3% } | ||
| − | { | + | {What is the error correlation function value for $k = 0$? |
|type="{}"} | |type="{}"} | ||
$\varphi_e(k = 0) \ = \ ${ 0.01 3% } | $\varphi_e(k = 0) \ = \ ${ 0.01 3% } | ||
| − | { | + | {Give the error correlation duration $D_{\rm K}$ as a function of the MC parameters $q_{\rm G}, q_{\rm B}, q(\rm G\hspace{0.05cm}|\hspace{0.05cm}B)$ and $q(\rm B\hspace{0.05cm}|\hspace{0.05cm}G)$. <br>Which result is correct? |
|type="()"} | |type="()"} | ||
- $D_{\rm K} = \big [q({\rm B\hspace{0.05cm}|\hspace{0.05cm}G}) + q({\rm G\hspace{0.05cm}|\hspace{0.05cm}B})\big]^{-1} \ -1$, | - $D_{\rm K} = \big [q({\rm B\hspace{0.05cm}|\hspace{0.05cm}G}) + q({\rm G\hspace{0.05cm}|\hspace{0.05cm}B})\big]^{-1} \ -1$, | ||
| Line 81: | Line 81: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For the state probabilities of the GE model was determined in Exercise 5.6Z: |
:$$w_{\rm G} = \frac{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{p(\rm | :$$w_{\rm G} = \frac{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{p(\rm | ||
G\hspace{0.05cm}|\hspace{0.05cm} B) + p(\rm | G\hspace{0.05cm}|\hspace{0.05cm} B) + p(\rm | ||
| Line 90: | Line 90: | ||
}= 0.091\hspace{0.05cm}.$$ | }= 0.091\hspace{0.05cm}.$$ | ||
| − | * | + | *In contrast, for the MC model we obtain: |
:$$\alpha_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{q(\rm | :$$\alpha_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{q(\rm | ||
G\hspace{0.05cm}|\hspace{0.05cm} B)}{q(\rm | G\hspace{0.05cm}|\hspace{0.05cm} B)}{q(\rm | ||
| Line 99: | Line 99: | ||
\alpha_{\rm G} \hspace{0.15cm}\underline {= 0.4025}\hspace{0.05cm}.$$ | \alpha_{\rm G} \hspace{0.15cm}\underline {= 0.4025}\hspace{0.05cm}.$$ | ||
| − | *In | + | *In subtask '''(3)''' of Exercise 5.7, these values have already been determined once, but from the parameters of the equivalent Gilbert-Elliott model. |
| − | '''(2)''' | + | '''(2)''' The mean error distance in the channel state "GOOD" is equal to the reciprocal of the associated error probability $q_{\rm G}$. |
| − | * | + | *Accordingly, the mean error distance in the state "BAD" is $1/q_{\rm B}$. |
| − | * | + | *By weighting with the two state probabilities $\alpha_{\rm G}$ and $\alpha_{\rm B}$, the mean error distance of the MC model as a whole is given by |
:$${\rm E}[a] =\frac{\alpha_{\rm G}}{q_{\rm G}} + \frac{\alpha_{\rm | :$${\rm E}[a] =\frac{\alpha_{\rm G}}{q_{\rm G}} + \frac{\alpha_{\rm | ||
B}}{q_{\rm B}}=\frac{0.5975}{0.0061} + \frac{0.4025}{0.1949} = | B}}{q_{\rm B}}=\frac{0.5975}{0.0061} + \frac{0.4025}{0.1949} = | ||
97.95 + 2.06\hspace{0.15cm}\underline { = 100.1}\hspace{0.05cm}.$$ | 97.95 + 2.06\hspace{0.15cm}\underline { = 100.1}\hspace{0.05cm}.$$ | ||
| − | * | + | *Of course, this value should be exactly the same as for the corresponding GE model. |
| − | * | + | *The small deviation of $0.1$ is due to rounding errors. |
| − | '''(3)''' | + | '''(3)''' Again, the relation $\varphi_e(k = 0) = p_{\rm M}$ holds. |
| − | * | + | *However, the mean error probability is equal to the reciprocal of the mean error distance ${\rm E}[a]$. |
| − | * | + | *It follows that $\varphi_e(k = 0) \ \underline {= 0.01}$. |
| − | '''(4)''' | + | '''(4)''' In the GE model, the correlation duration is given as follows ($S$ stands for sum): |
:$$D_{\rm K} = {1}/{S}-1 \hspace{0.05cm},\hspace{0.2cm}S = {\rm | :$$D_{\rm K} = {1}/{S}-1 \hspace{0.05cm},\hspace{0.2cm}S = {\rm | ||
Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) + {\rm Pr}(\rm | Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) + {\rm Pr}(\rm | ||
B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$ | B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$ | ||
| − | * | + | *Further, using the data for Exercise 5.7: |
:$$q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G }) = \frac{\alpha_{\rm | :$$q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G }) = \frac{\alpha_{\rm | ||
B} \cdot S}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot | B} \cdot S}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot | ||
| Line 143: | Line 143: | ||
q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B })}-1 \hspace{0.05cm}.$$ | q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B })}-1 \hspace{0.05cm}.$$ | ||
| − | * | + | *So, the correct solution is <u>solution 2</u>. With the given parameter values, we obtain, for example: |
:$$D_{\rm K} =\frac{1}{0.0061 \cdot 0.3724 + 0.1949 \cdot | :$$D_{\rm K} =\frac{1}{0.0061 \cdot 0.3724 + 0.1949 \cdot | ||
0.5528}-1=\frac{1}{0.11}-1 {\approx 8.09}\hspace{0.05cm}.$$ | 0.5528}-1=\frac{1}{0.11}-1 {\approx 8.09}\hspace{0.05cm}.$$ | ||
| − | * | + | *The result is exactly the same value as in subtask '''(3)''' of Exercise 5.6. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 10:22, 21 September 2022
As in "Exercise 5.6", "Exercise 5.6Z" and "Exercise 5.7", we consider the burst error channel model according to Gilbert and Elliott (GE model) with the parameters
- $$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, \hspace{0.2cm}p_{\rm B} = 0.1,\hspace{0.2cm} p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.1, \hspace{0.2cm} p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$
From these four probabilities, the corresponding characteristics of the channel model according to McCullough (MC model) can be determined in such a way that both models have exactly the same statistical properties, namely
- exactly the same error distance distribution (EDD) $V_a(k)$,
- exactly the same error correlation function (ECF) $\varphi_e(k)$.
The probabilities of the MC model were determined in "Exercise 5.7" as follows $($labels according to the graph for Exercise 5.7, all with $q$ instead of $p)$:
- $$q_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.0061, \hspace{0.2cm}q_{\rm B} = 0.1949,\hspace{0.2cm} q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5528, \hspace{0.2cm} q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.3724\hspace{0.05cm}.$$
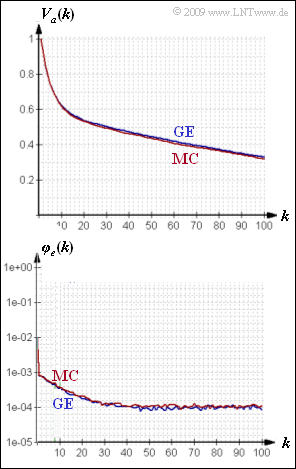
The upper graph shows the functions $V_a(k)$ and $\varphi_e(k)$ simulatively determined from $N = 10^6$ sequence elements for the GE and MC models. There are still slight discrepancies here. In the limiting case for $N → ∞$, on the other hand, error correlation function and error distance distribution of both models agree exactly.
In this exercise, important descriptive variables of the GE model such as
- state probabilities,
- mean error probabilities, and
- correlation duration
should be determined directly from the $q$ parameters of the MC model.
Notes:
- The exercise belongs to the chapter "Burst Error Channels".
- From the above exercises, the following results can be further used:
- (a) The state probabilities of the GE model are
- $$w_{\rm G} = \frac{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 - w_{\rm G }\hspace{0.05cm}.$$
- (b) The mean error probability of the GE model is
- $$p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} = \varphi_{e}(k = 0 )\hspace{0.05cm}.$$
- (c) The correlation duration of the GE model is calculated as
- $$D_{\rm K} =\frac{1}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )}-1 \hspace{0.05cm}.$$
Questions
Solution
- $$w_{\rm G} = \frac{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = 0.909 \hspace{0.05cm},\hspace{0.5cm} w_{\rm B} = 1 - w_{\rm G }= 0.091\hspace{0.05cm}.$$
- In contrast, for the MC model we obtain:
- $$\alpha_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}= \frac{0.5528}{0.5528 + 0.3724}\hspace{0.15cm}\underline {= 0.5975}\hspace{0.05cm},\hspace{0.5cm} \alpha_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 - \alpha_{\rm G} \hspace{0.15cm}\underline {= 0.4025}\hspace{0.05cm}.$$
- In subtask (3) of Exercise 5.7, these values have already been determined once, but from the parameters of the equivalent Gilbert-Elliott model.
(2) The mean error distance in the channel state "GOOD" is equal to the reciprocal of the associated error probability $q_{\rm G}$.
- Accordingly, the mean error distance in the state "BAD" is $1/q_{\rm B}$.
- By weighting with the two state probabilities $\alpha_{\rm G}$ and $\alpha_{\rm B}$, the mean error distance of the MC model as a whole is given by
- $${\rm E}[a] =\frac{\alpha_{\rm G}}{q_{\rm G}} + \frac{\alpha_{\rm B}}{q_{\rm B}}=\frac{0.5975}{0.0061} + \frac{0.4025}{0.1949} = 97.95 + 2.06\hspace{0.15cm}\underline { = 100.1}\hspace{0.05cm}.$$
- Of course, this value should be exactly the same as for the corresponding GE model.
- The small deviation of $0.1$ is due to rounding errors.
(3) Again, the relation $\varphi_e(k = 0) = p_{\rm M}$ holds.
- However, the mean error probability is equal to the reciprocal of the mean error distance ${\rm E}[a]$.
- It follows that $\varphi_e(k = 0) \ \underline {= 0.01}$.
(4) In the GE model, the correlation duration is given as follows ($S$ stands for sum):
- $$D_{\rm K} = {1}/{S}-1 \hspace{0.05cm},\hspace{0.2cm}S = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$
- Further, using the data for Exercise 5.7:
- $$q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G }) = \frac{\alpha_{\rm B} \cdot S}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot q_{\rm G}} \hspace{0.05cm}, \hspace{0.2cm}q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B })= \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )$$
- $$\Rightarrow \hspace{0.3cm} S = q_{\rm G} \cdot q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G }) + q_{\rm B} \cdot \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) = q_{\rm G} \cdot q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G })+ q_{\rm B} \cdot q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B }) \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm}D_{\rm K} =\frac{1}{q_{\rm G} \cdot q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G })+ q_{\rm B} \cdot q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B })}-1 \hspace{0.05cm}.$$
- So, the correct solution is solution 2. With the given parameter values, we obtain, for example:
- $$D_{\rm K} =\frac{1}{0.0061 \cdot 0.3724 + 0.1949 \cdot 0.5528}-1=\frac{1}{0.11}-1 {\approx 8.09}\hspace{0.05cm}.$$
- The result is exactly the same value as in subtask (3) of Exercise 5.6.