| Line 150: | Line 150: | ||
[[File:EN_KC_T_2_2_S1.png|right|frame|Übergang von ${\rm GF}(2)$ auf ${\rm GF}(2^2)$ |class=fit]] | [[File:EN_KC_T_2_2_S1.png|right|frame|Übergang von ${\rm GF}(2)$ auf ${\rm GF}(2^2)$ |class=fit]] | ||
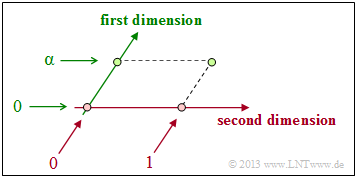
| − | + | But what is the meaning of the new element $\alpha$? | |
| − | * | + | *The polynomial $p(\alpha)= \alpha^2 + \alpha + 1 $ has no zero in ${\rm GF}(2) = \{0, \ 1\}$ . This further implies that $\alpha$ can be neither $0$ nor $1$ .<br> |
| − | * | + | *If $\alpha= 0$ resp. $\alpha= 1$, then moreover two of the four set elements $\{0,\ 1,\ \alpha,\ 1 + \alpha\}$ would be identical respectively: Either "$0$" and "$\alpha$" as well as "$1$" and "$1+\alpha$" or "$1$" and "$\alpha$" as well as "$0$" and "$1+\alpha$". |
| − | * | + | *Much more the one-dimensional field ${\rm GF}(2)$ gets a second dimension by the introduction of the element $\alpha$ . It is thus extended to the Galois field ${\rm GF}(2^2)$ as shown in the accompanying diagram. |
| − | * | + | *The element $\alpha$ has similar meaning as the imaginary unit ${\rm j}$, by which one extends the set of real numbers under the constraint ${\rm j}^2 + 1 = 0$ to the set of complex numbers. |
<br clear=all> | <br clear=all> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Common representation of the binary extension field}\ {\rm GF}(2^2)\text{:}$ |
| − | + | Due to the identity $\alpha^2 = 1 + \alpha$, which follows from the constraint $p(\alpha) = 0$ , one can write in the same way ${\rm GF}(2^2) = \{0,\ 1,\ \alpha,\ \alpha^2\}$ where now the following operation tables hold: | |
:$$ \begin{array}{c} | :$$ \begin{array}{c} | ||
| Line 184: | Line 184: | ||
| − | == | + | == Polynomials over a finite field == |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ A '''polynomial''' in a finite field ${\rm GF}(P)$, where $P$ denotes a prime number, has the following form: |
::<math>a(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_0 + a_1 \cdot x + a_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + a_m \cdot x^{m} | ::<math>a(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_0 + a_1 \cdot x + a_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + a_m \cdot x^{m} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | To note: | |
| − | * | + | *All coefficients $a_i $ are elements of the field: $a_i \in {\rm GF}(P)$.<br> |
| − | * | + | *If the leading coefficient $a_m ≠ 0$, then $m$ indicates the '''degree'''' of the polynomial.}}<br> |
| − | + | Let us consider a second polynomial with degree $M$, | |
::<math>b(x) = \sum_{i = 0}^{M} b_i \cdot x^{i} = b_0 + b_1 \cdot x + b_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + b_M \cdot x^{M} | ::<math>b(x) = \sum_{i = 0}^{M} b_i \cdot x^{i} = b_0 + b_1 \cdot x + b_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + b_M \cdot x^{M} | ||
\hspace{0.05cm},</math> | \hspace{0.05cm},</math> | ||
| − | + | then we get for the sum (resp. difference) and the product respectively in ${\rm GF}(P)$: | |
::<math>a(x) \pm b(x) = \sum_{i = 0}^{{\rm max}\hspace{0.05cm}(m, \hspace{0.05cm}M)} \hspace{0.15cm}(a_i \pm b_i) \cdot x^{i} \hspace{0.05cm},</math> | ::<math>a(x) \pm b(x) = \sum_{i = 0}^{{\rm max}\hspace{0.05cm}(m, \hspace{0.05cm}M)} \hspace{0.15cm}(a_i \pm b_i) \cdot x^{i} \hspace{0.05cm},</math> | ||
| Line 209: | Line 209: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ $a(x) = x^3 + x + 1$ and $b(x) = x^2 + x + 1$ are valid. |
| − | + | In the binary Galois field ⇒ ${\rm GF}(2)$ results according to the above equations for the sum, difference and product of the two polynomials: | |
::<math>s(x) = a(x) + b(x) = x^3 + x^2 \hspace{0.05cm}, </math> | ::<math>s(x) = a(x) + b(x) = x^3 + x^2 \hspace{0.05cm}, </math> | ||
| Line 219: | Line 219: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | With $a_0 = a_1 = a_3 = b_0 = b_1 =b_2 = 1$ und $a_2 = a_4 = a_5 = b_3 = b_4 =b_5 = 0$ we obtain: | |
::<math>c_0 = a_0 \cdot b_0 = 1 \cdot 1 = 1 \hspace{0.05cm},</math> | ::<math>c_0 = a_0 \cdot b_0 = 1 \cdot 1 = 1 \hspace{0.05cm},</math> | ||
| Line 233: | Line 233: | ||
::<math>\Rightarrow \hspace{0.3cm} c(x) = x^5 + x^4 +1 \hspace{0.05cm}.</math> | ::<math>\Rightarrow \hspace{0.3cm} c(x) = x^5 + x^4 +1 \hspace{0.05cm}.</math> | ||
| − | + | In the Galois field ${\rm GF}(3)$ other results are obtained due to the modulo 3 operations: | |
::<math>s(x) = (x^3 + x + 1) + (x^2 + x + 1) = x^3 + x^2 + 2x + 2\hspace{0.05cm},</math> | ::<math>s(x) = (x^3 + x + 1) + (x^2 + x + 1) = x^3 + x^2 + 2x + 2\hspace{0.05cm},</math> | ||
| Line 240: | Line 240: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ A polynomial $a(x)$ is called '''reducible''' if it can be represented as the product of two polynomials $p(x)$ and $q(x)$ each of lower degree: |
::<math>a(x) = p(x) \cdot q(x) | ::<math>a(x) = p(x) \cdot q(x) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | If this factorization is not possible, that is | |
::<math>a(x) = p(x) \cdot q(x) + r(x)\hspace{0.05cm},\hspace{0.5cm} r(x) \ne 0</math> | ::<math>a(x) = p(x) \cdot q(x) + r(x)\hspace{0.05cm},\hspace{0.5cm} r(x) \ne 0</math> | ||
| − | + | holds, then it is called an '''irreducible''' or '''prime''' polynomial}}<br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 2:}$ Es gelte $b(x) = x^3 + x + 1$, $p_1(x) = x^2 + x + 1$ und $p_2(x) = x^2 + 1$. | $\text{Beispiel 2:}$ Es gelte $b(x) = x^3 + x + 1$, $p_1(x) = x^2 + x + 1$ und $p_2(x) = x^2 + 1$. | ||
| − | + | The graph on the left illustrates the modulo 2 multiplication $a(x)= b(x) \cdot p_1(x)$. The result is $a(x) = x^5 + x^4 + 1$.<br> | |
| − | [[File:EN_KC_T_2_2_S2.png|center|frame| | + | [[File:EN_KC_T_2_2_S2.png|center|frame|Example of polynomial multiplication and division|class=fit]] |
| − | + | In the right part of the above graph, the modulo 2 division $q(x)= a(x)/ p_2(x)$ is shown with the result $q(x) = x^3 + x^2 + x + 1$ . This leaves the remainder $r(x) = x$. According to this calculation alone $a(x) = x^5 + x^4 + 1$ could well be an irreducible polynomial.<br> | |
| − | + | However, the proof that the polynomial $a(x) = x^5 + x^4 + 1$ is indeed irreducible would only be given if $a(x)/p(x)$ yields a remainder for all | |
| − | ::<math>p(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}\text{...} \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}</math> | + | ::<math>p(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}\text{...} \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}.</math> |
| − | + | This would require (almost) $2^5 = 32$ divisions in the present example.<br> | |
| − | + | Based on our left-hand calculation, we can immediately see here that $a(x)$ is certainly not an irreducible polynomial, since, for example, $a(x) = x^5 + x^4 + 1$ divided by $p_1(x) = x^2 + x + 1$ yields the polynomial $b(x) = x^3 + x + 1$ with no remainder.}}<br> | |
== Verallgemeinerte Definition eines Erweiterungskörpers == | == Verallgemeinerte Definition eines Erweiterungskörpers == | ||
Revision as of 23:27, 30 August 2022
Contents
GF(22) – Example of extension fields
In the section $\text{"Example 2"}$ in the chapter "Some Basics of Algebra" it has already been shown that the finite set of numbers $\{0, 1, 2, 3\}$ ⇒ $q = 4$ does not satisfy the properties of a Galois field $\rm GF(4)$ . Rather, the following tables result for the addition modulo 4 and the multiplication modulo 4:
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm}{\it q} = 4\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm}\text{Addition: } \left[ \begin{array}{c|cccccc} + & 0 & 1 &2 & 3 \\ \hline 0 & 0 & 1 &2 & 3 \\ 1 & 1 & 2 &3 & 0 \\ 2 & 2 & 3 &0 & 1 \\ 3 & 3 & 0 &1 & 2 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.25cm}\text{Multiplication: } \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 &2 & 3 \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 2 & 3 \\ 2 & 0 & 2 & 0 & 2 \\ 3 & 0 & 3 & 2 & 1 \\ \end{array} \right] . $$
For $z_i = 2$ there is no multiplicative inverse ${\rm Inv_M}(z_i)$. This can be seen from the fact that no single element $z_i ∈ \{0, 1, 2, 3\}$ satisfies the condition $2 · z_i = 1$ .
On the other hand, if we start from the binary Galois field ${\rm GF}(2) = \{0, 1\}$ and extend it according to the equation
- \[{\rm GF}(2^2)= \big\{k_0+k_1\cdot \alpha \ \big | \ k_0, k_1\in{\rm GF}(2) = \{ 0, 1\} \big \}\hspace{0.05cm}, \]
then the likewise finite set' $\{0, 1, \alpha, 1 + \alpha\}$ ⇒ order is further $q=4$.
Performing the arithmetic operations modulo $p(\alpha) = \alpha^2 + \alpha + 1$ we get the following result:
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm}{\it p}(\alpha)= \alpha^2 + \alpha + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c|cccccc} + & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 1 & \alpha & 1\!+\!\alpha \\ 1 & 1 & 0 & 1\!+\!\alpha & \alpha \\ \alpha & \alpha & 1\!+\!\alpha & 0 & 1 \\ 1\!+\!\alpha & 1\!+\!\alpha & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & 1\!+\!\alpha \\ \alpha & 0 & \alpha & 1\!+\!\alpha & 1 \\ 1\!+\!\alpha & 0 & 1\!+\!\alpha & 1 & \alpha \end{array} \right] .$$
In this regard, it should be noted:
- The neutral elements of addition or multiplication are still $N_{\rm A} = 0$ and $N_{\rm M} = 1$.
- Since there is no difference between addition and subtraction in modulo arithmetic $\alpha + \alpha = \alpha - \alpha = 0$.
- For all $z_i$ thus holds: The additive inverse of $z_i$ is the element $z_i$ itself.
- The entries in the multiplication table are obtained according to the following calculations:
- \[\big [ \alpha \cdot (1+\alpha) \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) = (\alpha^2 + \alpha) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= 1\hspace{0.05cm},\]
- \[\big [ \alpha \cdot \alpha \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) = (\alpha^2 ) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= 1+\alpha\hspace{0.05cm},\]
- \[\big [ (1+\alpha) \cdot (1+\alpha) \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) = (\alpha^2 + 1) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= \alpha\hspace{0.05cm}.\]
- Thus, the multiplicative inverses exist for all elements except the zero element:
- \[{\rm Inv_M}( 1) = 1 \hspace{0.05cm},\hspace{0.2cm}{\rm Inv_M}(\alpha) = 1+\alpha \hspace{0.05cm},\hspace{0.2cm}{\rm Inv_M}(1+\alpha) = \alpha \hspace{0.05cm}.\]
$\text{Intermediate result:}$
- The set $\{0, \ 1, \ \alpha, \ 1 + \alpha\}$ together with the two operations addition and multiplication modulo $p(\alpha)= \alpha^2 + \alpha + 1$ represents a Galois field. The order is $q = 4$.
- This Galois field, denoted by $\rm GF(2^2) = GF(4)$ satisfies all the requirements mentioned in thr "previous chapter" .
- In contrast to the Galois field $\rm GF(3) = \{0, \ 1, \ 2\}$ with the property that $q = 3$ is a prime number, $\rm GF(2^2)$ is called an extension field.
Reducible and irreducible polynomials
The polynomial $p(\alpha)$ and thus the equation of determination $p(\alpha) = 0$ must not be given arbitrarily. The polynomial used on the last page
- $$p(\alpha)= \alpha^2 + \alpha + 1$$
is suitable. Now we try another polynomial, namely $p(\alpha)= \alpha^2 + 1$.
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm}{\it p}(\alpha)= \alpha^2 + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c|cccccc} + & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 1 & \alpha & 1\!+\!\alpha \\ 1 & 1 & 0 & 1\!+\!\alpha & \alpha \\ \alpha & \alpha & 1\!+\!\alpha & 0 & 1 \\ 1\!+\!\alpha & 1\!+\!\alpha & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & 1\!+\!\alpha \\ \alpha & 0 & \alpha & 1 &1\!+\!\alpha \\ 1\!+\!\alpha & 0 & 1\!+\!\alpha & 1\!+\!\alpha & 0 \end{array} \right] .$$
The addition table is identical in both cases and also the multiplication tables differ only by the four entries in the two bottom rows and the two last columns:
- From $p(\alpha) = 0$ now follows for the product $\alpha \cdot \alpha = 1$ and the product $(1 +\alpha) \cdot (1 +\alpha) $ gives the zero element. The mixed product is $\alpha \cdot (1 +\alpha) = 1 +\alpha $.
- In the last row of the multiplication table and also in the last column there is now no "$1$" ⇒ Concerning the condition $p(\alpha)= \alpha^2 + 1= 0$ consequently the multiplicative inverse to $1 +\alpha$ does not exist.
- But thus the finite set $\{0, \ 1, \ \alpha, \ 1 + \alpha\}$ together with arithmetic operations modulo $p(\alpha)= \alpha^2 + 1$ does not satisfy the conditions of an extension fields either $\rm GF(2^2) $.
$\text{Let us summarize:}$
From the binary Galois field $\rm GF(2) = \{0, \ 1\}$ an extension field $\rm GF(2^2)$ can be formulated with the aid of a polynomial of degree $m = 2$ with binary coefficients:
- \[p(x) = x^2 + k_1 \cdot x + k_0 \hspace{0.05cm}, \hspace{0.45cm}k_0\hspace{0.05cm},\hspace{0.1cm}k_1 \in \{0, 1\} \hspace{0.05cm}.\]
Note: The renaming of the variable $\alpha$ to $x$ has only formal meaning with regard to later pages.
- In the present case there is only one suitable polynomial $p_1(x)= x^2 + x + 1$. All other possible polynomials of degree $m = 2$, namely,
- \[p_2(x) = x^2 + 1 \hspace{0.06cm} = (x+1) \cdot (x+1)\hspace{0.05cm},\]
- \[p_3(x) =x^2 \hspace{0.76cm} = x \cdot x \hspace{0.05cm},\]
- \[p_4(x) = x^2 + x = (x+1) \cdot x\hspace{0.05cm}, \]
- can be factorized and do not yield extension fields.
- The polynomials $p_2(x)$, $p_3(x)$ and $p_4(x)$ are called reducible.
- The conclusion is obvious that only irreducible polynomials such as $p_1(x)$ are suitable for an extension fields
.
Interpretation of the new element "alpha
We further consider the field ${\rm GF}(2^2) = \{0, \ 1,\ \alpha,\ 1 + \alpha\}$ corresponding to the following two operational tables, based on the constraint $p(\alpha)= \alpha^2 + \alpha + 1 = 0$ (irreducible ploynomial):
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm} p(\alpha)= \alpha^2 + \alpha + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c|cccccc} + & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 1 & \alpha & 1\!+\!\alpha \\ 1 & 1 & 0 & 1\!+\!\alpha & \alpha \\ \alpha & \alpha & 1\!+\!\alpha & 0 & 1 \\ 1\!+\!\alpha & 1\!+\!\alpha & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & 1\!+\!\alpha \\ \alpha & 0 & \alpha & 1\!+\!\alpha & 1 \\ 1\!+\!\alpha & 0 & 1\!+\!\alpha & 1 & \alpha \end{array} \right] .$$
But what is the meaning of the new element $\alpha$?
- The polynomial $p(\alpha)= \alpha^2 + \alpha + 1 $ has no zero in ${\rm GF}(2) = \{0, \ 1\}$ . This further implies that $\alpha$ can be neither $0$ nor $1$ .
- If $\alpha= 0$ resp. $\alpha= 1$, then moreover two of the four set elements $\{0,\ 1,\ \alpha,\ 1 + \alpha\}$ would be identical respectively: Either "$0$" and "$\alpha$" as well as "$1$" and "$1+\alpha$" or "$1$" and "$\alpha$" as well as "$0$" and "$1+\alpha$".
- Much more the one-dimensional field ${\rm GF}(2)$ gets a second dimension by the introduction of the element $\alpha$ . It is thus extended to the Galois field ${\rm GF}(2^2)$ as shown in the accompanying diagram.
- The element $\alpha$ has similar meaning as the imaginary unit ${\rm j}$, by which one extends the set of real numbers under the constraint ${\rm j}^2 + 1 = 0$ to the set of complex numbers.
$\text{Common representation of the binary extension field}\ {\rm GF}(2^2)\text{:}$
Due to the identity $\alpha^2 = 1 + \alpha$, which follows from the constraint $p(\alpha) = 0$ , one can write in the same way ${\rm GF}(2^2) = \{0,\ 1,\ \alpha,\ \alpha^2\}$ where now the following operation tables hold:
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm} p(\alpha)= \alpha^2 + \alpha + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c | cccccc} + & 0 & 1 & \alpha & \alpha^2 \\ \hline 0 & 0 & 1 & \alpha & \alpha^2 \\ 1 & 1 & 0 & \alpha^2 & \alpha \\ \alpha & \alpha & \alpha^2 & 0 & 1 \\ \alpha^2 & \alpha^2 & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c | cccccc} \cdot & 0 & 1 & \alpha & \alpha^2 \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & \alpha^2 \\ \alpha & 0 & \alpha &\alpha^2 & 1 \\ \alpha^2 & 0 & \alpha^2 & 1 & \alpha \end{array} \right] .$$
Polynomials over a finite field
$\text{Definition:}$ A polynomial in a finite field ${\rm GF}(P)$, where $P$ denotes a prime number, has the following form:
- \[a(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_0 + a_1 \cdot x + a_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + a_m \cdot x^{m} \hspace{0.05cm}.\]
To note:
- All coefficients $a_i $ are elements of the field: $a_i \in {\rm GF}(P)$.
- If the leading coefficient $a_m ≠ 0$, then $m$ indicates the degree' of the polynomial.
Let us consider a second polynomial with degree $M$,
- \[b(x) = \sum_{i = 0}^{M} b_i \cdot x^{i} = b_0 + b_1 \cdot x + b_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + b_M \cdot x^{M} \hspace{0.05cm},\]
then we get for the sum (resp. difference) and the product respectively in ${\rm GF}(P)$:
- \[a(x) \pm b(x) = \sum_{i = 0}^{{\rm max}\hspace{0.05cm}(m, \hspace{0.05cm}M)} \hspace{0.15cm}(a_i \pm b_i) \cdot x^{i} \hspace{0.05cm},\]
- \[a(x) \cdot b(x) = \sum_{i = 0}^{m + M} \hspace{0.15cm}c_i \cdot x^{i}\hspace{0.05cm},\hspace{0.5cm} c_i = \sum_{j = 0}^{i}\hspace{0.15cm}a_j \cdot b_{i-j} \hspace{0.05cm}.\]
$\text{Example 1:}$ $a(x) = x^3 + x + 1$ and $b(x) = x^2 + x + 1$ are valid.
In the binary Galois field ⇒ ${\rm GF}(2)$ results according to the above equations for the sum, difference and product of the two polynomials:
- \[s(x) = a(x) + b(x) = x^3 + x^2 \hspace{0.05cm}, \]
- \[d(x) = a(x) - b(x) = x^3 + x^2 = s(x)\hspace{0.05cm},\]
- \[c(x) = a(x) \cdot b(x) =\sum_{i = 0}^{3 + 2} \hspace{0.15cm}c_i \cdot x^{i}\hspace{0.05cm},\hspace{0.5cm} c_i = \sum_{j = 0}^{i}\hspace{0.15cm}a_j \cdot b_{i-j} \hspace{0.05cm}.\]
With $a_0 = a_1 = a_3 = b_0 = b_1 =b_2 = 1$ und $a_2 = a_4 = a_5 = b_3 = b_4 =b_5 = 0$ we obtain:
- \[c_0 = a_0 \cdot b_0 = 1 \cdot 1 = 1 \hspace{0.05cm},\]
- \[c_1 = a_0 \cdot b_1 + a_1 \cdot b_0 = 1 \cdot 1 + 1 \cdot 1 = 0 \hspace{0.05cm},\]
- \[c_2 =a_0 \cdot b_2 + a_1 \cdot b_1 + a_2 \cdot b_0 = 1 \cdot 1 + 1 \cdot 1 + 0 \cdot 1 = 0 \hspace{0.05cm},\]
- \[c_3 = a_0 \cdot b_3 + a_1 \cdot b_2 + a_2 \cdot b_1 + a_3 \cdot b_0 = 1 \cdot 0 + 1 \cdot 1 + 0 \cdot 1 + 1 \cdot 1 = 0 \hspace{0.05cm},\]
- \[c_4=a_0 \cdot b_4 + a_1 \cdot b_3 + \hspace{0.05cm}\text{...}\hspace{0.05cm}+ \hspace{0.05cm}a_4 \cdot b_0 =1 \cdot 0 + 1 \cdot 0 + 0 \cdot 1 + 1 \cdot 1 + 0 \cdot 1 = 1 \hspace{0.05cm},\]
- \[c_5 = a_0 \cdot b_5 + a_1 \cdot b_4 + \hspace{0.05cm}\text{...}\hspace{0.05cm}+ \hspace{0.05cm} a_5 \cdot b_0 =1 \cdot 0 + 1 \cdot 0 + 0 \cdot 0 + 1 \cdot 1 + 0 \cdot 1 + 0 \cdot 1= 1 \]
- \[\Rightarrow \hspace{0.3cm} c(x) = x^5 + x^4 +1 \hspace{0.05cm}.\]
In the Galois field ${\rm GF}(3)$ other results are obtained due to the modulo 3 operations:
- \[s(x) = (x^3 + x + 1) + (x^2 + x + 1) = x^3 + x^2 + 2x + 2\hspace{0.05cm},\]
- \[d(x) = (x^3 + x + 1) - (x^2 + x + 1) = x^3 + 2x^2 \hspace{0.05cm},\]
- \[c(x) = (x^3 + x + 1) \cdot (x^2 + x + 1) = x^5 + x^4 + 2x^3 + 2x^2 + 2x +1\hspace{0.05cm}.\]
$\text{Definition:}$ A polynomial $a(x)$ is called reducible if it can be represented as the product of two polynomials $p(x)$ and $q(x)$ each of lower degree:
- \[a(x) = p(x) \cdot q(x) \hspace{0.05cm}.\]
If this factorization is not possible, that is
- \[a(x) = p(x) \cdot q(x) + r(x)\hspace{0.05cm},\hspace{0.5cm} r(x) \ne 0\]
holds, then it is called an irreducible or prime polynomial
$\text{Beispiel 2:}$ Es gelte $b(x) = x^3 + x + 1$, $p_1(x) = x^2 + x + 1$ und $p_2(x) = x^2 + 1$.
The graph on the left illustrates the modulo 2 multiplication $a(x)= b(x) \cdot p_1(x)$. The result is $a(x) = x^5 + x^4 + 1$.
In the right part of the above graph, the modulo 2 division $q(x)= a(x)/ p_2(x)$ is shown with the result $q(x) = x^3 + x^2 + x + 1$ . This leaves the remainder $r(x) = x$. According to this calculation alone $a(x) = x^5 + x^4 + 1$ could well be an irreducible polynomial.
However, the proof that the polynomial $a(x) = x^5 + x^4 + 1$ is indeed irreducible would only be given if $a(x)/p(x)$ yields a remainder for all
- \[p(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}\text{...} \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}.\]
This would require (almost) $2^5 = 32$ divisions in the present example.
Based on our left-hand calculation, we can immediately see here that $a(x)$ is certainly not an irreducible polynomial, since, for example, $a(x) = x^5 + x^4 + 1$ divided by $p_1(x) = x^2 + x + 1$ yields the polynomial $b(x) = x^3 + x + 1$ with no remainder.
Verallgemeinerte Definition eines Erweiterungskörpers
Wir gehen von folgenden Voraussetzungen aus:
- einem Galoisfeld ${\rm GF}(P)$, wobei $P$ eine Primzahl angibt,
- einem irreduziblen Polynom $p(x)$ über ${\rm GF}(P)$ vom Grad $m$:
- \[p(x) = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}\text{...} \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}, \hspace{0.3cm} a_i \in {\rm G}(P)\hspace{0.05cm}, \hspace{0.15cm}a_m \ne 0\hspace{0.05cm}. \]
Mit den genannten Voraussetzungen gilt allgemein:
$\text{Definition:}$ Es sei $P$ eine Primzahl, $m$ ganzzahlig, $p(x)$ ein irreduzibles Polynom vom Grad $m$ und es gelte $p(\alpha) = 0$.
Ein Erweiterungskörper lässt sich dann wie folgt beschreiben.
- \[{\rm GF}(P^m)= \Big\{ k_{m-1} \hspace{0.01cm}\cdot \hspace{0.02cm}\alpha^{m-1} \hspace{0.05cm}+ \hspace{0.05cm}\text{...} \hspace{0.05cm}+ \hspace{0.05cm}k_1 \hspace{0.01cm}\cdot \hspace{0.02cm} \alpha \hspace{0.05cm}+ \hspace{0.05cm} k_0\hspace{0.05cm} \Big{\vert}\hspace{0.02cm} \ k_i\in{\rm GF}(P) = \{ 0, 1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, P-1\}\Big \}.\]
- Die Addition und Multiplikation in diesem Erweiterungskörper entspricht dann der Polynom–Addition und Polynom–Multiplikation modulo $p(\alpha)$.
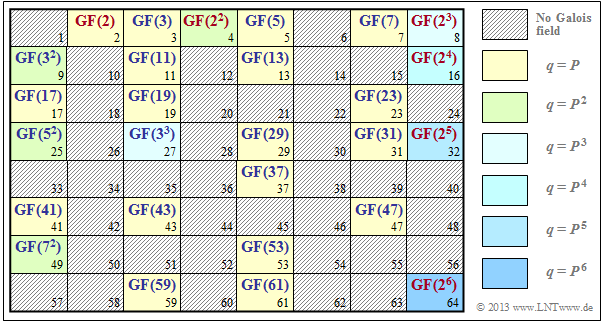
- Ein Galoisfeld ${\rm GF}(q)$ mit $q$ Elementen lässt sich also immer dann angeben, wenn die Elementenanzahl in der Form $q = P^m$ geschrieben werden kann
$(P$ kennzeichnet eine Primzahl, $m$ sei ganzzahlig$)$.
Die Grafik zeigt, für welche $q$–Werte sich jeweils ein Galoisfeld konstruieren lässt. Für die schraffiert eingezeichneten Werte ist kein endlicher Körper angebbar.
Weiter ist anzumerken:
- Die gelb hinterlegten Positionen $q=P$ ⇒ $m = 1$ markieren Zahlenmengen $\{0,\ 1,\hspace{0.05cm}\text{ ...} \hspace{0.05cm},\ q- 1\}$ mit Galoiseigenschaften, siehe Seite Definition eines Galoisfeldes.
- Die anderen Hinterlegungsfarben markieren Erweiterungskörper mit $q=P^m$, $m ≥ 2$. Für $q ≤ 64$ basieren diese auf den Primzahlen $2$, $3$, $5$ und $7$.
- Mit roter Schrift hervorgehoben sind binäre Körper ⇒ $q=2^m$, $m ≥ 1$, die auf der nächsten Seite noch genauer betrachtet werden. Alle anderen Erweiterungskörper sind blau beschriftet.
Binäre Erweiterungskörper – Primitive Polynome
Im Folgenden betrachten wir binäre Erweiterungskörper mit
- \[q = 2^m \hspace{0.15cm}(m \ge 2) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} q = 4,\ 8,\ 16, 32,\ 64,\ \text{...}\]
Elementen.
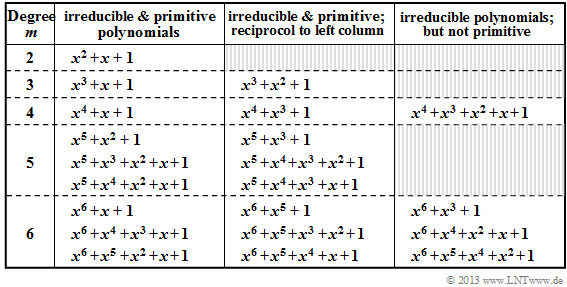
- In der Tabelle sind für $2 ≤ m ≤ 6$ alle irreduziblen Polynome des Galoisfeldes ${\rm GF}(2)$ angegeben.
- Die Polynome in Spalte 2 und 3 sind nicht nur irreduzibel, sondern zusätzlich auch primitiv.
- Primitive Polynome liefern auch die Grundlage für die Realisierung von Pseudo–Noise–Generatoren.
Bevor wir uns der Definition eines primitiven Polynoms zuwenden, sollen zunächst die Besonderheiten "primitiver Elemente" am Beispiel von
- \[{\rm GF}(q) = \{\hspace{0.05cm}z_0 = 0,\hspace{0.1cm} z_1 = 1,\hspace{0.05cm} \text{...}\hspace{0.05cm} , \hspace{0.05cm}z_{q-1}\}\]
genannt werden. Das Element $z_i = \beta$ wird dann als primitiv bezeichnet,
- wenn die Potenz $\beta^{\hspace{0.05cm}i}$ modulo $q$ zum ersten Mal für $i = q-1$ zum Ergebnis "$1$" führt, so dass
- $\beta^{\hspace{0.05cm}i}$ für $1 ≤ i ≤ q- 1$ genau die Elemente $z_1$, ... , $z_{q-1}$ liefert, also alle Elemente von ${\rm GF}(q)$ mit Ausnahme des Nullelementes $z_0 = 0$.
$\text{Beispiel 3:}$ Von der Zahlenmenge $Z_5 = \{0,\ 1,\ 2,\ 3,\ 4\}$ sind "$2$" und "$3$" primitive Elemente wegen
- \[2^1 \hspace{-0.1cm} = \hspace{-0.1cm} 2\hspace{0.05cm},\hspace{0.2cm} 2^2 = 4\hspace{0.05cm},\hspace{0.2cm} 2^3 = 8 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},\hspace{0.2cm} 2^4 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},\]
- \[3^1 \hspace{-0.1cm} = \hspace{-0.1cm} 3\hspace{0.05cm},\hspace{0.2cm} 3^2 = 9\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 3^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} 3^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\]
- Dagegen ist "$4$" kein primitives Element, weil bereits" $4^2 = 1$" ist:
- \[4^1 = 4\hspace{0.05cm},\hspace{0.2cm} 4^2 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},\hspace{0.2cm} 4^3 = 64 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 4^4 = 256 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm}.\]
$\text{Definition:}$ Ein irreduzibles Polynom bezeichnet man gleichzeitig als ein primitives Polynom, wenn die Wurzel $\alpha$ bezüglich des Polynoms $p(x)$ ein primitives Element von ${\rm GF}(q)$ ist. Dann gilt
- \[{\rm GF}(q) = \{\hspace{0.1cm}\alpha^{-\infty} = 0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} = 1,\hspace{0.05cm}\hspace{0.2cm} \alpha\hspace{0.05cm},\hspace{0.2cm} \alpha^{2},\hspace{0.2cm} \text{...} \hspace{0.1cm} , \hspace{0.2cm}\alpha^{q-2}\hspace{0.1cm}\}\hspace{0.05cm}. \]
- Alle in Spalte 2 der obigen Tabelle angegebenen Polynome sind sowohl irreduzibel als auch primitiv.
- Ist $p_1(x)$ ein primitives Polynom, so ist auch das dazu reziproke Polynom $p_2 (x) = x^m \cdot p_1(x^{-1})$ primitiv.
- Alle Polynome in Spalte 3 sind reziprok zum Polynom in Spalte 2. Beispielsweise gilt für $m = 3$:
- \[p_1(x) = x^3 + x + 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}p_2(x) = x^3 \cdot \big[x^{-3} + x^{-1} + 1 \big]= x^3 + x^2 + 1 \hspace{0.05cm}.\]
- Die irreduziblen Polynome der Spalte 4 sind dagegen nicht primitiv; sie spielen nur eine untergeordnete Rolle zur Beschreibung von Fehlerkorrekturverfahren.
$\text{Beispiel 4:}$ Zur Verdeutlichung dieser Aussagen betrachten wir beispielhaft
- das Galoisfeld $\rm GF(2^3) = GF(8)$, sowie
- das Polynom $p(x) = x^3 + x + 1$.
Aus der Bedingung $p(\alpha) = 0$ erhält man in $\rm GF(2^3)$ weiter:
- \[\alpha^3 + \alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\alpha^3 = \alpha + 1 \hspace{0.05cm},\]
und damit für die Potenzen $\alpha^{i}$ der Wurzel für $i ≥ 4$:
- \[\alpha^4 = \alpha \cdot \alpha^3 = \alpha \cdot (\alpha + 1) = \alpha^2 + \alpha \hspace{0.05cm},\]
- \[\alpha^5 = \alpha^2 \cdot \alpha^3 = \alpha^2 \cdot (\alpha + 1) = \alpha^3 + \alpha^2 = \alpha^2 + \alpha + 1 \hspace{0.05cm},\]
- \[\alpha^6 = \alpha^3 \cdot \alpha^3 = (\alpha + 1) \cdot (\alpha + 1) = \alpha^2 + \alpha + \alpha + 1= \alpha^2 + 1 \hspace{0.05cm},\]
- \[\alpha^7 = \alpha^4 \cdot \alpha^3 = (\alpha^2 + \alpha) \cdot (\alpha + 1) = \alpha^3 + \alpha^2 + \alpha^2 + \alpha = \alpha + 1 + \alpha = 1 = \alpha^0 \hspace{0.05cm}.\]
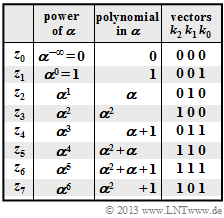
$\text{Beispiel 5:}$ Die Elemente $z_0$, $z_1$, ... , $z_7$ des Galoisfeldes $\rm GF(2^3)$ lassen sich entsprechend der nebenstehenden Tabelle wie folgt darstellen:
- als Potenzen von $\alpha$ ⇒ Exponentendarstellung,
- als Polynome der Form $k_2 \cdot \alpha^2 + k_1 \cdot \alpha + k_0$ mit binären Koeffizienten $k_2$, $k_1$, $k_0$ ⇒ Polynomdarstellung,
- als Vektoren der Koeffizienten $(k_2, \ k_1, \ k_0)$ ⇒ Koeffizientendarstellung.
Für Addition (oder Subtraktion) zweier Elemente eignen sich Polynom– und Vektordarstellung gleichermaßen, wobei die Komponenten $\text{modulo 2}$ zu addieren sind, zum Beispiel:
- \[z_5 + z_7 =(\alpha^2 + \alpha) + (\alpha^2 + 1) = \alpha + 1 = \alpha^3 = z_4 \hspace{0.05cm},\]
- \[{\rm oder}\hspace{0.15cm} z_5 + z_7 =(110) + (101) = (011) = z_4 \hspace{0.05cm},\]
- \[\hspace{0.15cm} z_1 + z_2 + z_3 =(001) + (010) + (100)= (111) = z_6 \hspace{0.05cm}.\]
Für Multiplikationen ist die Exponentendarstellung gut geeignet, wie folgende Beispiele zeigen:
- \[z_3 \cdot z_4 =\alpha^2 \cdot \alpha^3 = \alpha^{2+3}= \alpha^{5} = z_6 \hspace{0.05cm},\]
- \[z_0 \cdot z_5 =\alpha^{-\infty} \cdot \alpha^4 = \alpha^{-\infty} = z_0 \hspace{0.05cm},\]
- \[z_5 \cdot z_7 = \alpha^4 \cdot \alpha^6 = \alpha^{10}= \alpha^{7} \cdot \alpha^{3} = 1 \cdot \alpha^{3}= z_4 \hspace{0.05cm}.\]
Man erkennt, dass sich die Exponenten modulo $q-1$ ergeben $($im Beispiel modulo $7)$.
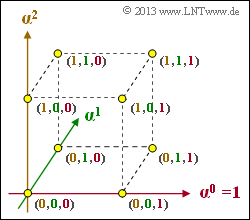
Die untere Grafik zeigt den endlichen Erweiterungskörper $\rm GF(2^3)$ in einer 3D–Darstellung:
- Die Achsen sind mit $\alpha^0 =1$, $\alpha^1$ und $\alpha^2$ bezeichnet.
- Die $2^3 = 8$ Punkte im 3D–Raum sind mit den Koeffizientenvektoren beschriftet.
- Die Zuordnung der Koeffizienten $k_2$, $k_1$, $k_0$ zu den Achsen ist farblich deutlich gemacht.
Aufgaben zum Kapitel
Aufgabe 2.3: Reduzible und irreduzible Polynome
Aufgabe 2.4: $\rm GF(2^2)$–Darstellungsformen
Aufgabe 2.4Z: Endliche und unendliche Körper
Aufgabe 2.5: Drei Varianten von $\rm GF(2^4)$
Aufgabe 2.5Z: Einige Berechnungen über $\rm GF(2^3)$
Aufgabe 2.6: ${\rm GF}(P^m)$. Welches $P$, welches $m$?